МАТЕМАТИЧЕСКОЕ сопровождение вычисления погрешностей при контроле наружнОго диаметра кольца подшипников после операции шлифования

Ларина Татьяна Вадимовна

студент 2 курса, автомеханический факультет ВПИ (филиал) ВолгГТУ, г. Волжский

Е-mail: 

Ребро Ирина Викторовна

научный руководитель, канд. пед. наук, доцент кафедры «Математика» ВПИ (филиал) ВолгГТУ, г. Волжский

Е-mail: 

.

Мустафина Джамиля Алиевна

научный руководитель, канд. пед. наук, доцент кафедры «Математика» ВПИ (филиал) ВолгГТУ, г. Волжский

Е-mail: dzamilyam@mail.ru

Применение статистических методов на современном этапе производства является необходимым многофункциональным инструментом, который характеризует концепцию качества продукции, соответствующего требованиям стандарта при определенной стабильности производственных процессов.

По мере совершенствования концепций качества изобретались новые подходы, критерии оценки, методологии и т. п., но в развитии реализовывался накопительный принцип — не отказываться от ранее созданного. Сегодня статистический метод оценки качества преобразовался в методологию шести сигм. Это значит, что обеспечивается такая стабильность производства, в которой количество несоответствий возможно на уровне 34 от 10 000 000 (при выпуске десяти миллионов изделий из них бракованных может быть 34) [1].

Технический прогресс, производство машин и приборов с высокими показателями точности, надежности и долговечности невозможны без изучения и усовершенствования методов и способов нахождения значений физической величины опытным путем, о чем написано в соответствующем ГОСТе 16263-70 «Государственная система обеспечения единства измерений. Метрология».

В приборах, используемых на производстве и при проведении эксперимента, измеряемые параметры отклоняются от идеальных значений вследствие: технологического разброса физических параметров исходных материалов и рассеивания геометрических размеров деталей при их изготовлении; измерения внешних условий; измерения режима работы электрических и пневматических источников; износа и старения материалов в процессе хранения и эксплуатации. Погрешности измерительных средств являются в большинстве случаев основными составляющими, оказывающими доминирующее влияние на суммарную погрешность измерения. На большинство измерительных средств разработаны стандарты или технические условия, в которых нормируются погрешности прибора (ГОСТ 8.051-73). Правильным методом нормирования является выделение систематической и случайной составляющих погрешность.

Основное требование, предъявляемое к расчёту, заключается в том, чтобы проводимые вычисления не вносили в результат дополнительной погрешности. При использовании в расчёте вычислительной техники это требование обычно выполняется, однако окончательный результат и его абсолютная погрешность содержат много цифр. Запись приближённых чисел с излишне большим количеством знаков создаёт лишь иллюзию высокой точности. При окончательной записи результата необходимо руководствоваться следующими правилами: абсолютную погрешность следует округлить до одной значащей цифры; результат округлить так, чтобы его последняя цифра находилась в том же разряде, что и единственная значащая цифра погрешности; общий десятичный множитель результата и погрешности вынести за скобки.

Приборная погрешность имеет высокую доверительную вероятность, приближающуюся к единице. Один из возможных способов оценки суммарной погрешности в этом случае заключается в следующем. Величина Δx_пр примерно соответствует «трёхсигмовому» интервалу. Доверительный интервал для используемой нами надёжности результата 0,95 равен «двухсигмовому», то есть он составляет ·Δx_пр. Тогда общая погрешность прямого измерения имеет вид: 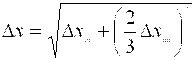. Следует иметь в виду, что складывать приборную

и случайную погрешности имеет смысл лишь в том случае, если они различаются меньше чем в три раза. Если же одна из погрешностей больше другой в три и более раз, её и следует принять в качестве меры общей погрешности.

Необходимость производства в точности измерений требуют правильного подхода к его оценке на современном уровне теории погрешностей. Наиболее точно определить величину абсолютной и относительной погрешности, с определенной надежностью, позволяет распределение Стьюдента. Например: «Проверка двух партий колец подвергшиеся шлифованию дала следующие результаты фактического отклонения действительного размера диаметра кольца от номинального:

·     первая партия x_i (мкм): 3,9; 4,1; 4,2; 4,4; 4,5; 4,7; 5,0; 5,1;

·     вторая партия y_i (мкм): 2,4; 2,8; 4,1; 4,4; 5,6; 6,8; 7,2; 8,9.

Для оценки точности измерения необходимо вычислить абсолютную и относительную погрешности, степень надежности ».

Вычисления для партии 1

Средний ожидаемый результат измерения: .

Среднеквадратическое отклонение:  .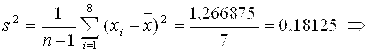

Среднеквадратичная погрешность результата измерений: , где .

Значение коэффициента Стьюдента  для надежности : .

Абсолютная погрешность:

Относительная погрешность: 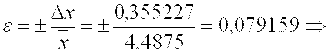 погрешность измерений составляет .

Общая погрешность прямого измерения в данном случае не считается.

Запишем доверительный интервал:

.

Вычисления для партии 2

Средний ожидаемый результат измерения: .

Среднеквадратическое отклонение:  .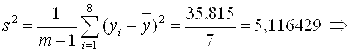

Среднеквадратичную погрешность результата измерений: , где

Абсолютная погрешность:

Относительная погрешность: 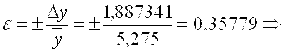 погрешность измерений составляет .

Общую погрешность прямого измерения в этом случае считать не надо.

Запишем доверительный интервал:

 .

Полученные результаты позволяют сделать вывод о том, что вторая партия колец подшипников подвергшиеся шлифованию на 36 % состоит из брака. Следовательно, необходимо выявить и устранить причины возникновения погрешностей.

Рассмотрим этот пример с использованием общепринятого подхода к расчету абсолютной и относительной погрешности.

Для партии 1 получаем.

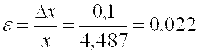На основании общепринятого подхода в качестве абсолютной погрешности берется единица последней значащей цифры. В нашем случае это будет , тогда , то есть погрешность измерений составляет .

Для партии 2 получаем аналогично.

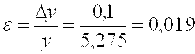, тогда , то есть погрешность измерений составляет .

Таким образом, сравнивая результаты полученных относительных погрешностей можно сделать вывод о том, что общепринятый подход направляет нас на «наложение» постоянной погрешности, равной , а расчет с помощью распределения Стьюдента указывает погрешность свойственную данным показателям.

Список литературы:

1.Богомолов Ю.А. Метрологическая деятельность в современной концепции качества / Ю.А. Богомолов, Д.И. Тверитинов// Измерительная техника. — 2006. — № 5. — с. 8—12. — НБ УлГТУ.

2.Кобзарь А.И. Прикладная математическая статистика. Для инженеров и научных работников. М.: ФИЗМАТЛИТ, 2006 — 816 с.

3.Кочергин А.Н. Основы надежности металлорежущих станков и измерительных приборов (для вузов спец. «тех. машиностр., металлорежущие станки и инструменты»./ А.Н. Кочергин и Л.Д. Ковалев Минск: «Вышэйш. школа», 1974.

4.Смирнов Н.В. Курс теории вероятностей и математической статистики для технических приложений./ Н.В. Смирнов, И.В. Дунин-Барковский. М.: издательство «Наука», 1969 — 512 с.

5.Хан Г. Статистические модели в инженерных задачах. Пер. с анг. Е.Г. Коваленко. Под ред. В.В. Налимова/ Г. Хан, С. Шапиро. М.: «Мир», 1969.

6.Ребро И.В. Прикладная математическая статистика (для технических специальностей) : учеб. пособ. (гриф). Доп. УМО вузов по образованию в области автоматизированного машиностроения (УМО АМ) / И.В. Ребро, В.А. Носенко, Н.Н. Короткова; ВПИ (филиал) ВолгГТУ. олгоград, 2011. — 147 с.