ПРОИЗВЕДЕНИЯ КОНЕЧНОГО ЧИСЛА ВЕКТОРОВ

Бондаренко Раиса Александровна

студент 2 курса, факультет естественных наук и математики, Северо-Восточный государственный университет, г. Магадан

Е-mail: dafnarucia@mail.ru

Магасумов Григорий Супизянович

научный руководитель, доцент кафедры высшей математики, СВГУ, г. Магадан

Цель данной работы — разработать теорию произведений конечного числа векторов по аналогии с произведением четырех, пяти и шести векторов.

В пособии Г.Ф. Лаптева [1] доказано, что:

1.Все произведения четырех векторов выражаются линейно через произведения только двух типов:

1. ,                      2. .

2.Всякое произведение пяти векторов линейно выражается через произведения двух типов:

1. ,                 2..

3.Всякое произведение шести векторов является линейной комбинацией  произведений двух типов:

1.            2.

Рассмотрим произведения конечного числа векторов и предложим два способа исследования.

I способ. Все указанные произведения сводятся к линейной комбинации двух основных произведений, одно из которых является скаляром, а другое — вектором. Сделаем гипотезу — что любое произведение n векторов является линейной комбинацией основных произведений, которые имеют в зависимости от числа n следующий вид.

Если , то основные произведения равны:

              I.           — скаляр,

           II.           — вектор.

Если , то основные произведения имеют вид:

        III.           — скаляр,

       IV.           — вектор.

Будем доказывать для p векторов.

Пусть  (воспользуемся тем, что чётное число p представимо в виде суммы либо двух чётных, либо двух нечетных чисел l и m, а также предположим, что указанная гипотеза верна для этих l и m векторов).

1.  Рассмотрим случай, когда два числа четны

а) Умножим скаляр на скаляр:

 —

это есть произведение вида (I)

б) Умножим скаляр на вектор:

 —

это есть произведение (II)

в) Умножим вектор на вектор скалярно, получим

Вынесем все скаляры за знак скалярного умножения, в скобках получится формула [1, формула (5.7)]

,

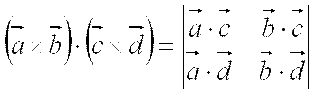а это произведение выражается через основные произведения.

 —

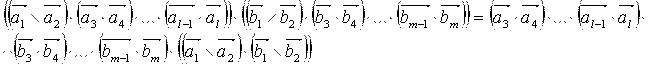произведение типа (I).

г) Умножим вектор на вектор вектор но, тогда имеем

Вынесем все скаляры за знак скалярного умножения, в скобках получится произведение [1, формула (5.14)]

 ,

которое линейно выражается через основные произведения.

 —

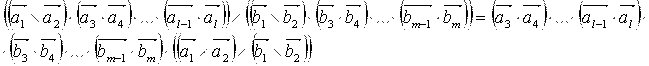произведение типа (II).

2.  Рассмотрим случай,  когда два нечетных числа l и m.

а) Умножим скаляр на скаляр

Вынесем все скаляры за знак скалярного умножения, в скобках получится произведение [1, формула (5.25)]

,

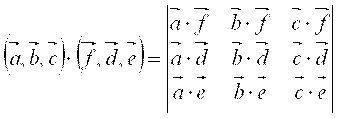которое также выражается через основные произведения.

 —

произведение типа (I).

б) Умножим скаляр на вектор

Вынесем все скаляры за знак скалярного умножения, в скобках получится формула [1, формула (5.16)]

,

представляющая из себя комбинацию основных произведений.

 —

произведение типа (II).

в) Умножим вектор на вектор скалярно

Вынесем за знак скалярного произведения все скаляры, в скобках останется скалярное произведение двух векторов

 —

произведение  типа (I).

г) Умножим вектор на вектор векторно

Вынесем за знак скалярного произведения все скаляры, в скобках останется векторное произведение двух векторов

 —

произведение типа (II).

Пусть +1 (воспользуемся тем, что нечётное число p представимо в виде суммы чётного и нечетного чисел l и m, а также предположим, что указанная гипотеза верна для этих l и m  векторов).

а) умножим скаляр на скаляр

Вынесем за знак скалярного произведения все скаляры, в скобках останется смешанное произведение

 —

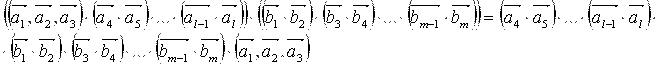произведение типа (III);

б) Умножим скаляр на вектор (скаляр есть произведение чётного числа векторов типа (I), а вектор — нечетного числа векторов типа (IV))

Вынесем за знак скалярного произведения все скаляры, то останется один вектор — это произведения типа (I).

в) Умножим скаляр на вектор (скаляр есть произведение нечётного числа векторов типа (III), а вектор — четного числа векторов типа (II))

Вынесем за знак скалярного произведения все скаляры, то останется произведение, которое можно разложить по формуле [1, формула (5.22)]

,

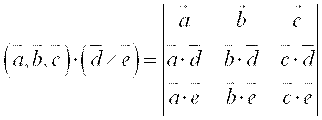то есть получим произведение типа (IV).

г) Умножим вектор на вектор скалярно

Вынесем за знак скалярного произведения все скаляры, тогда останется смешанное произведение, которое является произведением типа (III). 

д) Умножим вектор на вектор векторно

Вынесем за знак скалярного произведения все скаляры,  то останется векторно-векторное произведения, что является типом (IV) 

II способ. Если число k = 2n — чётное, то основными типами произведений являются произведение вида  (вещественное число, являющееся произведением n пар скалярных произведений векторов). Обозначим его через a и назовём произведением I типа для данного параграфа. А также произведение вида  (произведение n — 1 пары скалярных произведений векторов на вектор векторного произведения векторов). Это произведение является вектором, обозначим его через  и назовём произведением II типа.  

Если число k = 2n + 1 — нечётное, то основными типами произведений являются произведение вида  (произведение вещественного числа, являющегося произведением n пар скалярных произведений векторов, на вектор). Это произведение является вектором, обозначим его через  и назовём произведением III типа. А также произведение вида    (произведение n — 1 пары скалярных произведений векторов на смешанное произведение векторов).  Это произведение является числом, обозначим его через b и назовём произведением IV типа для данного параграфа.

Покажем теперь, что если умножать каждый из четырёх типов произведений скалярно или векторно на произвольный вектор , то получится снова произведение одного из указанных типов.

Исследование проведём по возрастанию номера, умножая вначале скалярно, потом векторно. Для I типа: произведение a× есть произведение III типа; произведение a´ смысла не имеет.

Для II типа: произведение × есть произведение IV типа, так как в конце произведения будет смешанное произведение векторов; произведение ´ будет оканчиваться векторно-векторным произведением, которое сводится к простейшим, то есть получится произведение III типа.

Теперь исследуем произведения двух других типов. Для III типа: произведение × есть произведение I типа; произведение ´ есть произведение II типа.

Для IV типа: произведение b× в конце будет содержать произведение четырёх векторов вида . Это произведение сводится к линейной комбинации произведений типа , то есть в целом получим  произведение II типа; произведение b´ смысла не имеет.

В итоге получена полная картина о произведении конечного числа векторов.

Список литературы

1. Лаптев Г.Ф. Элементы векторного исчисления: Учебное пособие для ун-тов. М., Наука, 1975. 330 с.