Статья опубликована в рамках: IV Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 20 сентября 2012 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
СХЕМЫ КВАДРАТИЧНЫХ ФОРМ ЧИСЛОВЫХ ПОЛЕЙ
Онофрийчук Максим Васильевич
студент 3 курса, факультет естественных наук и математики, СВГУ, г. Магадан
E-mail: geassdragoon@mail.ru
Старикова Ольга Александровна
научный руководитель, канд. физ.-мат. наук, доцент СВГУ, г. Магадан
Рассматривается понятие схемы квадратичных форм (quadratic form schemes). Для некоторых числовых полей выявляется строение ассоциированной схемы квадратичных форм.
Введение
Для произвольного поля ![]() группа
группа ![]() вместе с ее определенным отображением на подмножества из
вместе с ее определенным отображением на подмножества из ![]() называется схемой квадратичных форм поля
называется схемой квадратичных форм поля ![]() . Схема квадратичных форм поля полностью определяет его кольцо Витта [2; 4]. Рассматриваются также схемы квадратичных форм с абстрактной группой показателя 2. В § 1 отмечаются некоторые нерешенные вопросы теории схем квадратичных форм, в частности [4, Проблема 1]: всякая ли QF-схема реализуется как QF-схема поля? Известно, что
. Схема квадратичных форм поля полностью определяет его кольцо Витта [2; 4]. Рассматриваются также схемы квадратичных форм с абстрактной группой показателя 2. В § 1 отмечаются некоторые нерешенные вопросы теории схем квадратичных форм, в частности [4, Проблема 1]: всякая ли QF-схема реализуется как QF-схема поля? Известно, что ![]() -схемами поля реализуются выделенные из конечных
-схемами поля реализуются выделенные из конечных ![]() схем локальные и элементарные типы [1; 4].
схем локальные и элементарные типы [1; 4].
Выявляется строение схем квадратичных форм для некоторых числовых полей, именно: в § 2 для полей комплексных и действительных чисел, в § 3 для простых полей Галуа ![]() и
и ![]() , в § 4 для полей
, в § 4 для полей ![]() и
и ![]() адических чисел. В § 5 определяются групповые произведения и групповые расширения
адических чисел. В § 5 определяются групповые произведения и групповые расширения ![]() -схем. Доказана квадратичная эквивалентность поля
-схем. Доказана квадратичная эквивалентность поля ![]() формальных степенных рядов и поля
формальных степенных рядов и поля ![]() адических чисел
адических чисел ![]() .
.
§ 1. Схемы квадратичных форм
В этом параграфе рассматриваются понятия схемы квадратичных форм поля, а также абстрактной ![]() -схемы [4], приводятся некоторые открытые вопросы теории квадратичных форм.
-схемы [4], приводятся некоторые открытые вопросы теории квадратичных форм.
Пусть ![]() — поле и
— поле и ![]() — его мультипликативная группа. Обозначим через
— его мультипликативная группа. Обозначим через ![]() подгруппу обратимых квадратов группы
подгруппу обратимых квадратов группы ![]() , а через
, а через ![]() — факторгруппу
— факторгруппу ![]() . Для
. Для ![]() ,
, ![]() ,
, ![]() множество
множество ![]() есть множество значений бинарной квадратичной формы
есть множество значений бинарной квадратичной формы ![]() . Положим
. Положим ![]() для
для ![]() ,
, ![]() . Схемой квадратичных форм поля
. Схемой квадратичных форм поля ![]() называется структура, состоящая из группы
называется структура, состоящая из группы ![]() , отображения
, отображения ![]() группы
группы ![]() и выделенного элемента
и выделенного элемента ![]() .
.
Всякая ![]() схема
схема ![]() , ассоциированная с полем
, ассоциированная с полем ![]() , обладает следующими свойствами:
, обладает следующими свойствами:
![]()
![]() образует подгруппу группы
образует подгруппу группы ![]()
![]()
![]()
![]()
Замечание [4]. Из ![]() и
и ![]() непосредственно вытекает:
непосредственно вытекает: ![]() .
.
Два поля ![]() и
и ![]() называются квадратично эквивалентными, если ассоциированные с ними
называются квадратично эквивалентными, если ассоциированные с ними ![]() схемы
схемы ![]() и
и ![]() изоморфны, то есть существует групповой изоморфизм
изоморфны, то есть существует групповой изоморфизм ![]() такой, что
такой, что ![]() и
и ![]() .
.
Как отмечается в [4] слишком амбициозно рассчитывать на решение общей задачи классификации полей с точностью до квадратичной эквивалентности. Более достижимой представляется классификация полей с конечной ассоциированной схемой квадратичных форм.
Определяют также и абстрактную ![]() схему
схему ![]() как группу
как группу ![]() экспоненты 2 с выделенным элементом
экспоненты 2 с выделенным элементом ![]() и отображением
и отображением ![]() ,удовлетворяющим условиям
,удовлетворяющим условиям ![]() . Остается открытым следующий вопрос [4]: всякая ли QF-схема реализуется как QF-схема поля?
. Остается открытым следующий вопрос [4]: всякая ли QF-схема реализуется как QF-схема поля?
§ 2. Схемы квадратичных форм полей комплексных и действительных чисел
Построим ![]() схему поля
схему поля ![]() комплексных чисел. Имеем,
комплексных чисел. Имеем, ![]() и, кроме того, подгруппа квадратов
и, кроме того, подгруппа квадратов ![]() мультипликативной группы совпадает с самой группой, то есть
мультипликативной группы совпадает с самой группой, то есть ![]() . Таким образом, факторгруппа
. Таким образом, факторгруппа ![]() состоит только из одного элемента. Получаем,
состоит только из одного элемента. Получаем, ![]() и
и ![]() , так как
, так как ![]() и, тем самым,
и, тем самым, ![]() . Очевидно, множество
. Очевидно, множество ![]() значений бинарной квадратичной формы
значений бинарной квадратичной формы ![]() над
над ![]() есть
есть ![]() . Следовательно, имеет место
. Следовательно, имеет место
Утверждение 1. Схема квадратичных форм поля ![]() комплексных чисел определена условиями:
комплексных чисел определена условиями: ![]() ,
, ![]() ,
, ![]() .
.
Для поля ![]() действительных чисел в силу условия
действительных чисел в силу условия ![]() задача выявления строения схемы квадратичных форм является более интересной. Имеем
задача выявления строения схемы квадратичных форм является более интересной. Имеем ![]() Таким образом факторгруппа
Таким образом факторгруппа ![]() содержит два элемента, представителем класса
содержит два элемента, представителем класса ![]() может служить
может служить ![]() , a число
, a число ![]() выбираем представителем класса
выбираем представителем класса ![]() . Тем самым,
. Тем самым, ![]() и
и ![]() .
.
Множество ![]() есть множество значений бинарной квадратичной формы
есть множество значений бинарной квадратичной формы ![]() . Таким образом,
. Таким образом, ![]() . Аналогично,
. Аналогично, ![]() есть множество значений бинарной квадратичной формы
есть множество значений бинарной квадратичной формы ![]() и
и ![]() .
.
Утверждение 2. Схема квадратичных форм поля ![]() действительных чисел определена условиями: , , ,
действительных чисел определена условиями: , , , ![]() .
.
§ 3. Схемы квадратичных форм конечных полей ![]() и
и ![]()
Пусть ![]() — простое конечное поле, состоящее из трех элементов,
— простое конечное поле, состоящее из трех элементов, ![]() и бинарные операции определены следующим образом:
и бинарные операции определены следующим образом:

Построим схему квадратичных форм поля ![]() . Как показывает таблица умножения,
. Как показывает таблица умножения, ![]() ,
, ![]() . Тогда факторгруппа
. Тогда факторгруппа ![]() состоит из двух элементов
состоит из двух элементов ![]() . Для выделенного элемента
. Для выделенного элемента ![]() получаем
получаем ![]() . Другими словами,
. Другими словами, ![]() не является квадратом в поле
не является квадратом в поле ![]() , так как уравнение
, так как уравнение ![]() не имеет решений.
не имеет решений.
Найдем множества ![]() для каждого элемента
для каждого элемента ![]() группы
группы ![]() . Пусть
. Пусть ![]() , тогда
, тогда ![]() — множество значений квадратичной формы
— множество значений квадратичной формы ![]() . При
. При ![]() ,
, ![]() получаем
получаем ![]() , в случае
, в случае ![]() имеем
имеем ![]() . Таким образом,
. Таким образом, ![]() . Пусть теперь
. Пусть теперь ![]() . Найдем множество
. Найдем множество ![]() значений квадратичной формы
значений квадратичной формы ![]() . При
. При ![]() ,
, ![]() получаем
получаем ![]() , в случае
, в случае ![]() ,
, ![]() имеем
имеем ![]() . Таким образом,
. Таким образом, ![]() . Окончательно, доказано
. Окончательно, доказано
Утверждение 3. Схема квадратичных форм поля ![]() определена условиями:
определена условиями: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Пусть ![]() – простое конечное поле, состоящее из пяти элементов,
– простое конечное поле, состоящее из пяти элементов, ![]() и бинарные операции определены следующим образом:
и бинарные операции определены следующим образом:
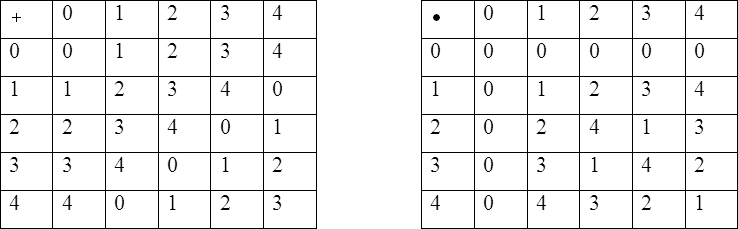
Построим схему квадратичных форм поля ![]() . Как показывает таблица умножения,
. Как показывает таблица умножения, ![]() ,
, ![]() . Тогда факторгруппа
. Тогда факторгруппа ![]() состоит из двух элементов
состоит из двух элементов ![]() . Для выделенного элемента
. Для выделенного элемента ![]() получаем
получаем ![]() .
.
Найдем множества ![]() для каждого элемента
для каждого элемента ![]() группы
группы ![]() . Пусть
. Пусть ![]() , тогда
, тогда ![]() — множество значений квадратичной формы
— множество значений квадратичной формы ![]() . При
. При ![]() ,
, ![]() получаем
получаем ![]() , в случае
, в случае ![]() имеем
имеем ![]() . Таким образом,
. Таким образом, ![]() . Пусть теперь
. Пусть теперь ![]() . Найдем множество
. Найдем множество ![]() значений квадратичной формы
значений квадратичной формы ![]() . При
. При ![]() ,
, ![]() получаем
получаем ![]() , в случае
, в случае ![]() ,
, ![]() имеем
имеем ![]() . Таким образом,
. Таким образом, ![]() .Из данного выше вытекает
.Из данного выше вытекает
Утверждение 4. Схема квадратичных форм поля ![]() определена условиями:
определена условиями: ![]() ,
, ![]() ,
, ![]() .
.
§ 4. Схемы квадратичных форм полей ![]() и
и ![]() адических чисел
адических чисел
Рассмотрим поле ![]() адических чисел
адических чисел ![]() . Каждый элемент поля
. Каждый элемент поля ![]() адических чисел представим в виде:
адических чисел представим в виде:
![]() ,
,
где ![]() и
и ![]()
![]() . Операции сложения и умножения
. Операции сложения и умножения ![]() адических чисел определены, например, в [5]. Несложно показать, что в поле
адических чисел определены, например, в [5]. Несложно показать, что в поле ![]() квадратами являются только те числа, которые имеют вид
квадратами являются только те числа, которые имеют вид ![]() , где
, где ![]() — квадрат в поле
— квадрат в поле ![]() , а остальные коэффициенты
, а остальные коэффициенты ![]() , произвольны. Рассмотрим строение факторгруппы
, произвольны. Рассмотрим строение факторгруппы ![]() . Элементы
. Элементы ![]() попадают в один класс смежности по подгруппе
попадают в один класс смежности по подгруппе ![]() , если
, если ![]() . Так как
. Так как ![]() , то включение
, то включение ![]() равносильно условию
равносильно условию ![]() . Значит, если
. Значит, если ![]() ,
, ![]() , то первый коэффициент произведения
, то первый коэффициент произведения ![]() сравним с
сравним с ![]() по модулю
по модулю ![]() и стоит при степени
и стоит при степени ![]() . Для того, чтобы
. Для того, чтобы ![]() , необходимо и достаточно, чтобы выполнялись два условия:
, необходимо и достаточно, чтобы выполнялись два условия:
1. ![]() — четно, это равносильно тому, что
— четно, это равносильно тому, что ![]() и
и ![]() одновременно четны или одновременно нечетны;
одновременно четны или одновременно нечетны;
2. ![]() — квадратичный вычет по модулю
— квадратичный вычет по модулю ![]() , это равносильно тому, что
, это равносильно тому, что ![]() и
и ![]() одновременно являются квадратами или не квадратами по модулю
одновременно являются квадратами или не квадратами по модулю ![]() .
.
Следовательно, факторгруппа ![]() содержит 4 класса эквивалентности. Их представителями удобно выбрать, соответственно, элементы
содержит 4 класса эквивалентности. Их представителями удобно выбрать, соответственно, элементы ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где:
, где: ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, ![]() . Найдем множества
. Найдем множества ![]() . Согласно определению, а также учитывая
. Согласно определению, а также учитывая ![]() , получаем
, получаем ![]() и
и ![]() . Кроме того,
. Кроме того, ![]() . Таким образом, в силу -
. Таким образом, в силу -![]() получаем
получаем ![]() . Найдем
. Найдем ![]() . Имеем
. Имеем ![]() . Отсюда при
. Отсюда при ![]() получаем
получаем ![]() , в противном случае
, в противном случае ![]() . То есть
. То есть ![]() . Найдем
. Найдем ![]() . Имеем
. Имеем ![]() . Таким образом при любом выборе
. Таким образом при любом выборе ![]() и
и ![]() получаем
получаем ![]() . Найдем
. Найдем ![]() . Аналогично,
. Аналогично, ![]() . Отсюда
. Отсюда ![]() .
.
Утверждение 5. Схема квадратичных форм поля ![]() адических чисел определена условиями
адических чисел определена условиями ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Рассмотрим поле ![]() адических чисел
адических чисел ![]() . Каждый элемент поля
. Каждый элемент поля ![]() адических чисел представим в виде:
адических чисел представим в виде:
![]() ,
,
где ![]() и
и ![]()
![]() . Несложно показать, что в поле
. Несложно показать, что в поле ![]() квадратами являются только те числа, которые имеют вид
квадратами являются только те числа, которые имеют вид ![]() , где
, где ![]() то есть являются квадратами в поле
то есть являются квадратами в поле ![]() , а остальные коэффициенты
, а остальные коэффициенты ![]() , произвольны.
, произвольны.
Следовательно, факторгруппа ![]() содержит 4 класса эквивалентности. Их представителями удобно выбрать, соответственно, элементы
содержит 4 класса эквивалентности. Их представителями удобно выбрать, соответственно, элементы ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где:
, где: ![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, ![]() . В силу
. В силу ![]() получаем
получаем ![]() . Найдем
. Найдем ![]() . Имеем
. Имеем ![]() . Так как уравнение
. Так как уравнение ![]() не имеет не нулевых решений в поле
не имеет не нулевых решений в поле ![]() , то
, то ![]() . В случае
. В случае ![]() или
или ![]() , как и для
, как и для ![]() адических чисел получаем
адических чисел получаем ![]() ,
, ![]() . Имеет место
. Имеет место
Утверждение 6. Схема квадратичных форм поля ![]() адических чисел определена условиями
адических чисел определена условиями ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
§ 5. Операции над ![]() -схемами
-схемами
В этом параграфе определяются групповые произведения и групповые расширения ![]() -схем. Каждая из операций иллюстрируется примерами.
-схем. Каждая из операций иллюстрируется примерами.
Групповые произведения.
Произведением ![]() -схем
-схем ![]() называется группа
называется группа ![]() с выделенным элементом
с выделенным элементом ![]() и отображением
и отображением ![]() , где для элемента
, где для элемента ![]() имеем
имеем ![]() .
.
Построим, например, произведение -![]() схем
схем ![]() и
и ![]() . Согласно определению получаем
. Согласно определению получаем ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Групповые расширения.
Пусть ![]() есть
есть ![]() -схема и
-схема и ![]() — группа второго порядка. Групповое произведение
— группа второго порядка. Групповое произведение ![]() с выделенным элементом
с выделенным элементом ![]() и отображением
и отображением ![]() определенным для
определенным для ![]() следующим образом
следующим образом
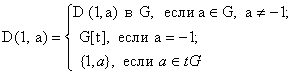
называется групповым расширением ![]() -схемы
-схемы ![]() .
.
Утверждение 7. Поле ![]() формальных степенных рядов квадратично эквивалентно полю
формальных степенных рядов квадратично эквивалентно полю ![]() адических чисел
адических чисел ![]()
Доказательство. Построим схему квадратичных форм поля ![]() формальных степенных рядов над
формальных степенных рядов над ![]() . Согласно [4],
. Согласно [4], ![]() -схема поля
-схема поля ![]() есть групповое расширение
есть групповое расширение ![]() -схемы поля
-схемы поля ![]() . По определению группового расширения получаем
. По определению группового расширения получаем ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
C другой стороны, схема квадратичных форм поля ![]() определена условиями (утверждение 6):
определена условиями (утверждение 6): ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Рассмотрим отображение ![]() , определенное следующим образом:
, определенное следующим образом: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Тогда
. Тогда ![]() — групповой изоморфизм,
— групповой изоморфизм, ![]() и при этом
и при этом ![]() имеем
имеем ![]() . Утверждение доказано.
. Утверждение доказано.
Список литературы:
1.Калужнин Л.А. Введение в алгебру. М.: Наука. 1973.
2.Becher K.J., Hoffmann D.W. Symbol lengths in Milnor ![]() theory. — Homology, Homotopy and Applications. 6 (2004), p. 17—31.
theory. — Homology, Homotopy and Applications. 6 (2004), p. 17—31.
3.Kula M. Fields and quadratic form schemes. — Ann Math.Sil. 1985, 1 (13), p. 7—22.
4.Kula M. Counting Witt rings. — J. Algebra. 1998, 206, no. 2, p. 568—587.
5.Marshall M. The elementary type conjecture in quadratic form theory. — Contemp. Math. 344 (2004), p. 275—293.
дипломов



Оставить комментарий