ОПТИМИЗАЦИОННЫЕ АЛГОРИТМЫ, ПРИМЕНЯЕМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧ НА НАХОЖДЕНИЕ МАКСИМАЛЬНОГО ПОТОКА, ПОТОКА МИНИМАЛЬНОЙ СТОИМОСТИ И ПОТОКА НАИСКОРЕЙШЕГО ПРИБЫТИЯ

Хабибулина Татьяна Васильевна

студентка 4 курса факультет МИТТ ПГУ им. Шолом-Алейхема, г. Биробиджан

Е-mail: Habik_tania@mail.ru

Бабинер Елена Станиславовна

научный руководитель, старший преподаватель кафедры ВМиМОМ ПГУ им. Шолом-Алейхема, г. Биробиджан

Сетевые и графовые модели охватывают довольно большой класс задач, встречающихся при исследовании целого ряда проблем в транспорте, связи и других областях, связанных с действительным или воображаемым движением товаров, информации или людей. Характерной особенностью задач, решаемых с помощью теории графов, является большая размерность поля данных. Поэтому возникает необходимость использования методов оптимизации, которые позволяют экономить вычислительные ресурсы и обеспечивают их гибкость по отношению к изменениям исходных данных.

Одной из таких задач теории графов является задача определения оптимального потока. Поток определяет способ пересылки некоторых объектов из одного пункта в другой. [3].

Для решения задач на определение оптимального потока необходимо освоить оптимизационные алгоритмы, выявить сходства и связь этих алгоритмов.

После изучения литературы, посвященной оптимизационным алгоритмам, были выделены ключевые понятия и определения и выбран единый символический язык. Для более подробного изучения выбраны три алгоритма: поиска максимального потока; поиска потока минимальной стоимости; поиска потока наискорейшего прибытия. Приступив к детальному изучению выбранных алгоритмов, оказалось, что каждый из них использует увеличивающие цепи, поиск которых осуществляется по алгоритму поиска увеличивающей цепи. Поэтому мы остановились и на его детальном рассмотрении.

Следующим шагом было обобщение и структуризация отобранного теоретического материала. Это позволило выявить:

1.  Сходство алгоритмов, а именно, во всех алгоритмах:

·     при задании начальных условий выбирается любой начальный поток из вершины  (источник) в вершину  (сток), то есть любой набор величин , удовлетворяющий соотношениям. Если ни один из начальных потоков из  в  неизвестен, то задается начальный поток, считая, что для всех дуг   [4];

·     определяется состав множеств ,  и  (дуги, в которых поток не может ни увеличиваться, ни уменьшаться (множество ), дуги, в которых поток может увеличиваться (множество ), дуги, в которых поток может уменьшаться (множество ) [4]);

·     применяется алгоритм поиска увеличивающей цепи.

2.  Взаимосвязь алгоритмов:

· при решении задачи на нахождение максимального потока сначала применяется алгоритм поиска увеличивающей цепи, а затем алгоритм поиска максимального потока;

·  решение задачи на нахождение потока минимальной стоимости начинается с применения алгоритма поиска увеличивающей цепи, затем начинает работу алгоритм поиска максимального потока. Выполнение алгоритма заканчивается в том случае, когда найденный поток является в исходном графе максимальным потоком из  в  и имеет при этом минимальную общую стоимость прохождения по соответствующей сети. В противном случае, алгоритм продолжает свою работу (при этом происходит изменение вершинных чисел) до тех пор, пока не будет найден поток минимальной стоимости;

· при решении задачи на нахождение потока наискорейшего прибытия очередность применения алгоритмов такова: алгоритм поиска увеличивающей цепи, алгоритм поиска максимального потока, алгоритм поиска минимальной стоимости, а затем построение потока наискорейшего прибытия.

Таким образом, на лицо преемственность алгоритмов.

После освоения теоретического материала, мы выбрали задачи, при решении которых применяются рассмотренные нами алгоритмы. Это позволило не только на практике понять их работу, но выявить для себя те вопросы, которые в теоретическом изложении остались «за кадром».

Выбранные нами алгоритмы применяются для решения задач на нахождение максимального потока, потока минимальной стоимости и потока наискорейшего прибытия соответственно. Варианты этих задач могут возникнуть в различных практических приложениях.

Задача о максимальном потоке заключается в поиске способа пересылки максимального количества единиц потока из одного пункта в другой при условии отсутствия превышения пропускных способностей дуг исходного графа [5]. Такая задача  возникает, например, когда требуется найти максимально возможный объем некоторой жидкости или газа, который может быть перекачен по сети трубопроводов от источника до пункта потребления или, когда требуется найти максимальный поток транспорта в сети автострад, перевозка товаров по железным дорогам и т. п. [2].

Задача о потоке минимальной стоимости заключается в поиске способа пересылки с минимальными затратами заданного количества единиц потока из одного пункта в другой в графе с заданными на дугах пропускными способностями и стоимостями прохождения одной единицы потока [1]. Такая задача возникает, например, когда некоторый предприниматель имеет возможность выбирать маршруты для перевозки готовых изделий от своего предприятия до склада, с выбором различных маршрутов перевозок связаны те или иные затраты, по каждому маршруту можно пропустить ограниченное количество изделий.

Задача о потоке наискорейшего прибытия заключается в поиске способа пересылки максимально возможного количества единиц потока из одного пункта в другой за определенный период времени в графе с заданными на дугах пропускными способностями. Такая задача  возникает, например, когда за определенный промежуток времени необходимо переправить пассажиров из одного города в другой.

Задача о максимальном потоке

Представитель бюро путешествий должен в один из дней организовать перелет десяти туристов из Чикаго в Стамбул. Имеется семь свободных мест на прямой рейс Чикаго-Стамбул, пять — на рейс Чикаго-Париж и четыре — на рейс Париж-Стамбул. Как должен действовать представитель этого бюро?

Строим сеть, соответствующую условию задачи.

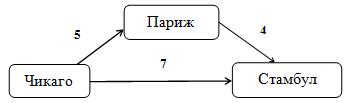
a)

b)

Рисунок 1. Сеть, соответствующая условию задачи

Далее применим к этой сети алгоритм поиска максимального потока. Процедура выполнения алгоритма описана в таблице 1.

Таблица 1.

Процедура выполнения алгоритма поиска максимального потока

Следовательно, через построенную сеть можно пропустить из источника (Чикаго) в сток (Стамбул) 11 единиц потока без превышения пропускных способностей дуг. Поэтому в выбранный день всю группу туристов можно переправить из Чикаго в Стамбул. Четверо из десяти туристов могут осуществить перелет из Чикаго в Стамбул через Париж, а оставшиеся могут отправиться из Чикаго в Стамбул на прямом рейсе. Или семь туристов отправится из Чикаго в Стамбул на прямом рейсе, три туриста — через Париж.

Задача о потоке минимальной стоимости

Представитель бюро путешествий занимается организацией перелета шести туристов, которых необходимо в один из дней отправить самолетом из разных городов по разным маршрутам. Один турист отправляется из Спрингфилда в Рим, двое — из Рима в Париж, трое — из Парижа в Стамбул. В зависимости от маршрута перелет туристов может быть организован через Спрингфилд, Париж, Рим, Стамбул. При чем на рейс Спрингфилд — Париж осталось 2 свободных места, 2 — на рейс Париж — Рим, 2 — на рейс Рим — Стамбул, 1 — на рейс Спрингфилд — Рим, 4 — на рейс Париж — Стамбул и стоимость билетов разная. Каков наилучший с точки зрения затрат вариант перелета группы между указанными пунктами [4]?

Строим сеть, соответствующую условию задачи.

Рисунок 2. Сеть, соответствующая условию задачи

Применим к этой сети алгоритм поиска максимального потока. Результаты выполнения алгоритма сведены в приводимую ниже таблицу.

Таблица 2.

Итерации алгоритма поиска потока минимальной стоимости

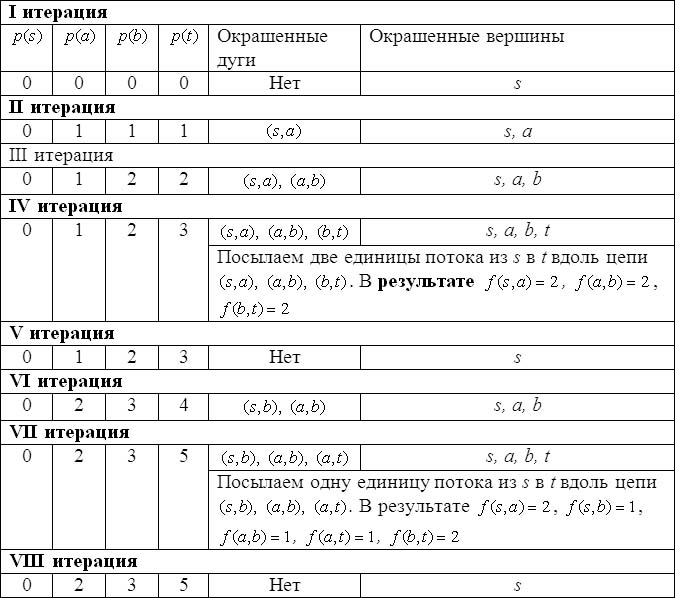
После восьмой итерации оказалось, что ни одна единица потока не может быть передана из  в , так как дуги, ведущие из окрашенных вершин в неокрашенные (а именно дуги  и ), являются насыщенными. Следовательно, полученный поток из трех единиц является максимальным потоком, имеющим минимальную стоимость прохождения по исходному графу (Спрингфилд — Рим — Париж — Стамбул).

Найденный поток удовлетворяет условию задачи. Представитель бюро путешествий в один из дней может организовать перелет шести туристов. Общая стоимость поездки туристов является минимальной. При этом туристы отправятся из разных городов по разным маршрутам. Один турист отправится из Спрингфилда в Рим, двое — из Рима в Париж, трое — из Парижа в Стамбул.

Задача о потоке наискорейшего прибытия

Представитель бюро путешествий из предыдущих примеров ставит перед собой задачу обеспечить доставку наибольшего количества туристов из Спрингфилда в Стамбул через Париж или Рим в течение первого часа, в течение первых двух часов и т. д. вплоть до первых шести часов [4].

Строим сеть, соответствующую условию задачи.

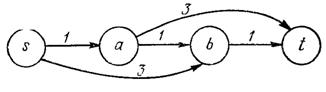
Рисунок 3. Сеть, соответствующая условию задачи

Применим к этой сети алгоритм поиска потока наискорейшего прибытия при .

Применение к этому графу алгоритма поиска потока минимальной стоимости приводит к выявлению всего лишь двух увеличивающих поток цепей, а именно цепи  и цепи  Результат выполнения процедуры нанесения меток описан в таблице 3.

Таблица 3.

Выполнения процедуры нанесения меток

Полученное множество меток соответствует потоку наискорейшего прибытия в сети, соответствующей условию задачи за период в шесть интервалов времени.

Оптимизационные алгоритмы освоены и применены для решения задач на потоках, выявлены сходства и связь этих алгоритмов. Подводя  итоги, можно отметить следующее:

· применение аппарата теории графов к решению различных классов задач на первый взгляд выглядит довольно громоздким, но его простота, наглядность и рациональность определяют широту использования в различных сферах производства;

· легкость восприятия дает возможность использовать данный материал не только в высших учебных заведениях, но и внедрять его в программу факультативных занятий для старшеклассников, что в свою очередь способствует созданию четкого представления о тех задачах, с которыми предстоит сталкиваться в выбранной профессии и созданию базы для формирования ключевых профессиональных компетенций.

Список литературы:

1. Белов В.В., Воробьев Е.М., Шаталов В.Е. Теория графов. М.: Высшая школа, 1976. — 392 с.

2. Гончаров Г.А., Мочалин А.А. Элементы дискретной математики: Учебное пособие. М.: ФОРУМ: ИНФРА-М, 2003. — 128 с.

3. Логинов Б.М. Введение в дискретную математику. М.: Калуга, 1998. — 423 с.

4. Майника Э. Алгоритмы оптимизации на сетях. М.: Мир, 1981. — 323 с.

5. Свами М., Тхуласираман К. Графы, сети и алгоритмы. М.: Мир, 1984. 455 с.