ОБОСНОВАНИЕ ВИДА ПРОГРАММНОЙ ТРАЕКТОРИИ ДВИЖЕНИЯ ОСЕСИММЕТРИЧНОЙ ДЕТАЛИ В ПРОЦЕССЕ АДАПТАЦИИ

Балашов Даниил Андреевич

Маштаков Максим Валерьевич

студенты 4 курса, кафедра Приборостроение Федерального государственного бюджетного общеобразовательного учреждения высшего профессионального образования «Ковровская государственная технологическая академия имени В. А. Дегтярева»,  г. Ковров

E-mail: kremlnasvyazi@mail.ru

Кабаева Ольга Николаевна

научный руководитель,канд. техн. наук, доцент кафедры Приборостроение Федерального государственного бюджетного общеобразовательного учреждения высшего профессионального образования «Ковровская государственная технологическая академия имени В. А. Дегтярева»,  г. Ковров

Исходя из необходимых условий автоматизированного совмещения сопрягаемых поверхностей [3, с. 53], [4, с. 26] программная траектория совмещения определяется оператором линейного преобразования начальных

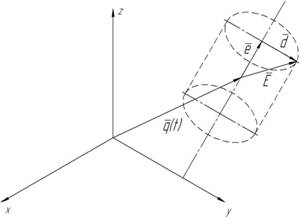
Рис. 1. Пространственная ориентация МПБ в прямоугольной системе координат

координат модуля базирующей поверхности (МПБ)[1, с. 30] в конечные (согласованные) значения. В общем случае соединяемая деталь (и МПБ)  имеет 6 степеней подвижности (3 угловых и 3 линейных) и программная траектория совмещения является пространственной кривой. Для описания пространственного положения и ориентации МПБ соединяемой детали целесообразно использовать классификацию характеристик движения совмещения деталей [3, с. 57]. В соответствии с ней все модули соединения (МС) (базовые) можно разделить на 2 группы: МС, имеющие конечное  число плоскостей симметрии (n=0, 1,…m) и МС, с бесконечным числом плоскостей симметрии (n=). К первой группе относятся: соединения по плоскостям или цилиндрическим поверхностям (профильные, шпоночные, ласточкин хвост, шлицевые, зубчатых колес и их комбинации).  При совмещении для них необходимо обеспечить ориентацию по 2 линейным и 3 угловым координатам, число согласованных положений для модулей базирующих поверхностей при этом конечно (k=1…m) [3, с. 62]. Пространственное положение и ориентация этих МПБ  в прямоугольной системе координат может быть описана с помощью следующих векторов:  - вектор,  определяющий положение центра масс детали (или ее геометрического центра),  - единичный вектор, определяющий ориентацию оси совмещения МПБ, - вектор, определяющий положение характерной точки (поверхности) МПБ относительно оси совмещения (вектора) (рис. 1). Поскольку параметры векторов  и  в системе координат, связанной с деталью неизменны, ориентация детали в пространстве может задана вектором

Кинематика движения детали в процессе адаптации иллюстрируется в общем случае МПБ рисунком 2. Относительная адаптация соответствует изменению вектора  из начального  в конечное  положение. При этом изменяется как направление, так и модуль этого вектора. Угловая адаптация состоит в преобразовании вектора  в положение  . Модуль вектора  в этом преобразовании не изменяется. При позиционном методе управления движением детали промежуточные значения векторов  и  не контролируются, поэтому программная траектория совмещения может иметь произвольный вид.  Перемещение по такой траектории характеризуется вектором . 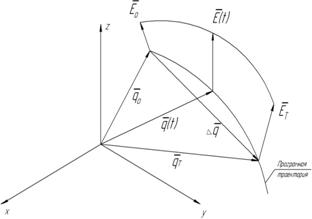Вектор   при этом может рассматриваться как, скользящий вектор, участвующий в винтовом движении вдоль вектора  (рис. 3): линейное перемещение  обозначим  и угловое перемещение .

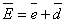
Суммарное перемещение вектора  по прямой траектории характеризуется винтом, где - мнимая единица,  [2, с. 61]. Поскольку вектор  определяет ориентацию и положение МПБ соединяемой детали, оператор линейного преобразования этого вектора может быть найден в виде матрицы с дуальными элементами, описывающей поступательное и угловое перемещение вектора. Представим винт Q в виде проекций на оси координат x, y, z. Каждая из проекций будет описывать дуальные (винтовые) перемещения вектора  вдоль соответствующей оси координат. Введем обозначение этих проекций:

;

;

;

;

 - углы поворота вектора  вокруг осей ox, oy, oz;

 - поступательные перемещения вектора  вдоль осей ox, oy, oz.

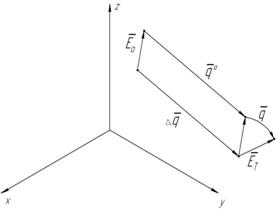
Винтовые  перемещения вектора из положения  в положение   соответственно можно представить как три винтовых перемещения вдоль координатных осей.

Каждое из этих  перемещений описывается матрицей с дуальными элементами:

по оси x - ;                         (1)

по оси y - ;                         (2)

по оси z - 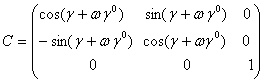.                          (3)

Начальные координаты вектора =(Е_хо, Е_уо,Е_zо)^Т ; . Конечные координаты вектора , определяющие согласованные положение и ориентацию детали в момент окончания этапа адаптации -  . С учетом  дуальных преобразований, описываемых матрицами (1), (2), (3) можно записать

Матрица с дуальным элементом , совпадающая с винтом  преобразования вектора , и является оператором линейного преобразования этого вектора по программной траектории совмещения. Найдем ее выражение через дуальные углы :

;                                 (4)                

где ;

;

;

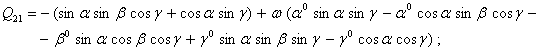
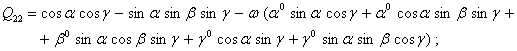
Эта матрица осуществляет аффинные преобразования вектора  и является дуальным аффинором [2, с. 63]. Дуальные углы  определяют линейное и угловое рассогласование МПБ соединяемых деталей. Программная траектория движения детали при позиционном управлении должна удовлетворять условию:

,

где Т – время перемещения; - допустимая погрешность;  - вектора, определяющие начальное и конечное положение центра масс детали.

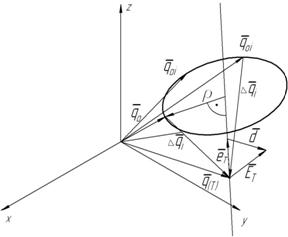
 Таким образом, перемещение из начальной позиции в конечную по программной траектории должно обеспечить наибольшую производительность при ограничении скорости и ускорений перемещения.  В соответствии с этими ограничениями программная траектория является прямой линией, совпадающей с вектором  (рис. 3). Определим геометрическое место программных траекторий совмещения при наличии рассеяния начального положения соединяемой детали. Осью, относительно которой с равной вероятностью могут располагаться начальные положения соединяемой детали, является направление вектора , задающего положение оси совмещения базовой детали (рис. 4).

Радиус рассеяния  равен расстоянию от конца вектора   до оси совмещения. Окружность рассеяния определяет границу возможных  начальных положений соединяемой детали. Поскольку положение  постоянно, а вектор  может принимать множество значений  , ограниченное годографом - окружностью рассеяния радиусом , множество программных траекторий совмещения  образует линейчатую поверхность  - конус (рис.3).

С учетом допустимой погрешности  положения  эта поверхность принимает вид усеченного конуса с окружностью радиуса  у вершины. Геометрическим местом программных траекторий в более общем случае является объем внутри указанной конической поверхности. Матрицы преобразования дуальных координат для любой из программных траекторий имеют вид (4).  Различными для них будут только значения дуальных углов .

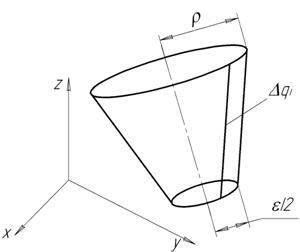
 Рис. 5. Множество программных траекторий позиционного совмещения

Таким образом, на основании кинематических преобразований дуальных координат получено геометрическое место программных траекторий позиционного совмещения для деталей произвольного вида.

Список литературы:

1.Базров В. М. Модульный принцип в построении сборочного производства // Вестник машиностроения, 1997. № 1, с. 30‑33.

2.Диментберг Ф. М. Теория винтов и ее приложения // Главная редакция физико-математической литературы издательства «Наука», М.: 1978. – 328 с.

3.Кабаева О. Н. Разработка способа и средств пассивной адаптации деталей различных видов соединений при автоматизированной сборке на основе метода позиционирования / дисс. на соиск. уч. ст. д. техн. н. – Ковров: 2006 г.

4.Симаков А. Л. Обоснование методов и средств адаптации соединяемых деталей на базе принципов автоматического управления и выявленных взаимосвязей при автоматизированной сборке / дисс. на соиск. уч. ст. д. техн. н. – Ковров: 2002 г.