ОСОБЕННОСТИ  СОСТАВЛЕНИЯ  ДИФФЕРЕНЦИАЛЬНЫХ  УРАВНЕНИЙ  ПРИ  РЕШЕНИИ  ИНЖЕНЕРНО-ТЕХНИЧЕСКИХ  ЗАДАЧ

Орлова  Виктория  Владимировна

студент  5  курса,  физико-математический  факультет  ФГБОУ  ВПО  «ЧГПУ  им.  И.Я.  Яковлева»,  РФ,  г.  Чебоксары

E -mail:  122992@mail.ru

Пономарева  Татьяна  Тажутиновна

научный  руководитель  ,  канд.  физ.-мат.  наук,  доцент  кафедры  математического  анализа  ФГБОУ  ВПО  «ЧГПУ  им.  И.Я.  Яковлева»,  РФ,  г.  Чебоксары

В  курсах  по  решению  практических  инженерно-технических  задач  особенностям  составления  дифференциальных  уравнений  уделяется  недостаточное  внимание,  особенно  в  педагогических  институтах.  Исходя  из  вышесказанного,  целью  данной  работы  стало  желание  оказать  студентам  помощь  в  овладении  навыками  составления  и  решения  дифференциальных  уравнений  по  условиям  инженерно-технических  задач,  возникающих  в  процессе  обучения  или  научной  деятельности.

Работа  состоит  из  двух  разделов.  В  первом  разделе  помещены  задачи,  которые  относятся  к  задачам,  решаемым  дифференциальными  уравнениями  первого  порядка  по  разным  направлениям  курса  физики  инженерно-технического  характера.  По  содержанию  задачи  охватывают  ряд  научно-технических  дисциплин  и  раскрывают  связь  дифференциальных  уравнений  со  смежными  научными  дисциплинами.  Во  втором  разделе  работы  рассмотрены  задачи,  решаемые  с  помощью  дифференциальных  уравнений  второго  порядка,  по  аналогии  с  первым  разделом.

Раздел  1.

Задача  1  (механика).  В  какое  время  вода,  заполняющая  полусферическую  чашу  диаметра  2  м,  вытечет  из  нее  через  круглое  отверстие  радиуса  0,1  м,  вырезанное  на  дне  чаши?

Решение:   Если  бы  не  происходило  потери  энергии,  то  скорость,  с  которою  вода  вытекала  из  отверстия,  расположенного  на  расстоянии    по  вертикали  ниже  свободной  поверхности,  равнялась  бы  скорости  свободно  падающего  тела,  прошедшего  путь  ,  т.  е.

.

В  силу  трения  и  условий,  связанных  с  формою  сосуда,  эта  скорость  в  среднем  равна

где  в  обычных  условиях  можно  принять  приблизительно 

Рисунок  1.  Полусферическая  чаша

Итак,  пусть    есть  высота  воды  в  момент  времени  ,  и 

·     радиус  круга,  образуемого  ее  свободной  поверхностью.  Масса  воды,  вытекающая  из  сосуда  в  промежуток  времени  ,  образует  цилиндр,  высота  которого  есть  ,  а  основание  —  круг  радиуса  0,1  м.  Объем  этой  массы  есть,  следовательно,

Вследствие  этого  истечения  в  сосуде  освобождается  от  воды  слой,  приближенно  имеющий  форму  цилиндра,  высота  которого  есть  —  ,  а  радиус  основания  ,  и,  следовательно,  объем 

Таким  образом  мы  получаем: 

Разделяя  переменные,  мы  находим:

Ответ:  .

Задача  2  (сопротивление  материалов  и  строительная  механика).  Стальная  проволока  длиной    м  защемлена  в  одном  из  концов  и  под  действием  своего  веса  находится  в  положении  равновесия.  Объемный  вес  стали  ,  .  Определить  удлинение  проволоки.

Решение:  Величина  натяжения    меняется  в  зависимости  от  места  сечения.  Это  натяжение  равно  весу  нижерасположенной  части  проволоки.  Поэтому  различные  элементы  проволоки  растягиваются  различно.  В  точке,  на  расстоянии    от  закрепления,  элемент    испытывает  натяжение  ,  определяемое  из  пропорции 

где:  —  вес  всей  проволоки.

Удлинение  проволоки    (в  метрах)  под  влиянием  растягивающей  силы    (в  кГ)  будет:

,

где:    —  коэффициент  удлинения, 

  —  площадь  поперечного  сечения,  в  .

Для  растяжения  элемента    имеем: 

или

.

Но,  с  другой  стороны,  (в  кГ),  если    измеряем  в  см.  Подставляя  последнее  выражение  для  P  в  последнее  уравнение,  получим  дифференциальное  уравнение  процесса:

.

Интегрируя,  получим  полное  удлинение:

,

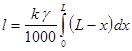Или

.

Ответ: 

Раздел  2.

Задача  3  (механика).  Маятник,  состоящий  из  небольшого  тела  массы  ,  привешенного  к  нити  длины  ,  качается  в  среде,  сопротивление  которой  пропорционально  скорости.  Найти  период  колебания.

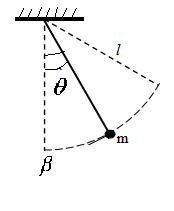
Рисунок  2.  Математический  маятник

Решение.   Момент  веса  маятника  относительно  точки  привеса  есть  ;  знак  отрицателен  потому,  что  при  положительном  угле    момент  стремиться  уменьшить  этот  угол.  Скорость  точки    есть 

.

Следовательно,  величина  сопротивления  среды  есть

.

Момент  же  этого  сопротивления  есть

;

он  отрицателен  при  положительных  значениях  .  Вследствие  чего  мы  и  ставим  знак  «-»  перед  его  выражением.

Наконец,  момент  инерции  маятника  есть  .  Поэтому  общее  уравнение 

в  нашем  случае  принимает  вид:

.

Заменяя    через  ,  мы  получаем

.

Решение  этого  уравнения  имеет  вид

,

и,  следовательно,  период  колебаний  равен 

.

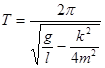Ответ: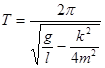 

ЗАКЛЮЧЕНИЕ

Данная  работа  поможет  повысить  уровень  математической  подготовки  студентов  на  основе  более  углубленного  изучения  раздела  математического  анализа  —  дифференциальные  уравнения  —  с  учетом  общеинженерных  и  специальных  дисциплин.  Рассмотренные  особенности  составления  дифференциальных  задач  при  решении  инженерно-технических  задач,  будут  полезны  для  студентов  первых  курсов  в  изучении  физики  и  др.  дисциплин,  а  программы,  составленные  на  их  основе,  могут  упростить  выполнение  любых  лабораторных  работ.

Статья  предназначена  для  студентов  стационарных  и  заочных  педагогических  институтов  и  лиц,  самостоятельно  изучающих  курс  физики.  Статья  может  быть  полезна  также  преподавателям  старших  классов  средней  школы  при  проведении  занятий  в  физико-математических  кружках  и  студентам  высших  технических  учебных  заведений.

Список  литературы:

1.Амелькин  В.В.  Математические  модели  и  дифференциальные  уравнения.  /  В.В.  Амелькин,  А.П.  Садовский.  Минск:  Вышэйшая  школа,  1982.  —  272  с.

2.Андронов  А.А.  Теория  колебаний.  /  А.А.  Андронов,  А.А.  Витт,  С.Э.  Хайкин  М.:  Физматгиз,  1959.  —  916  с.

3.Пономарев  К.К.  Составление  дифференциальных  уравнений.  /  К.К.  Пономарев  Минск  :  Наука  и  техника,  1979.  —  744  с.

4.Филипс  Г.  Дифференциальные  уравнения.  /  Г.  Филипс  М.:  Государственное  технико-теоретическое  издательство,  1932.  —  80  с.