МЕТОД ЛАНЦОША ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ СОСТОЯНИЙ

Амбарцумов Михаил Георгиевич

студент 3 курса, кафедры технологии наноматериалов, СКФУ, г. Ставрополь

Винокурский Дмитрий Леонидович

научный руководитель, канд. физ.-мат. наук, доцент СКФУ, г. Ставрополь

Энергия, плотность состояний, силы любой сложной молекулярной системы (кластер, твердое тело, большие молекулы) определяются через гамильтониан Н [2]. Определим функцию Грина молекулярной ситемы:

                                                     (1)

Гамильтониан системы выразим через собственные значения:

                                                                (2)

Преобразуем функцию Грина:

                                         (3)

Введем новую функцию  называемую резольвентой.

Пусть , тогда мнимая часть резольвенты может быть определена следующим образом:

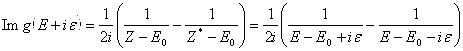             (4)

Таким образом

                                      (5)

Рисунок 1. График резольвенты в зависимости от энергии кристалла

Рассмотрим некоторые свойства резольвенты.

                                             (6)

Аналогично находим, что

                                 (7)

Рекуррентный метод определения плотности состояний

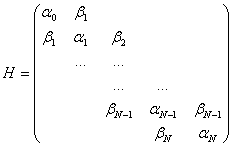
Пусть с помощью ортогонального преобразования U удалось преобразовать гамильтониан системы к трёхдиагональному виду:

                                       (8)

Тогда функция Грина трехдиагонального гамильтониана H_TD может быть получена с помощью преобразования:

                                                  (9)

Пусть квантовая система может находиться в N состояниях, заданных с помощью векторов . Данные векторы ортогональны между собой, то есть , где  — символ Кронекера [3].

В этом случае можно представить гамильтониан в виде [3]:

                              (10)

Покажем как можно построить эту систему собственных векторов. Используя метод Ланцоша. Определим произведение гамильтониана на вектор.

                           (11)

Далее, используя стандартный алгоритм метода Ланцоша построим ортогональную систему собственных векторов .

С помощью найденных ортогональных преобразований можно получить разложение функции Грина в цепную дробь.

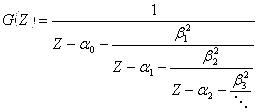                         (12)

Построим оценку значений функции Грина. Если все значения гамильтониана равны между собой, то получим следующую цепную дробь, которая будет верхней границей нашей функции Грина:

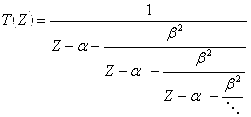                           (13)

Эту функцию можно переписать в виде:

                                    (14)

Решая последнее уравнение, получим следующую формулу для верхней границы функции Грина:

                                  (15)

Аналитические примеры

Для иллюстрации метода воспользуемся простейшей моделью описания молекулярных систем — моделью Хюккеля. Построим гамильтониан молекулы бензола в приближении p — электронов.

Рисунок 2. Молекула бензола

Гамильтониан p — электронной системы в методе Хюккеля запишется в виде:

                                          (16)

Используя, описанный выше, метод Ланцоша приведем гамильтониан к трехдиагональному виду.

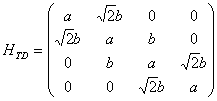                                  (17)

Функция Грина данной задачи принимает вид:

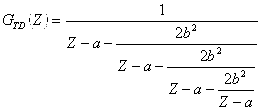                         (18)

Определим плотность состояний для p — электронов молекулы бензола.

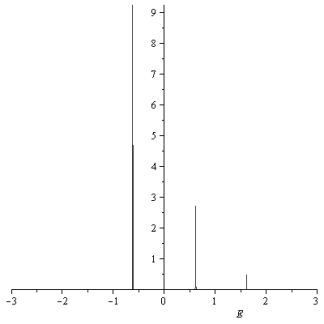
Рисунок 3. Плотность состояний p — электронов бензола

Рассмотрим решетку полубесконечную решетку, состоящую из атомов, имеющих одну s-орбиталь (решетку Бете). Ограничимся учетом влияния ближайших соседей. В этом случае имеются следующие не нулевые значения гамильтониана

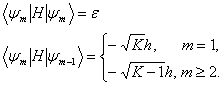                       (19)

Используя описанный выше алгоритм Ланцоша, получим следующую функцию Грина для данной задачи:

                      (20)

Для иллюстрации построим график плотности состояний в решетке Бете.

Рисунок 4. Плотность состояний для решетки Бете.

Определение плотности состояния кристалла с помощью функции Грина

В теории функционала электронной плотности полная энергия кристалла определяется следующим выражением:

.   (21)

Здесь первое слагаемое представляет собой кинетическую энергию электронов в кристалле;  — заселенность орбитали ν, σ — спиновая переменная (α — спин вверх, β — спин вниз);  — волновая функция. Второе слагаемое в выражении (21) — энергия элетрон-ядерного взаимодействия. В этом выражении  — оператор плотности элетрического заряда. Третье слагаемое в формуле (21) представляет собой энергию элетрон-элетронного взаимодействия. Последнее слагаемое в данной формуле описывает обменно-корелляционное взаимодействие.

Иначе формулу (21) можно представить в виде:

,                    (22)

где  — зонная энергия,

 — потенциал Хартри,

 — потенциал обменно-корреляционного взаимодействия,

 — операция вычисления следа матрицы.

Используя развитый выше формализм функций Грина можно определить матрицу плотности:

.                      (23)

Здесь  — функция Ферми и ε — бесконечно малая положительная величина. Как видно из формулы (22) плотность состояний в кристалле полностью определяется плотностью электрического заряда, которая может быть определена из функционала (21) или (22). Также через функции Грина может быть определена и заселенность орбиталей по Милликену:

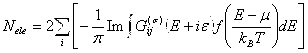                         (24)

Выше указанные алгоритмы позволяют однозначно определить плотность состояний сложных молекулярных систем, а, следовательно, энергетический спектр этих систем. Преимуществом данного метода перед традиционными [1, 2] является его простота при моделировании на компьютере.

Список литературы:

1. Займан Дж. Принципы теории твердого тела. М.: Мир, 1974, — 500 с.
2. Киттель Ч. Квантовая теория твердых тел. М.: Наука, 1967. — 600 с.
3. Taisuke Ozaki. Note on recursion methods. Ibaraki. Japan, 2003