Исследование поверхностного натяжения расплавов

Цыбиктаров Баяр Борисович

студент 1 курса физико-технического факультета Бурятского государственного университета, г. Улан-Удэ

Баинов Борис Сономович

ученик 10 физико-математического класса гимназии № 33, г. Улан-Удэ

Е-mail: abain76@list.ru

Дамбуева Альбина Борисовна

научный руководитель, канд. физ. мат. наук, доцент БГУ, г. Улан-Удэ

Профессором Сандитовым Д.С. была предложена модель возбужденных атомов, основанная на предположении о существовании в аморфной конденсированной среде небольшого числа возбужденных кинетических единиц — атомов, смещенных на критическое расстояние, соответствующее максимуму силы межатомного притяжения. 

В нашей работе, используя микроскопическую трактовку энергии активации, полученную в рамках модели возбужденных атомов, дана альтернативная оценка энергии активации  и получена ее связь с поверхностным натяжением .

Определим основные параметры модели, необходимые для дальнейшего изложения. Образование и исчезновение возбужденных кинетических единиц происходят в результате тепловых флуктуаций и под действием внешних воздействий. При предельном отклонении атома нарушается линейная зависимость межатомных сил от смещения и наблюдается явление ангармонизма.

Для перехода атома в возбужденное состояние требуется активационный объем v_h, который определяется изменением степени локального беспорядка структуры. Вероятность критического смещения атома выражается соотношением

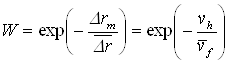,                              (1)

где  — среднее смещение атома, для которого можно записать уравнение Клаузиуса в трактовке, применимой к жидкостям и стеклам:

,

pd² — площадь сечения, приходящаяся на атом, n — концентрация атомов, смещенных из временного равновесного положения (из «центра ячейки»), равная обратной величине среднего активационного объема:

.

Активационный объем v_h, необходимый для критического смещения атома, определяется выражением

.                                               (2)

Суммарный активационный объем, равный произведению активационного объема  на среднее число возбужденных атомов  , называется флуктуационным объемом системы.

Для определения энергии активации  рассмотрим уравнение состояния, представляющее собой условие баланса, по которыму внешнее давление P совместно с внутренним молекулярным давлением P_i, обусловленным силами межатомного притяжения, уравновешивают тепловое давление P_t=nkT, действующее на поверхность системы изнутри:

P+P_i=nkT.

Внутреннее давление определяется потенциальным полем, созданным ближайшим окружением частицы и быстро убывает с величиной ее смещения. Поэтому в первом приближении P_i считаем постоянным и равным его максимуму P_i@P_m@const, соответствующему критическому смещению [2, 4].

Поэтому для концентрации смещенных атомов можно записать следующее соотношение:

,

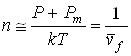Подставляя это соотношение в формулу (1) получим уравнение

,                                           (3)

Тогда для энергии активации e_h, равной  работе смещения атома на критическое расстояние, запишем:

.                                                  (4)

Таким образом, основные параметры модели имеют следующую микроскопическую интерпретацию:  — это минимальный объем, необходимый для образования возбужденного атома;  — это работа по перемещению атома на критическое расстояние.

Далее рассмотрим связь поверхностного натяжения с энергией активации. Коэффициент поверхностного натяжения жидкости s  можно рассматривать как работу, необходимую для увеличения ее поверхности на единицу площади путем растяжения, которое сопровождается критическими удлинениями связей между атомами Dr_m [4]. При отрыве  друг от друга двух единичных площадок по 1, связанных между собой силами межатомного притяжения, обнажается поверхность площадью в 2, т. е. поверхность жидкости увеличивается на величину 2. Для этого, по определению s, необходимо совершить работу

,                                         (5)

где P_i(x)  — внутреннее молекулярное давление, равное силе притяжения между атомами, отнесенной к единице площади, x — расстояние между площадками. Поскольку сила межатомного притяжения действует на малых масштабах, как отмечалось выше, величину P_i можно заменить ее максимальным значением P_m, а расстояние dx — предельным растяжением связи Dr_m [1, 3].

При переходе от единичных площадок к предельной деформации связи между соседними атомами в равенстве (5) вместо s  следует брать атомарное поверхностное натяжение s_А=spd²:

.                        (6)

Выразив площадь сечения атома pd² через атомный объем v_A, приходим к выводу о том, что энергию активации критического смещения атома можно рассчитать по данным о поверхностном натяжении и атомном объеме

e_h=2sv_А^2/3 N_А^1/3,                                      (7)

где N_А — число Авогадро. Атомный объем нами рассчитан по данным о плотности r и средней массе атома А:

v_A=A/r, A=Sv_i M_i /Sv_i n_i,

где v_i и M_i  — соответственно, молярная доля и масса i-го окисла,  n_i — число атомов в i-м окисле.

Как видно из таблицы 1, у ряда аморфных полимеров (ПС, ПБ) и силикатных стекол результаты расчета e_h по формуле (7) находятся в хорошем согласии с данными для e_h, полученными традиционным способом по соотношению:

e_h=RT_gln(1/f_g),                                             (8)

В рамках модели возбужденных атомов с помощью формул (7) и (8) можно оценить поверхностное натяжение стеклообразных систем

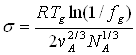.                                       (9)

Получено вполне удовлетворительное согласие этого выражения  с опытными данными (табл. 1).

В таблице 1 обозначение стекол дано по каталогу фирмы “Schott”: F2 — флинт, SF64 — тяжелый флинт, 8209 — телевизионная трубка, 8330 — стекло для спаев с коваром, 8558 — стекло «Дуран-50». Для этих стекол f_g определена по уравнению (8), а для остальных стекол — по уравнению Вильямса-Ландела-Ферри.

Таблица 1

Поверхностное натяжение s и параметры модели флуктуационного объема аморфных полимеров (ПС и ПБ) и неорганических стекол

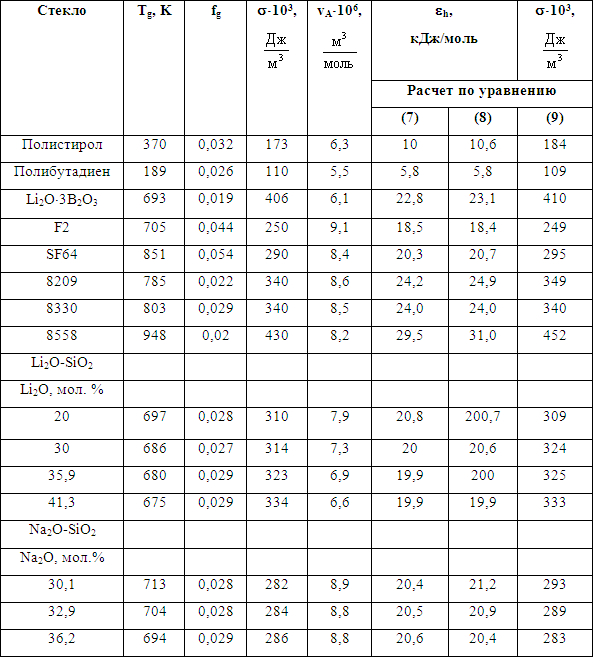
Таким образом, согласие результатов расчета e_h и s с экспериментальными данными подтверждает представление о том, что образование возбужденного атома обусловлено предельной деформацией межатомной или межмолекулярной связи, соответствующей максимуму силы притяжения между атомами (молекулами).

Список литературы:

1.Бартенев Г.М. Структура и релаксационные свойства эластомеров. М.: Химия, 1979. — 288 с.

2.Сандитов Д.С., Бартенев Г.М. Физические свойства неупорядоченных структур. Новосибирск: Наука, 1982. — 259 с.

3.Ферри Дж. Вязкоупругие свойства полимеров. М.: ИЛ, 1963. — 535 с.

4.Френкель Я.И. Кинетическая теория жидкостей. М. — Л.: Изд. АН СССР, 1945. — 424 с.