ИЗУЧЕНИЕ  ЭЛЕМЕНТОВ  ТЕОРИИ  МНОЖЕСТВ  НА  ПРИМЕРЕ  ИХ  ПРИЛОЖЕНИЯ  В  КОМПЬЮТЕРНОМ  МОДЕЛИРОВАНИИ

Сенник  Оксана  Николаевна

магистрант,  кафедра  математического  анализа  КемГУ,  РФ,  г.  Кемерово

E-mail:  AKSUNYA.1990@YANDEX.ru

Даурцева  Наталья  Александровна

научный  руководитель,  канд.  физ.-мат.  наук,  доцент  КемГУ,  РФ,  г.  Кемерово

Теоретико-множественные  понятия  встречаются  практически  во  всех  разделах  современной  математики  и  составляют  ее  фундамент.  Язык  теории  множеств  является  средством,  с  помощью  которого  может  быть  построен  школьный  курс  математики.  Теоретико-множественный  подход  способствует  развитию  общей  культуры  учащихся,  помогает  видеть  связи  между  явлениями.  Таким  образом,  теоретико-множественный  подход  при  изучении  школьного  курса  математики,  способствует  выявлению  связей  между  различными  разделами  математики,  помогает  развитию  математической  культуры  учащихся.

Зачастую,  предлагаемый  материал  по  элементам  теории  множеств,  не  воспринимается  обучающимися  должным  образом.  Это  связано  в  первую  очередь  с  тем,  что  ученики  не  представляют  практической  значимости  данной  теории.  Материал  для  них  не  имеет  смыла  и  занятия  становятся  скучными.  Чтобы  этого  избежать,  необходимо  подобрать  специальную  систему  упражнений,  позволяющую  увидеть  применение  основных  операций  теории  множеств  в  окружающем  мире.

Начать  изучение  элементов  теории  множеств  следует  с  введения  основных  понятий.  Множество  одно  из  основных  понятий  современной  математики.  Это  понятие  не  сводится  к  другим  понятиям  и  не  определяется.  Вместо  определения  привести  несколько  примеров  множеств:

·     множество  натуральных  чисел

·     множество  точек  на  плоскости

·     множества  типа:  куб,  шар,  параллелепипед,  цилиндр  и  т.  д.

Когда  в  математике  говорят  о  множестве,  то  подразумевают  совокупность  предметов  (объектов),  объединенных  в  одно  целое  по  некоторому  признаку.

Предметы  (объекты),  составляющие  множество,  называют  его  элементами.  Множества  принято  обозначать  заглавными  латинскими  буквами  А,  В,  С….

Рассмотрим  два  множества  А  и  В.  Если  каждый  элемент  множества  А  является  элементом  множества  В,  то  говорят,  что  А  —  подмножество  множества  В.  Записывается  это  так:  .  Множества  удобно  изображать  окружностями  или  областями.  (Рис.  1).

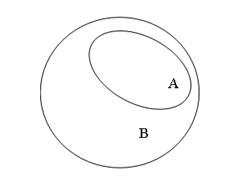
Рисунок  1.  Подмножество  А  множества  В

Примеры  множеств  и  их  подмножеств:

·     Множество  действительных  чисел  ,  множество  натуральных  чисел  ,  ;

·     Множество  букв  русского  алфавита  обозначим  за  А,  множество  гласных  букв  обозначим  за  В,  .

После  введения  основных  понятий  следует  перейти  к  изучению  операций  над  множествами.  Три  основные  операции:

1.  Пересечение  или  произведение  множеств;

2.  Объединение  множеств;

3.  Разность  множеств.

Пересечением  (произведением)  множеств  А  и  В  называется  множество,  состоящее  из  всех  элементов,  принадлежащих  одновременно  и  множеству  А,  и  множеству  В.  Обозначают  пересечение  множеств  .  .  (Рис.  2).

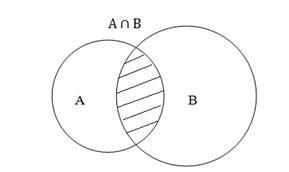
Рисунок  2.  Пересечение  (произведение  множеств)

Объединением  двух  множеств  А  и  В  называется  множество,  состоящее  из  всех  элементов,  принадлежащих  хотя  бы  одному  из  множеств  А  или  В.  Обозначается  .  .  (Рис.  3). 

Рисунок  3.  Объединение  множеств

Разностью  множеств  А  и  В  называется  множество,  состоящее  из  всех  элементов,  множества  А,  не  принадлежащих  множеству  В.  Обозначают  разность  множеств  .  .  (Рис.  4).

Рисунок  4.  Разность  множеств

После  того  как  введены  основные  понятия  и  операции  над  множествами,  необходимо  продемонстрировать  на  практике,  где  применяются  эти  операции.  Доказать  обучающимся,  что  это  не  только  теоретическое  представление.  Например,  очень  наглядно  использование  таких  операций  в  компьютерном  3D-моделировании.  Объяснить,  что  в  различных  современных  программах,  для  3D-моделирования,  таких  как  3ds  Max,  Maya,  Blender  используются  булевы  операции,  привести  примеры  и  выполнить  вместе  не  сложные  упражнения. 

Примеры  упражнений:

1.  По  картинке  определить,  какие  операции  были  применены  к  начальному  множеству.  (Рис.  5).  Чтобы  получить  кусок  сыра,  в  качестве  множеств  нужно  взять  цилиндр  (множество  А),  шар  (множество  В)  и  куб  (множество  С).  Применяя  операцию  разности  к  множествам  А  и  В  получим  дырки.  Затем  применяя  операцию  пересечения  множеств  А  и  С,  получим  кусок  сыра.

Рисунок  5.  Кусок  сыра

2.  В  качестве  еще  одного  упражнения,  предложить  ученикам  создать  новые  объекты  из  предложенных  путем  применения  операций  над  множествами.  Для  демонстрации  можно  использовать  свободный  пакет  Blender  для  создания  трёхмерной  компьютерной  графики,  включающий  в  себя  средства  моделирования  и  анимации.  В  программе  Blender  имеется  встроенный  модификатор  «Boolean»,  позволяющий  выполнять  логические  операции  над  объектами,  а  именно  Intersect  (пересечение  множеств),  Union  (объединение  множеств),  Difference  (разность  множеств). 

Пусть  имеется  набор  стандартных  объектов:  цилиндр,  куб  и  шар.  Используя  логические  операции  получить  такие  объекты:  кольцо,  планету  Сатурн,  кусок  пирога.

Рисунок  6.  Набор  объектов

Каждый  из  предложенных  объектов  является  множеством  с  точки  зрения  теории  множеств.  Чтобы  получить  кольцо,  необходимо  взять  цилиндр  (немного  масштабировать  его)  и  шар.  Затем  получить  разность  этих  множеств.

Рисунок  7.  Поместили  шар  внутрь  цилиндра

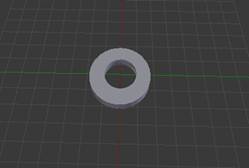
Рисунок  8.  Кольцо.  Использовали  операцию  —  разность  множеств

Для  получения  планеты  Сатурн,  достаточно  поместить  шар  в  центр  кольца  и  применить  операцию  объединения  множеств.  (Рис.  9).

Рисунок  9.  Сатурн.  Использовали  операцию  —  объединение  множеств

Чтобы  получить  кусок  пирога,  будем  использовать  цилиндр  и  куб.

Рисунок  10.  Совместили  часть  цилиндра  и  куба

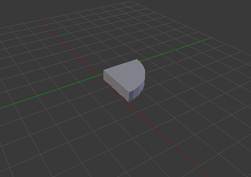
Рисунок  11.  Применили  операцию  пересечения  множеств

3.  Пример  создания  объекта  с  использованием  трех  логических  операций  одновременно.  В  качестве  множеств  использовать  конус,  куб,  шар  и  икосферу.  Для  конуса  и  куба  использовать  операцию  пересечения,  получается  стакан  для  мороженого.  (Рис.  12).  Затем  к  полученному  множеству  и  шару  применяем  операцию  объединения,  получаем  мороженое  в  стаканчике.  Затем  к  последнему  множеству  и  икосфере  применяем  операцию  разности.

Рисунок  12.  Последовательное  применение  операций  пересечения,  объединения  и  разности  к  конусу,  кубу,  шару  и  икосфере  соответственно

Осталось  добавить  цвет  и  немного  сгладить  грани.  Результат  видим  на  рисунке.

Рисунок  13.  Стакан  мороженого

Итак,  можем  видеть,  что  элементы  теории  множеств  могут  применяться  в  компьютерном  моделировании,  для  создания  реальных  объектов.  Такой  подход  к  изучению  материала,  в  большей  степени  заинтересует  учеников.

Список  литературы:

1.Гриншпон  И.Э.,  Киреенко  С.Г.,  Элементы  теории  множеств,  учебное  пособие.  Томск,  2003.  —  42  с.

2.James  Chronister,  Blender  Basics  2.6,  руководство  пользователя.  —  416  с.