МНОГОПРОДУКТОВАЯ МОДЕЛЬ УПРАВЛЕНИЯ ПРОИЗВОДСТВОМ НА ГОРНОДОБЫВАЮЩЕМ ПРЕДПРИЯТИИ

Фокина Мария Сергеевна

магистрант 2 курса, кафедра вычислительной математики и информатики ЮУрГУ, г. Челябинск

Е-mail: f.mariya.s1988@gmail.ru

Панюков Анатолий Васильевич

научный руководитель, д-р физ.-мат. наук, профессор ЮУрГУ, г. Челябинск

Объект исследования — ОАО «Учалинский горно-обогатительный комбинат».

Предмет исследования — оптимальное производство товарной продукции на горнодобывающем предприятии.

Актуальность проблемы. В настоящее время проблемам управления производством уделяется большое внимание. Это связано как с развитием торговли, ростом производства продукции и с необходимостью скорейшего обеспечения потребителей постоянно расширяющимся ассортиментом продукции, так и с большими затратами, вызванными доставкой, хранением и обеспечением потребителей продукцией. Во многих случаях такие затраты удается значительно сократить за счет более успешной организации этих процессов.

Выражение для общих затрат на производство продукции в этом случае имеет следующий вид [1, стр. 2]:

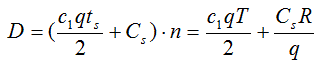
где: c₁ — стоимость производства единицы продукции в единицу времени,

q — объем продукции,

t_s — время между пополнениями,

n=T/t_s=R/q — количество периодов пополнения.

При этом предполагается, что спрос на продукцию постоянен и в течение интервала времени T будет реализовано R единиц продукции.

Оптимальное значение для объема пополняемой продукции q⃰ определяется из условия равенства нулю следующей производной dD/dq= 0.

Решая это уравнение, определяем величину оптимального пополнения запасов q^⃰:

При наличии многих продуктов использование данной формулы становится затруднительным, поскольку для каждого продукта будет определена своя оптимальная величина закупаемого продукта и свое время возобновления поставки. Графически изменение величины производства при таких условиях можно представить в виде, показанном на рисунке 2.

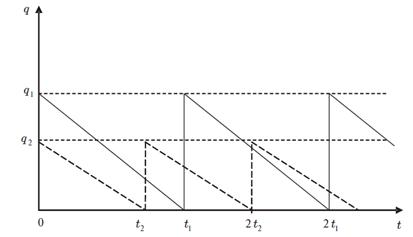
Рисунок 1. График изменения величины производства при использовании формулы Уилсона-Харриса для разных продуктов

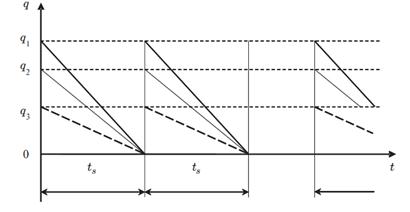
Рисунок 2. График изменения величины производства при одновременной поставке разных продуктов

Для преодоления таких затруднений возникает идея производить продукты нескольких типов одновременно так, чтобы к началу следующего этапа производства предыдущая партия продуктов стала бы равной нулю. Графически процесс изменения величины производства при таком предположении можно представить в следующем виде (рис. 2).

Затраты на производство продукции в течение периода между пополнениями составят:

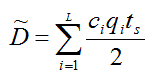
где: L — количество типов продуктов в группе,

q_i — количество единиц i-го продукта,

t_s— интервал времени,

c_i — стоимость производства единицы продукта i-го типа в единицу времени.

Поскольку спрос r_i на i-й продукт постоянен, то объем заказываемой продукции должен быть равен количеству продукции, которое будет израсходовано в течение времени t_s, т. е.   .

Исходя из сделанных предположений, суммарные затраты на хранение и организацию поставки для группы продуктов принимают вид:

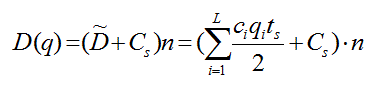
где: n=T/t_s, . Подставив выражения для n и q_i в этом соотношении

Функция D(t_s) является непрерывной функцией t_s, и ее величина стремится к +∞ при t_s →0.

Поэтому минимальное значение функции затрат и соответственно оптимальное значение t_s достигается, когда dD(t_s)/dt_s= 0, т. е. когда

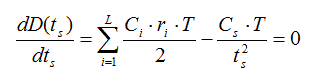
Из этих условий и определяется оптимальное время между смежными пополнениями склада :

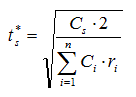
Тогда в соответствии с выражениями, определяющими величины q_i , получим:

Рассмотрим применение изложенного подхода на примере деятельности ОАО «Учалинский горно-обогатительный комбинат».

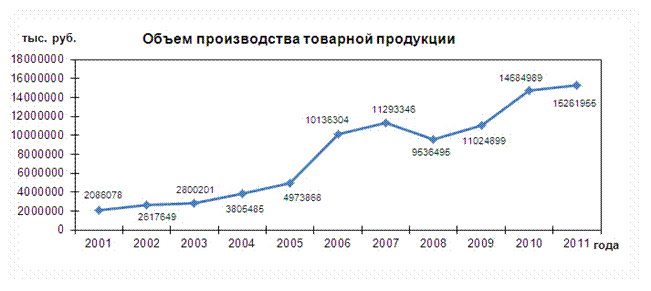Рисунок 3. Объем производства товарной продукции [3]

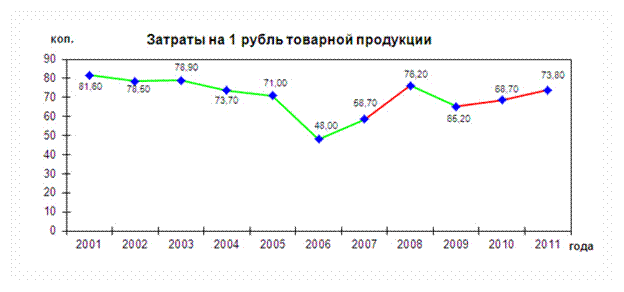
Рисунок 4. Затраты на 1 рубль товарной продукции

Тогда по нашим данным получается:

Средние затраты на производство [2]:

где: ci – затраты на 1 рубль производства меди,

qi – объем производства меди,

ts – промежуток времени

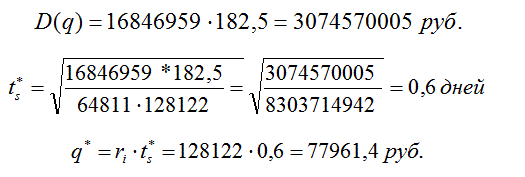
Рассмотрим оптимальный план по производству цинка:

_Р

Таким образом, мы получили: оптимальное количество дней простоя — 1,2; оптимальное производство меди — 77961,4 рублей; оптимальное производство цинка — 17975,66 рублей.

Список литературы:

1.Калинин Н.М. Модели управления многопродуктовыми запасами. / Н.М. Калинин, Е.Н. Хоботов. — Москва: Институт системного анализа РАН. — 15 с.

2.Методические рекомендации «По планированию, формированию, учету затрат на производство и реализацию продукции (работ, услуг) предприятия металлургического комплекса».

3.Официальный сайт ОАО «УГОК». [электронный ресурс] — Режим доступа. — URL: http://ugok.ru (дата обращения 15.12.2012 г)