Статья опубликована в рамках: XXI Международной научно-практической конференции «Проба пера» (Россия, г. Новосибирск, 23 декабря 2015 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ПОВЫШЕНИЕ КАЧЕСТВА МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ
Мельникова Елизавета Владимировна
Ученица 8 «В» класса МБОУ СОШ № 89,
РФ, г. Краснодар
Беспалов Евгений Геннадьевич
научный руководитель: преподаватель математики МБОУ СОШ № 89,
РФ, г. Краснодар
Введение
В современной России школьное математическое образование имеют тенденцию к снижению качества преподаваемого материала. Отсюда, и снижение мотивации учащихся. Я вижу в этом серьёзною проблему для всей системы образования. В данной статье я хочу рассмотреть данную проблему и показать способы повышения качества образования.
Формулировка проблемы
Снижение мотивации учащихся. Проблема заключается в том, что основная масса школьников, не видят в изучаемой дисциплине прикладного значения. Популярен вопрос среди учащихся: «Почему я должен «ломать» голову над сложными примерами и задачами, если не знаю, где это можно применить?».
Пути решения обозначенной проблемы:
Решение поставленной проблемы я, как учитель математики, вижу в «изменении вектора» математического образования среди учащихся средних школ. Я считаю, что необходимо, в первую очередь, в этом вопросе изучить модель школьного образования развитых стран Европы, США и Азии. Изучив, мы увидим, что в данных странах уклон идет не на «сухую» подачу информации, а на возможность учащимися применять полученные знания в повседневности.
Революция в системе школьного образования должна проходить последовательно, логически обоснована. Необходимо учить школьников прикладной математики. Я хочу привести, частично, примеры из своей учительской деятельности. Мои учащиеся, в частности, владеют следующими прикладными темами:
I. Аппроксимация, или приближение – научный метод, состоящий в замене одних объектов другими, в каком-то смысле близкими к исходным, но более простыми.
Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны).
Перед тем, как мы приступили к изучению этой темы, на дополнительных занятиях, я рассказал учащимся где и для чего используются этот метод. Показал примеры. Наиболее подробно мы его изучили, разобрав МНК-метод наименьших квадратов.
1) Метод наименьших квадратов-математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных. Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.
В качестве примера мы рассмотрели таблицу экспериментальных данных. Так как в школьном курсе алгебры не изучаются методы решения систем уравнений с тремя уравнениями и тремя неизвестными (метод Крамера, метод Гаусса, матричный метод и т. д.), то мы ограничились построением линейной зависимости.
Пример 1
В некоторую школу, после её открытия, изначально, поступило 600 учеников. В последующие года число обучающихся учеников приведено в таблице.
Таблица 1.
Количественное распределение учеников за первые 7 лет с момента открытия школы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение
МНК даёт нам возможность построить функциональную зависимость с целью приблизительного, почти точного, прогноза количества поступающих учащихся в последующие годы.
Линейная зависимость имеет вид: y=ax+b. N=7
Коэффициенты a и b можно найти, решив простейшую систему уравнений:

Таблица 2.
Необходимая для расчётов по методу НК информация
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда, наша система уравнений примет следующий вид:
![]()
Решим данную систему методом сложения, домножив второе уравнение на -4 и сложив, почленно, оба уравнения:
![]()
![]()
28a=242
a=8.642
b=627.861
Следовательно, линейная зависимость имеет вид: y=8.642x+627.861
Построим график зависимости. Нанесем экспериментальные точки.

Рисунок 1. Линейная аппроксимационная зависимость
Рассмотренный пример помогает понять, как метод наименьших квадратов, который включает в себя аппроксимацию, помогает делать статистические прогнозы.
Рассмотренный метод может быть использован школьниками в следующих изучаемых дисциплинах:
1) Физика-по экспериментальным данным построение собственного прогноза появления значения изучаемой величины
2) Химия-по аналогии с физикой, так же, можно строить прогнозы.
3) Биология-прогнозирование увеличения (уменьшения) численности какого-либо представителя животного мира.
II. Задачи на нестандартное решение.
Не менее важен и интересен этот пункт. Большинство задач, входящих в школьные учебники математики, имеют алгоритмических характер, т. е. решаются по подобию, путем построения определённой, базовой математической модели. И здесь, есть две проблемы: либо, эти задачи «приедаются» школьникам своею однообразностью и «нереальностью» условий, либо эти задачи слишком сложны для восприятия учащимися и построения математической модели по условию. Но, следует отметить очень важный факт: перечисленные категории задач являются обязательными к изучению. Никуда от этого не деться. Но, можно и нужно учебный процесс разнообразить нестандартными задачами с интересными формулировками. Для своих учеников я стараюсь подбирать такие задачи на каждый урок. И, в конце урока я зачитываю им эти задачи и ставлю условия, для выработки мотивации и соперничества.
Моя любимая задача формулируется так: «Если полторы курицы откладывают полтора яйца за полтора дня, то сколько кур отложат шесть яиц за шесть дней?»
Сразу бросается в глаза, что имеются три зависящие друг от друга величины: число кур(К), число дней(Д), число яиц(Я). И, здесь начинается самый интересный и сложный для школьников момент: как связать начальные условия и вопрос, поставленный в задаче? Задача педагога научить детей связывать с помощью дополнительного параметра два условия. Таким параметром, в нашей задаче, будет являться продуктивность одной курицы.
![]()
Отсюда, подставив начальные значения, найдем, продуктивность П=![]() .
.
Далее, выразим из формулы продуктивности переменную К. Имеем:
![]()
Подставив все значения (Я=6, Д=6, П=![]() ) мы получим результат К=
) мы получим результат К=![]() . То есть, полторы курицы за шесть дней снесут 6 яиц с продуктивностью П=
. То есть, полторы курицы за шесть дней снесут 6 яиц с продуктивностью П=![]() .
.
Подобные задачи с большим успехом обучают школьников мыслительной, логической способности связывать, вводя новые переменные, начальные и конечные, два или более условий.
III. «Из сложного в увлекательное»
Я неспроста именно так назвал третий пункт своей статьи. В нём я хочу показать, как можно заинтересовать старшие классы изучением сложных разделов математического анализа. Для этого, необходимо представлять сложные математические понятия на простых «житейских» примерах. Например, рассмотрим следующую задачу.
Задача
Допустим, у вас заслуженный отдых. Море. Пляж. Вы лежите, загораете. В руке у вас банка с холодной газированной водой. Вы ставите ее на песок и……она опрокидывается. Что делать? И тут, вы начинаете понимать, задаваться вопросом: банка не упала бы, если центр тяжести находился бы в самом низу. И тут, вас осенило: «Да это же задача на экстремум, с очень простой формулировкой: «При каком уровне воды в банке центр тяжести лежит ниже всего?» Подумаем…..». И так, давайте будем рассуждать. Ограничимся вертикальным разрезом банки, имеющим форму прямоугольника. Центр тяжести самой банки ![]() лежит точно в центре этого прямоугольника, а центр тяжести воды
лежит точно в центре этого прямоугольника, а центр тяжести воды ![]() лежит в центре меньшего прямоугольника, высота которого равна высоте x воды в банке. Если принять высоту банки за единицу измерения, то центры тяжести
лежит в центре меньшего прямоугольника, высота которого равна высоте x воды в банке. Если принять высоту банки за единицу измерения, то центры тяжести ![]() и
и ![]() лежат на высотах
лежат на высотах ![]() и
и ![]() соответственно. При этом, заметим, что буква x выбрана не случайно, так как высота уровня воды-единственная величина, которая здесь может изменяться.
соответственно. При этом, заметим, что буква x выбрана не случайно, так как высота уровня воды-единственная величина, которая здесь может изменяться.
Где расположен центр тяжести всей банки, включая воду? Нужно воспользоваться тем же правилом, которое используют, например, астрономы для того, чтобы определить центр тяжести системы из двух звёзд: центр тяжести системы расположен на линии, которая соединяет центры тяжести каждой из звёзд. При этом, важно отметить, что расстояния от общего центра тяжести до центров тяжести обеих звёзд обратно пропорциональны массе звёзд: чем звезда тяжелее, тем ближе к ней общий центр тяжести.
При этом
![]()
Пусть масса пустой банки ![]() Содержимое пол-литровой банки весит
Содержимое пол-литровой банки весит ![]() В частично наполненной банке –x, умноженное на 500 г. Выражение
В частично наполненной банке –x, умноженное на 500 г. Выражение ![]() в нашем случае равно разнице между
в нашем случае равно разнице между ![]() и
и ![]() , то есть
, то есть ![]()
В результате, имеем:

Решим это уравнение относительно ![]() :
:
![]()
Чтобы теперь найти высоту s(x) центра тяжести, надо к величине ![]() прибавить высоту центра тяжести воды, то есть
прибавить высоту центра тяжести воды, то есть ![]() :
:
![]()
Значит, по условию задачи, необходимо найти минимум функции
![]()
По правилам дифференцирования, производная этой функции будет являться производной от частного:
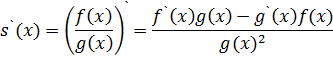

Если привести подобные члены и сократить, остаётся
![]()
Нас интересуют только значения x, при которых эта функция равна нулю. Для этого должен быть равен нулю числитель дроби:
![]()
Разделив это уравнение на 200, получим простое квадратное уравнение:
![]()
Отсюда: ![]()
Получаем два решения, из которых, однако, одно отрицательное, которое нас не интересует, так как содержание воды в банке число положительное. Остаётся одно решение:
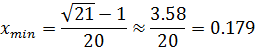
То есть, при уровне воды в банке, равном, 0,179 метра, центр тяжести будет лежать ниже всего. Вывод: банка будет находиться в устойчивом положении.
Приведённая задача взята мною из замечательной книги немецкого журналиста Кристофа Дрёссера. Таких задач существует великое множество. Я считаю их очень полезными для учащихся потому, что:
1) Они избавляют большой процент школьников от стереотипа «математика – скучный, сложный и неинтересный предмет». И, как следствие, сложные, изучаемые по школьному курсу алгебры темы, приобретают увлекательный характер.
2) Школьники учатся использовать приобретённые на уроках математики знания в быту. Это очень важно. Это тот курс, к которому должна быть «повёрнута» система образования в РФ.
Помимо приведённых выше пунктов, школьников необходимо, также, знакомить и с историей математики, показывать примеры «математика в искусстве», например, Золотое Сечение, про которое можно очень многое рассказать и показать.
Моя задача, как учителя математики средней общеобразовательной школы проста: «Я должен показать детям, ученикам всю красоту математики, показать, что всё, что они видят, чем пользуются, всё это есть набор математических формул и операторов». Из этого всего они могут сделать вывод: «Математика-по праву называется «Царицей наук». Не поняв её, не поймешь, по каким законам функционирует весь окружающий нас мир и вся Вселенная……»
Список литературы:
- Сайт [Электронный ресурс] – режим доступа. – URL: https://ru.wikipedia.org/wiki.
- Сайт [Электронный ресурс] – режим доступа. – URL: http://www.cleverstudents.ru/articles/mnk.html
- «Обольстит математикой» Кристоф Дрёссер.
дипломов

Оставить комментарий