МАГИЧЕСКИЕ  ТРЕУГОЛЬНИКИ

Долгоруков  Михаил

класс  4  «В»,  лицей  им.  М.В.  Ломоносова,  РФ,  г.  Йошкар-Ола

Салихова  Лилия  Марсельевна

научный  руководитель,  ст.  преп.  кафедры  Прикладной  математики,  ФГБОУ  ВПО  «ПГТУ»,  РФ,  г.  Йошкар-Ола

Цель  работы: 

1.  Познакомиться  с  магическими  треугольникамими.

2.  Узнать  историю  возникновения  треугольников.

3.  Научиться  правильно  и  быстро  заполнять  магические  треугольники.

4.  Узнать,  знакомы  ли  мои  одноклассники  с  чудесными  треугольниками. 

5.  Познакомиться  с  учёными,  которые  приложили  немного  труда  для  изучения  математики.

Геометрия  —  это  одна  из  древнейших  наук.  Ее  история  насчитывает  не  одно  тысячелетие.  Исследовать  различные  пространственные  формы  издавна  побуждало  людей  их  практическая  деятельность.  Древнегреческий  ученый  Эвдем  Родосский  в  IV  веке  до  нашей  эры  писал:  «Геометрия  была  открыта  египтянами,  и  возникла  при  измерении  Земли.  Это  измерение  было  им  необходимо  вследствие  разлития  реки  Нил,  постоянно  смывавшей  границы».  Как  наука,  геометрия  впервые  сформировалась  в  Древней  Греции.  Треугольник  является  незаменимой  фигурой  во  всей  геометрии,  так  как  именно  он  лежит  в  основе  этой  науки. 

Простейший  из  многоугольников,  треугольник,  играет  в  геометрии  важнейшую  роль.  Треугольник  был  сначала  обычной  геометрической  фигурой  на  плоскости,  которую  маглы  использовали  в  разных  целях.  Одна  из  таких  целей  —  земледелие.  Например,  в  древности  участки  делили  таким  образом:  выбирали  три  произвольные  точки  и  соединяли  их  линиями.  Так  и  появились  первые  треугольники.

Треугольник  является  также  одной  из  первых  геометрических  фигур,  которая  стала  использоваться  в  орнаментах  древних  народов.  В  Древнем  Египте  он  был  прямоугольным  и  являлся  воплощением  триады  духовной  воли,  любви  и  высшего  разума  человека.  Перевернутый  треугольник  у  многих  народов  был  символом  сердца,  символом  жертвенной  чаши  —  в  Индии,  символом  внутреннего  мира  человека  —  в  древней  Руси,  На  Древнем  Востоке  треугольник  с  вершиной,  соединенной  с  такой  же  геометрической  фигурой,  использовали  в  качестве  эмблемы  временного  цикла.

Фигуры  называют  магическими,  если  числа,  нужные  для  их  заполнения  размещены  так,  что  в  каждом  горизонтальном,  вертикальном  и  диагональном  ряду  получается  одна  и  та  же  сумма. 

Магические  фигуры  делятся  на  плоские  и  пространственные,  так  как  существуют  магические  квадраты,  треугольники,  прямоугольники,  многоугольники  и  круги,  а  также  и  магические  кубы. 

Магическим  треугольником  называется  такое  размещение  шести  натуральных  чисел  в  вершинах  и  серединах  сторон  треугольника,  при  котором  суммы  чисел  на  каждой  из  сторон  равны  между  собой.  Пример  магического  треугольника  приведен  на  рисунке  1.

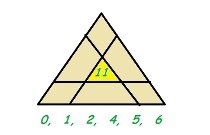
Рисунок  1.  Пример  магического  треугольника

После  того,  как  все  цифры  в  треугольнике  будут  расставлены  на  свои  места,  получается  следующий  вид  (см.  рис  2).

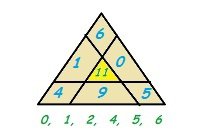
Рисунок  2.  Решенный  магический  треугольник

Существуют  различные  классификации  магических  треугольников.  Изучив  особенности  и  обобщив  научные  сведения  об  этих  магических  фигурах,  можно  сказать,  что  именно  они  являются  основным  составляющим  головоломок  и  задач  на  сообразительность. 

Для  тех,  кто  заинтересовался  данными  треугольниками  ниже  приведены  задачи  для  решения.

1.  Реши  магический  треугольник.  Сумма  цифр  вдоль  каждой  стороны  треугольника  должна  быть  равна  12.  Используй  цифры  внизу  рисунка.  Повторяться  они  не  должны. 

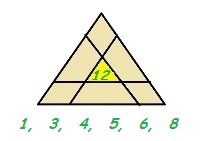
Рисунок  3.  Рисунок  к  задаче  1

2.  Реши  магический  треугольник.  Сумма  цифр  вдоль  каждой  стороны  треугольника  должна  быть  равна  числу  в  середине.  Используй  цифры  внизу  рисунка.  Повторяться  они  не  должны. 

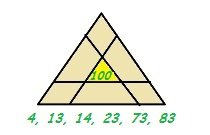
Рисунок  4.  Рисунок  к  задаче  2

3.  В  данном  треугольнике  имеются  з  треугольника  поменьше,  содержащие  каждый  по  4  маленьких.  Если  большой  треугольник  является  магическим,  то  сумма  чисел  в  треугольниках  поменьше  равна  какому-то  одному  числу.  Расставьте  числа  0,2,3,4,5,6,8,9,12  в  соответствии  с  правилами  магического  треугольника  так,  чтобы  сумма  чисел  в  каждом  треугольнике  поменьше  была  равна  18.

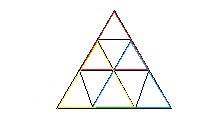
Рисунок  5.  Рисунок  к  задаче  3

Список  литературы:

1.Волина  З.В.  «Веселая  математика»  М.,  1999  г.

2.Перельман  Я.И.  Живая  математика.  Математические  рассказы  и  головоломки.  М.:  Мир  энциклопедий  Аванта+,  Астрель,  2008.  —  271  с.