КРИВЫЕ  ВРАЩЕНИЯ  ГАЛАКТИК

Садовников  Никита

Класс  11  «Б»,  гимназия  №  11,  г.  Волгоград

Быкова  Виктория  Ивановна

научный  руководитель,  педагог  первой  категории,  учитель  физики,  гимназия  №  11,  г.  Волгоград

Основная  задача  звездной  динамики  —  изучение  движения  большого  числа  объектов,  составляющих  галактики  или  звездные  скопления,  требует  решения  главной  проблемы:  определение  скоростей  звезд,  движущихся  в  гравитационном  поле,  создаваемым  массами  с  заданным  распределением  [4].

В  решении  данной  проблемы  достигнут  существенный  прогресс,  однако,  она  не  утратила  своей  актуальности,  далека  от  окончательного  решения  и  по-прежнему  вызывает  интерес.  В  данной  работе  предпринята  попытка  построения  кривой  вращения  галактики  с  заданным  распределением  масс  и  сравнение  ее  с  наблюдаемыми  кривыми  вращения  спиральных  галактик.  Исследуется  многокомпонетная  модель,  состоящая  из  сферического  балджа,  звездно-пылевого  диска  и  темной  короны  (гало).  Распределение  масс  каждого  компонента  определяется  законом  уменьшения  плотности  с  расстоянием.  Соответствие  модельных  кривых  вращения  наблюдаемому  многообразию  кривых  вращения  спиральных  галактик  может  быть  достигнуто  вариацией  небольшого  числа  параметров  (по  два  для  каждого  компонента).

Актуальность.  Кривая  вращения  галактики  позволяет  оценить  ее  общее  гравитационное  поле,  создаваемое  массой  различных  сред,  входящих  в  состав  галактики  —  звездами,  газом,  пылью.  Далее,  анализируя  поле,  удерживающее  и  газ,  и  звезды,  можно  узнать,  как  масса  распределена  в  галактике.  Таким  образом,  зная  изменение  с  расстоянием  круговой  скорости  вращения  объектов  в  галактике  можно  попытаться  восстановить  распределение  плотности  вещества  в  ней,  как  видимого,  так  и  невидимого,  но  создающего  поле  тяготения.

Цель  данной  работы  —  исследовать  особенности  поведения  кривой  вращения  галактики  при  различных  законах  распределении  звездной  плотности  входящих  в  ее  состав  компонентов.

Объект  работы  является  спиральная  галактика  и  ее  составляющие:  балдж,  гало  (корона),  звездный  диск.

Предметом  исследования  является  построение  графиков,  описывающих  зависимость  круговой  скорости  вращения  галактических  объектов  от  расстояния  от  центра  средствами  Microsoft  Excel.

Практическая  значимость  работы  заключается  в  том,  что  построение  кривой  вращения  галактики  по  известному  распределению  масс  позволяет  глубже  понять  динамические  процессы,  в  которых  принимают  участие  звезды  в  галактике,  а  также  применять  данный  материал  и  полученные  результаты  для  внеурочной  работы  по  физике  и  астрономии  в  школе.

Оценка  распределения  массы  по  вращению  галактики

Эффективным,  но  не  однозначным,  методом  определения  массы  галактики  и  решения  вопроса  о  плотности  и  характере  распределения  вещества  внутри  галактики  является  метод,  основанный  на  измерении  скорости  вращения  галактики  [7].  Метод  не  сложнее  определения  массы  Солнца  по  скоростям  орбитального  движения  планет.  Если  Солнце  вдруг  станет  массивнее,  то  Земле  придется  двигаться  быстрее  по  орбите,  в  противном  случае  она  упадет  на  Солнце.  Менее  массивное  Солнце  с  меньшей  силой  гравитационного  притяжения  означало  бы  необходимость  более  медленного  движения  Земли,  в  противном  случае  она  улетела  бы  в  космическое  пространство.  Таким  образом,  скорость  движения  Земли  по  орбите  в  точности  соответствует  значению  для  устойчивой  орбиты  вокруг  звезды  с  массой  в  одну  солнечную.

Точно  так  же  Солнце  и  другие  звезды  движутся  по  орбитам  вокруг  центра  нашей  Галактики  со  скоростями,  определяемыми  ее  массой.  Если  измерить  скорость  и  определить  размер  орбиты,  то  можно  вычислить  массу,  управляющую  орбитой.  Но  имеется  существенное  отличие  движения  в  планетной  системе,  у  которой  практически  вся  масса  сосредоточена  в  центральной  звезде,  и  в  галактике,  где  вещество  распределено  в  большом  объеме.

Это  значит,  что  общую  массу  галактики  можно  определить  лишь  по  скоростям  звезд  во  внешних  частях,  для  которых  вся  галактика  находится  внутри  орбиты  звезды.

Графически  зависимость  круговой  скорости  вращения  галактики  от  расстояния  от  центра  выражается  кривой  вращения.  Такой  подход  позволяет  по  известной  кривой  вращения  галактики  оценить  ее  общее  гравитационное  поле,  создаваемое  массой  различных  сред,  входящих  в  состав  галактики  —  звездами,  газом,  пылью.  Далее,  анализируя  поле,  удерживающее  и  газ,  и  звезды,  можно  узнать,  как  масса  распределена  в  галактике.  Таким  образом,  зная  изменение  с  расстоянием  круговой  скорости  вращения  объектов  в  галактике  можно  попытаться  восстановить  распределение  плотности  вещества  в  ней,  как  видимого,  так  и  невидимого,  но  создающего  поле  тяготения.  Внутри  кривой  скорости  звезд  увеличиваются  по  мере  удаления  от  центра  (рис  1.). 

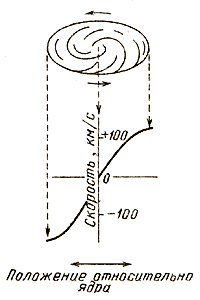
Рисунок  1.  Кривая  вращения  звезд  галактики

Потом  скорость  выходит  на  постоянный  уровень,  после  чего  кривая  вращения  начинает  падать.  За  точкой  поворота  все  скорости  должны  дать  величину  массы  галактики.  Для  большей  точности  астрономы  подгоняют  под  весь  набор  скоростей,  измеряемых  при  различных  положениях,  разные  модели  распределения  массы  в  галактике,  узнавая,  таким  образом,  кое-что  об  этом  распределении,  а  также  значение  общей  массы.

На  рис.2  приведены  кривые  вращения  галактик  типа  Sb

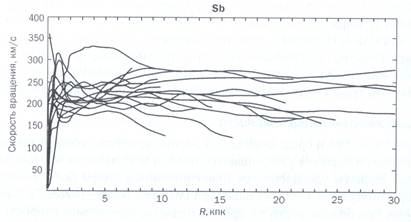
Рисунок  2.  Вид  кривых  вращения  галактик  типа  Sb

В  60-е  годы  эти  исследования  велись  весьма  интенсивно.  Для  всех  типов  было  впечатление,  будто  кривая  вращения  загибается  вниз  вблизи  границы  наблюдаемой  области.  Кривые  хорошо  согласовывались  с  моделями  распределения  массы,  и  распределение  вещества  в  галактиках  выглядело  весьма  разумным.

Моделирование  кривых  вращения  галактик

Для  проведения  расчетов  построения  кривой  вращения  галактики  необходимо  использовать  удобную  систему  единиц.  Рассмотрим  характерные  значения  масс,  расстояний,  скоростей,  определяющих  галактики  и  движение  звезд  в  них.  Воспользуемся  данными  из  справочника  Аллена  [1]:

Масса  Солнца  ,  1  парсек  , 

За  единицу  массы  примем  массу  типичной  галактики:  ,  за  единицу  расстояния  —  1  килопарсек  (кпк): 

,  —  где  G*  модифицированная  постоянная  тяготения  в  новой  системе  единиц     

Рассмотрим  простые  модели  распределения  вещества  галактики,  составляющими  которой  являются  1)  балдж,  2)  диск,  включающий  помимо  звезд  пыль  и  газ,  3)  корону  (гало). 

Кривые  вращения  спиральных  галактик

Балдж

В  ходе  исследования  мы  рассмотрели  модель  распределения  плотности,  отвечающей  эмпирической  степенной  зависимости  [5]:

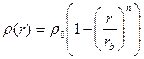                                       (1)

При  показателе  степени    получается  линейное  падение  плотности  к  внешней  границе  балджа  (),  а  при    —  однородное  распределение  плотности  звезд  внутри  объема  балджа.  Масса  вещества  балджа  ,  заключенная  внутри  сферы  радиуса  r,  равна  [3]

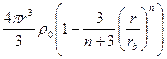=                                 (2)

Полная  масса  балджа

                       (3)

После  подстановки  (3)  в  (2)  получим

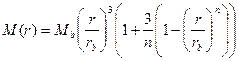                               (4)

Круговые  скорости  звезд  находились  из  соотношения 

   (км/с)                                      (5)

Расчет  проводился  с  помощью  математического  приложения  Excel.  Параметры  моделей  выбирались  следующим  образом:  масса  балджа  (в  условных  единицах  М₀)  изменялась  ,  а  параметр  в  законе  распределения  плотности  (1)  .  Радиусы  балджа  принимались  равными    кпк.

Примеры  расчетов  скоростей  приведены  в  таблице  1  и  2.  Графики  зависимости  скорости  балджа  Vr  от  расстояния  r  представлены  на  рис.3,  4

Таблица  1. 

Зависимости  скоростей  балджа  при  различных  параметрах  n  (rb=1,  M=0,001)

Таблица  2. 

Зависимости  скоростей  балджа  при  различных  параметрах  n  (rb=2,  M=0,05)

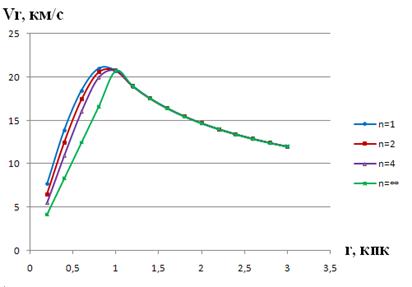
Рисунок  3  График  зависимости  скорости  балджа  Vr  от  расстояния  r  при  rb=1,  M=0,001

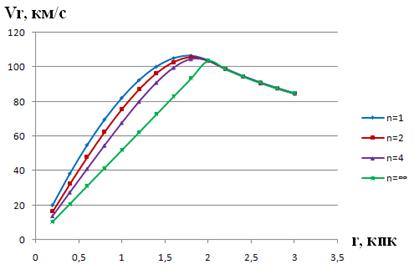
Рисунок  4.  График  зависимости  скорости  балджа  Vr  от  расстояния  r  при  rb=2,  M=0,05

Звездный  диск

Для  плоских  дисковых  систем  вычисление  распределения  гравитационного  поля  является  сложной  задачей.  В  системе  со  сферически  симметричным  или  эллиптичным  распределением  плотности  на  каждую  точку  действует  только  масса,  заключенная  внутри  сферы  (эллипсоида),  проходящей  через  нее.  Для  диска  же  создаваемое  гравитационное  поле,  а,  следовательно,  и  круговая  скорость  на  данном  расстоянии  от  центра  зависят  от  массы  не  только  внутри  данного  радиуса,  но  и  за  его  пределами.  При  моделировании  галактик  часто  используют  тонкий  диск  [5]  с  экспоненциальным  распределением  по  радиусу  поверхностной  звездной  плотности:  ,  где  a  составляет  несколько  килопарсек.  Кривая  вращения  диска    вычисляется  только  с  использованием  высшей  математики  [2].  Сначала  скорость  нарастает,  достигает  максимального  значения  V_m  при  R_m,  а  затем  плавно  спадает.  Величины  V_m  и  R_m  определяются  через    и  массу  диска  M_d  соотношениями

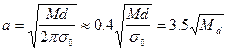                               (6)

                                          (7)

                                                   (8) 

        (9)

Для  расчетов  мы  использовали  два  значения  плотности:    и 

Кривые  вращения  диска  получались  путем  пропорционального  растяжения  и  сжатия  по  осям  R  и  V  (см.  рис.  5)

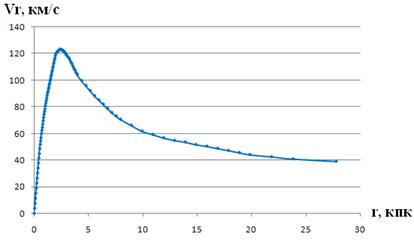
Рисунок  5.  График  зависимости  скорости  звездного  диска  Vr  от  расстояния  r  при  M=0.1,  σ=0,013ρ₀

Галактическое  гало

Закон  для  распределения  яркости  у  эллиптических  галактик  Кинг  предложил  рассмотреть  в  виде  [5]

       ,                                     (10)

где  параметр  а  соответствует  радиусу,  на  котором  яркость  составляет  половину  от  центральной,  и  показал,  что  соответствующий  ему  закон  распределения  пространственной  плотности  звездной  материи:

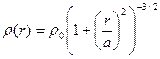.                                   (11)

В  той  же  работе  приведено  выражение  для  соответствующей  этой  плотности  массе  вещества  гало,  заключенной  внутри  сферы  радиуса  r:

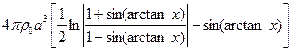=                  (12)

Для  галактики,  подобной  нашей,  радиус  ее  видимого  диска  составляет  ,  масса  видимой  составляющей  ,  или  .  Как  показывают  расчеты  [3]  масса  гало  на  таком  расстоянии  должна  составлять  около  100%  массы  видимого  вещества.  Действие  гало  начинает  проявляться  на  расстоянии  6—8  кпк. 

1)                    Пусть  параметр  =8  кпк. 

На  границе  видимой  части  галактики  .  Отсюда  получим,  что  плотность  вещества  гало    .    

Масса  внутри  сферической  части  гало  радиуса  r 

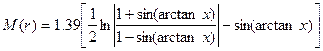                      (13)

Круговые  скорости  находились  по  формуле  .

Результаты  расчета  круговых  скоростей  для  гало  показали  следующее:  плотность  вещества  гало,  согласно  предложенному  Кингом  соотношению  (12),  спадает  пропорционально  ,  объем  растет  как  ,  следовательно,  масса  почти  не  увеличивается.  Всю  ожидаемую  массу  (М=1)  гало  собирает  при  ,  расчетные  круговые  скорости  звезд  достигают  140  км/с  и  медленно  падают  с  расстоянием.

2)                    При  a=20  кпк 

  и 

Массу  (М=1)  гало  собирает  при  ,  расчетные  круговые  скорости  звезд  медленно  нарастают  с  расстоянием.  Эта  модель  более  физически  справедлива  и  отвечает  наблюдениям. 

Конечные  скорости  гало  при  различных  параметрах  представлены  в  таблице  3

Таблица  3. 

Зависимости  скоростей  гало  при  различных  параметрах

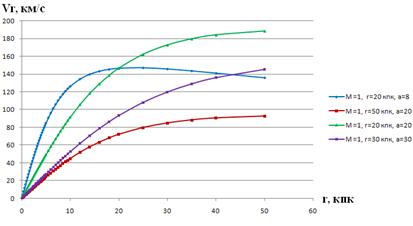
Рисунок  6  Графики  зависимости  скорости  гало  Vr  от  расстояния  r  при  различных  параметрах

Приведенные  оценки  вполне  пригодны  для  величины  массы  реальных  галактик,  в  которых  во  внутренних  частях  доминирует  диск.  Но  в  общем  случае  требуется  учет  других  составляющих.  Поэтому  модели  галактик,  как  правило,  бывают  многокомпонентные.

,

т.  е.  при  построении  кривой  вращения  галактики  суммируются  квадраты  круговых  скоростей,  обусловленные  различными  компонентами. 

Таблица  4. 

Многокомпонентная  модель  галактики-1

Таблица  5. 

Многокомпонентная  модель  галактики-2

Модельные  кривые  вращения  галактики-1  и  галактики-2  приведены  на  рис.7,  8  соответственно

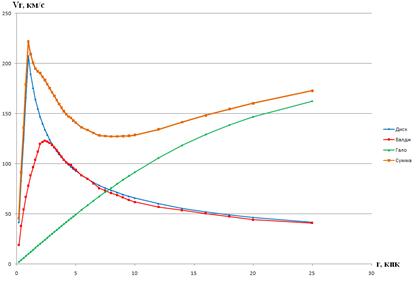
Рисунок  7.  Модельная  кривая  вращения  галактики-1

Рисунок  8.  Модельная  кривая  вращения  галактики-2.  Показан  вклад  отдельных  составляющих  –  звездного  диска,  балджа  и  темного  гало

Выводы:

1.  Смоделировано  движение  звезд  в  спиральной  галактике  с  известным  распределением  масс  с  учетом  трех  компонентов  (диск,  балдж  и  гало).

2.  Показано,  что  вариацией  ограниченного  количества  свободных  параметров  модели  для  трех  компонентов  (балдж,  диск,  гало)  можно  добиться  соответствия  смоделированной  кривой  и  наблюдаемой  кривой  вращения  галактики. 

Список  литературы:

1.Аллен  К.У.  Астрофизические  величины.  /Пер.  с  англ.,  М:  «Мир»,  1977.  —448  с.

2.Астрономия:  Век  XXI,  /Ред.  В.Г.  Сурдин,  -  Фрязино:  «Век  2»,  2007.  —  608  с.

3.Итоги  науки  и  техники.  Астрономия.  Т.26/под  ред.  Т.А.  Агекяна.  М.:  Винити,  1985.  —156  с.

4.Засов  А.В.,  Постнов  К.А.  Общая  астрофизика.  Фрязино:  «Век  2»,  2006.  —496  с.

5.Кинг  А.Р.  Введение  в  классическую  звездную  динамику:  учебное  пособие.  /Пер.  с  англ.  В.Г.  Сурдина  и  А.С.  Расторгуева.  М.:  Едиториал  УРСС,  2002.  —  496  с.

6.Классификация  галактик  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.gect.ru/astronomy/typesgal.html  (Дата  обращения:  октябрь  2012).

7.Моделирование  кривых  вращения  галактик  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.astronet.ru/db/msg/1213793/node7.html  (Дата  обращения:  ноябрь  2012).