КРИВАЯ  ВТОРОГО  ПОРЯДКА  И  ШКОЛА

Губайдуллина  Лейсан

класс  8  «А»  МБОУ  «Гимназия  №  10»,  г.  Казань

Замалиева  Талия  Гайнутдиновна

научный  руководитель,  педагог  высшей  категории,  преподаватель  математики  МБОУ  «Гимназия  №  10  «,г.  Казань

В  настоящее  время  отмечается  спад  мотивации  в  изучении  естественнонаучных  дисциплин,  в  том  числе  геометрии.  Одной  из  причин  является  отсутствие  наглядных  пособий,  связи  изученного  материала  с  жизнью,  истории  возникновения  той  или  иной  кривой. 

Цель  данной  работы  заключается  в  разработке  и  внедрении  в  учебный  процесс  интересующих  ребят  моментов  урока,  а  именно  при  изучении  графика  обратной  пропорциональности  —  гиперболы.

Еще  в  глубокой  древности  греки  получали  кривые,  пересекая  прямой  круговой  конус  плоскостью.  Если  взять  тупоугольный  конус  и  разрезать  его  перпендикулярно  к  образующей,  то  сечение  при  этом  дает  гиперболу.  Отсюда  произошли  и  названия  кривых,  которые  были  введены  Апполонием  Пергским;  гипербола  означает  преувеличение,  перевес  (угла  конуса  над  прямым).  Позже  греки  увидели,  что  все  три  кривые  можно  получить  на  одном  конусе,  изменяя  наклон  секущей  плоскости.  При  этом  конус  следует  брать  двуполостный  и  мыслить,  что  он  простирается  в  обе  стороны  бесконечно.

Одна  и  та  же  линия  в  различных  системах  координат  представляется  различными  уравнениями.

Любую  новую  систему  прямоугольных  декартовых  координат  x^*0y^*  можно  получить  из  любой  старой  системы  x0y  с  помощью  двух  движений:

1.  параллельным  переносом; 

2.  поворотом  вспомогательной  системы  вокруг  точки  0^*  до  совмещения  с  новой  системой  x^*0y^*.

Уравнение    называется  каноническим  уравнением  гиперболы.  Название  «каноническое»  —  греческое  слово  означает  принятое  в  качестве  образца,  типовое.

Две  гиперболы,  которые  определяются  уравнениями: 

  и  ,

при  одних  и  тех  же  значениях  параметров  a  и  b  называются  сопряженными.

Если  действительная  и  мнимая  оси  равны  (a=b),  то  гипербола  называется  равносторонней  (или  равнобочной).  Уравнение  имеет  такой  вид:

В  результате  поворота  осей  системы  координат  x0y  вокруг  начала  координат  0  на  угол  a=-45⁰ получаем  уравнение  равносторонней  гиперболы,  отнесенной  к  своим  асимптотам x^*=0; y^*=0 в  новой  системе  координат  x^*0y^*,  который  представляет  собой  график  обратной  пропорциональности  ,  где  k  —  постоянная  величина.

Далее  можно  рассмотреть  2  способа  построения  гиперболы  и  применение  уравнения  равносторонней  гиперболы,  графика  обратной  пропорциональности  при  решении  задач  из  жизни.

1.Рассмотрим  задачу  на  применение  гиперболы.  Две  железнодорожные  станции  А  и  В  находятся  на  расстоянии  l  км  одна  от  другой.  В  точку  М  груз  можно  доставить  со  станции  А  либо  по  прямой  автотранспортом,  либо  по  железной  дороге  до  станции  В,  а  оттуда  автомобилями  (рис.  1).  При  этом  железнодорожный  тариф  (цена  перевозки  одной  тонны  на  1  км)  составляет  m  рублей,  погрузка-разгрузка  обходится  в  k  рублей  (за  1  т)  и  тариф  автотранспорта  —   n  рублей    Определим  так  называемую  зону  влияния  железнодорожной  станции  В,  то  есть  ту  зону,  в  которую  дешевле  доставить  груз  из  А  смешанным  путем:  по  железной  дороге  и  затем  автотранспортом.

Решение.  Стоимость  доставки  1  т  груза  по  пути  АМ  составляет  r_an  где  r_a=AM,  а  по  пути  ABM  она  будет  равна    Нам  надо  решить  двойное  неравенство    и  определить  ,  как  распределятся  точки  на  плоскости  (x,y)  ,  в  которые  дешевле  доставлять  груз  либо  первым,  либо  вторым  путем.

Найдем  уравнение  линии,  образующей  границу  между  этими  двумя  зонами,  то  есть  геометрическое  место  точек,  для  которых  оба  пути  равно  выгодны:

 .

 Из  этого  условия  получаем:

Следовательно,  линия  раздела  —  гипербола.  Для  всех  внешних  точек  этой  гиперболы  более  выгоден  первый  путь,  а  для  внутренних  —  второй.  Поэтому  гипербола  и  очертит  зону  влияния  станции  В.  Вторая  ветвь  гиперболы  очертит  зону  влияния  станции  А  (груз  доставляется  со  станции  В).  Найдем  параметры  нашей  гиперболы,  Ее  большая  ось:

а  расстояние  между  фокусами  (которыми  являются  станции  А  и  В  )  в  данном  случае  2c=1.

Таким  образом,  условие  возможности  этой  задачи,  определяемое  соотношением  ,  будет:

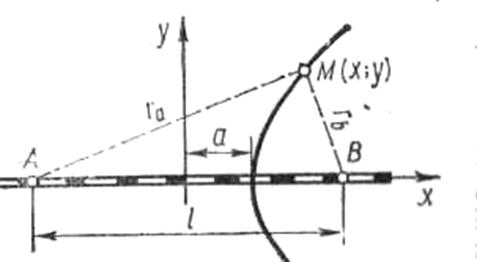
Рисунок  1.  Применение  гиперболы  в  жизни

2.  Мощность  отопителя  в  автомобиле  регулируется  дополнительным  сопротивлением,  которое  можно  менять,  поворачивая  рукоятку  в  салоне  машины.  При  этом  меняется  сила  тока  в  электрической  цепи  электродвигателя  —  чем  меньше  сопротивление,  тем  больше  сила  тока  и  тем  быстрее  вращается  мотор  отопителя.  На  рисунке  2  показана  зависимость  силы  тока  от  сопротивления.  На  оси  абсцисс  откладывается  сопротивление  в  (омах).  На  оси  ординат  —  сила  тока  в  амперах.  На  сколько  ампер  уменьшится  сила  тока,  если  увеличить  сопротивление  с  1  Ом  до  1,5  Ом?

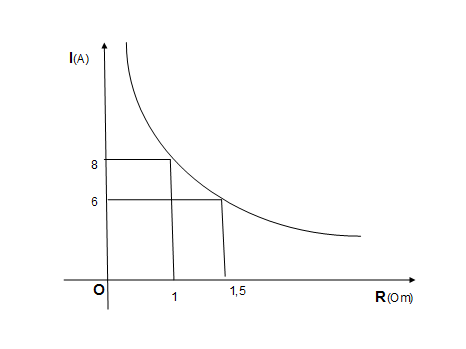
Рисунок  2.  Гипербола  в  области  физики

3.  Задачи  на  движение:   

(в  системе  координат  время  t,  скорость  v)  описывается  уравнением  равносторонней  гиперболы. 

4.  Задачи  на  работу:  . 

5.  Задачи  на  нахождение  площади  прямоугольника:

(в  системе  координат  длина  а,  ширина  b  прямоугольника)  так  же  описываются  равносторонней  гиперболы.

6.  Общий  случай  дробно-линейной  функции:

который  легко  привести  к  виду:

преобразованием  параллельного  переноса: 

может  быть  сведен  к  равносторонней  гиперболе.

Список  литературы:

1.Ефимов  Н.В.  Краткий  курс  аналитической  геометрии.  Изд.  8.  «Наука»,  М.,  1965.

2.Погорелов  А.В.  Аналитическая  геометрия  Изд.  3.  «Наука»,  М.,  1968.

3.Штерман  И.Я.  Гиперболические  функции.  Гостехиздат,  М.  —  Л.  1935.