ЗАГАДОЧНОЕ ЧИСЛО ΠИ В КУРСЕ ШКОЛЬНОЙ ФИЗИКИ

Ловдин Владимир

класс 11 «Б», МБОУ «Средняя общеобразовательная школа № 10», г. Архангельск

Коптелов Геннадий Геннадьевич

научный руководитель, учитель математики первой квалификационной категории, МБОУ «Средняя общеобразовательная школа № 10» г. Архангельск

С уникальным числом, мы сталкиваемся постоянно, оно входит во множество формул в математике, физике, химии, биологии, даже в экономике. Это число абстрактно, но напрямую связано с окружающим миром. Основная наука о природе довольно часто использует это число для описания физических процессов, однако мало кто из учеников задумывался о его возникновении, Актуальность исследования определяется противоречием: с одной стороны, число π мы применяем часто и практически не задумываясь, с другой стороны, глубинный смысл мировой константы, маленького, но очень значимого числа остается для нас непознанным. Быть может, это число «скрывает» какие-то общие законы природы?

Цель исследования: выявить роль числа π в курсе школьной физики. Объект исследования: учебная литература по физике для 10—11 классов. Предмет исследования: число π в курсе школьной физики. Задачи: изучить историю появления числа π, проанализировать формулы физики, найти и оценить роль числа π в различных разделах физики.

Методы исследования: анализ учебной литературы по физике, классификация, обобщение, систематизация, математическое моделирование.

Работа состоит из введения, двух глав, заключения, списка литературы.

Во введении обосновывается актуальность исследования, цели, объект и предмет исследования, формулируются задачи, определяются основные методы исследования. В первой главе «Краткая история эволюции числа π» содержатся исторические сведения о числе π. Во второй главе «Роль мировой константы в курсе школьной физики» представлены обоснования применения числа π в различных разделах физики. В заключении сделаны выводы и определено практическое применение работы.

Краткая история эволюции числа π. Исторические факты свидетельствуют, что первым отношение длины окружности к ее диаметру обозначил современным символом английский математик У. Джонсон в 1706 г. Число пи он обозначил буквой греческого алфавита π (от слова "periferia" — окружность). В цифровом выражении π = 3,141592… и имеет бесконечное число цифр после запятой.

На протяжении многих столетий математики разных стран пытались выразить отношение длины окружности к диаметру рациональным числом. Древнеримский архитектор Витрувий в Трактате «Десять книг об архитектуре» свидетельствовал, что это число очень удобное приближение для строительной практики тех времён, так как, если измерить длину диаметра окружности, то затем легко получить отрезок, равный длине окружности [2, с. 17]. По расчётам Архимеда (287—212 лет до н. э.) отношение окружности к диаметру заключено между числами 310/71 и 31/7, а это означает, что π = 3,1419...

Цзу Чунчжи (429—500 гг.) — китайский учёный-математик впервые в мире рассчитал число π с точностью до седьмого знака после запятой. 3,1415927... Затем в первой половине XV века Джамшид ал-Каши, математик и астроном империи Улугбека, вычислил число π с 16 десятичными знаками, необходимое для составления таблицы синусов с шагом в 1' для применения в астрономии. В Европе французский математик Ф. Виет (1540—1603 гг.) заметил, что число π можно отыскать, используя пределы некоторых рядов. Это открытие позволило вычислять π с какой угодно точностью.

В начале XVII века голландский математик Лудольф ван Цейлен (1540—1610 гг.) нашёл 32 знака, потратив на это десятилетие своей жизни. Число π стали называть лудольфовым числом. Книгу, в которой он излагает эти вычисления, он заканчивает словами: «У кого есть охота, пусть пойдет дальше» [2, с. 31]. Вскоре после этого он сам потратил двенадцать лет и нашел еще пятнадцать десятичных знаков числа π.

Леонард Эйлер (1707—1783 гг.), впервые в 1736 г. воспользовался символом У. Джонсона и обозначение числа π стало общеупотребительным среди математиков. Эйлер вычислил его с точностью до 153 десятичных знаков. В 1794 году А.М Лежандр привёл доказательство иррациональности чисел π и 2π, а в 1882 году профессором Кёнигсбергского университета Линдеманом, была доказана трансцендентность числа π. [2, с. 50]

Поиски точного выражения числа π продолжались. С использованием электронных машин в 1949 г. получено значение числа π с 2035 знаками, а в 1963 г. было найдено уже 100265 десятичных знаков числа π. Последний рекорд, достигнутый на суперкомпьютерах — это 500 млрд. знаков.

Бертран Рассел (1872—1970 г.г.) английский математик, философ и общественный деятель, лауреат Нобелевской премии, писал: «Лицо p было скрыто маской…. Сквозь прорези маски пронзительно, безжалостно, холодно и загадочно смотрели глаза …» [2, с. 57]. Что же они могли увидеть?..

Недавно учёные под руководством доктора Чарльза Кэнтора расшифровали ДНК и там тоже не обошлось без числа π, то есть, оставаясь неизменным, оно держит под контролем многие физические процессы. По мнению ученых, определение всех знаков после запятой у числа p, позволит открыть множество тайн мироздания, часть из которых нам известна [1, c. 64].

Число π в основных законах школьной физики. Остановимся на применении числа в p физике. Мы живем в трехмерном пространстве. Наш мир чрезвычайно разнообразен и богат различными геометрическими фигурами. Известно, что сфера, круг, шар представляют собой идеально совершенные и сложные геометрические объекты, в то же время они выступают простейшими моделями многих физических явлений. Например, можно ли обойтись без числа π при описании механических явлений в кинематике?

Рассмотрим кинематику равномерного движения тела по окружности. Путь L, пройденный материальной точкой, равномерно движущейся по окружности за промежуток времени ∆t равен L=2πR (1), где L — длина окружности, R — радиус окружности.

Рисунок 1.

Тогда время одного полного оборота (период Т) равен:

Т=2 πR/V (2),

где: V — линейная скорость точки.

Из геометрии известно, что l = φR (3), где l — длина дуги, φ — угол поворота в радианах, R — радиус дуги. Разделим обе части уравнения (3) на t — время прохождения точки по дуге: l / t = φR/ t, l / t=V, φ/t = ω, где ω — угловая скорость, V — линейная скорость Таким образом, получили связь между линейной и угловой скоростью движения тела по окружности V=ωR (4). Подставляя (4) в уравнение (2) имеем: Т=2π/ω (5). Если ν — частота обращения (число оборотов в секунду), то с учетом обратно пропорционального соотношения между частотой и периодом имеем 1/ν =2π/ω, то есть ω=2πν. Тогда связь между линейной скоростью и частотой:

V = ωR = 2πνR [4, c. 44].

Вычисление центростремительного ускорения а_ц при равномерном движении по окружности также не обходится без числа π:

Подобным образом описывается вращение абсолютно твердого тела вокруг неподвижной оси, т. к. траекторией движения любой точки такого тела является окружность. Линейная скорость какой-либо точки абсолютно твердого тела пропорциональна расстоянию R точки от оси вращения, то есть:

V = ωR = 2πνR = 2πR/Т.

При равномерном вращательном движении углы поворота за равные промежутки времени одинаковы и мгновенная угловая скорость тела равна средней угловой скорости. Тангенциальные ускорения а_τ у различных точек абсолютно твердого тела отсутствуют а_τ = 0, а нормальное ускорение а_n какой–либо точки зависит от ее расстояния R до оси вращения и его вектор направлен в каждый момент времени по радиусу траектории точки к оси вращения:

а_n = V²/R = ω²R = 4π²ν²R

Таким образом, через число π определяется период, частота обращения материальной точки при равномерном движении тела по окружности, а также линейная и угловая скорости и центростремительное ускорение.

Число π в колебательных процессах. При колебаниях математический маятник движется по дуге окружности, т. е. величины, описывающие колебания, аналогичны тем, что описывают равномерное движение материальной точки по окружности. Для повторяющихся через определенные промежутки времени движений применяются такие физические величины как период Т, частота ν и циклическая частота ω. Траектория математического маятника представляет собой дугу, т. е. часть окружности. Тогда период колебаний Т связан с циклической частотой ω соотношением (5) Т = 2π/ω. Преобразуем это выражение, используя соотношение между угловой и линейной скоростью при движении тела по окружности.

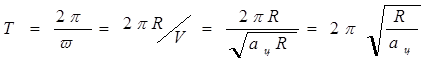
При малых углах φ центростремительное ускорение равно ускорению свободного падения, а радиус окружности R равен длине нити l математического маятника. Тогда Т = 2π и ω = .

Аналогично происходят колебания физического маятника и колебания в колебательном контуре. Для физического маятника Т = 2π, где m — масса маятника, k — жесткость пружины [4, c. 62].

Для колебательного контура Т = 2π, где С — электроемкость конденсатора, L — индуктивность катушки.

Число π используется при вычислении параметров гармонических колебаний, которые происходят по закону синуса или косинуса. Уравнение колебаний имеет вид:

х = Х₀ sin(2πt/T+φ_о),

где: X₀ — амплитуда колебаний,

t — время,

Т — период колебаний,

φ₀ — начальная фаза колебаний.

Рассмотрим раздел электростатики, в частности Закон Кулона для взаимодействия точечных зарядов q₁ и q₂ вакууме: F =  , где ε₀ = 8,8*10^-12 Ф/м — электрическая постоянная.

Выражение 4πR² есть не что иное, как площадь сферы. Аналогична формула напряженности электрического поля точечного заряда (шара радиуса r с зарядом q, равномерно распределенным по его поверхности), т. к. множество равноудаленных точек такого поля образуют сферу.

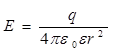
Понятно, что формула электроемкости уединенного шара будет обязательно включать число π, а именно: С = 4πε₀εR. После некоторых преобразований перейдем к формуле, которая по виду напоминает формулу для расчёта электроемкости плоского конденсатора с площадью пластин S и расстоянием между пластинами R:

В разделе электромагнетизм мы встречаемся с числом π при определении силы взаимодействия параллельных токов единичной длины

где: I₁ и I₂ — токи в параллельных проводниках единичной длины

μ — относительная магнитная проницаемость среды,

μ₀ = 4π*10^-7 Гн/м — магнитная постоянная. Это объясняется тем, что магнитные силовые линии замкнуты и представляют собой окружности.

Сила Лоренца F, действующая на заряженную частицу q, влетевшую в магнитное поле c индукцией В со скоростью V определяет движение частицы по окружности или по стирали и мы опять при решении задач встретимся с числом π.

При интерференции волн от двух когерентных источников максимум будет наблюдаться при фазовой разности хода волн ∆φ = πk, где k = 0,1,2,..

Далее мы встретились с числом π при расчетах мощности излучения ускоренно движущегося заряда: Р = μ₀q²А² ω⁴/12πс, где А — амплитуда колебаний заряда, μ₀ — магнитная постоянная, q — заряд, a — ускорение, с — скорость света; при расчёте средней мощности излучения диполя Герца, если к диполю подводится ток I = I₀sinωt, то Р = μ₀l² ω²I₀²/ 12πс [3, c. 70].

Таким образом, число π в физике не менее популярно, чем в математике. Оно возникает при оценке объёмов и площадей цилиндрических тел, его используют при расчёте плотности потока излучения от точечного источника или цилиндрического проводника, при оценке квантовых состояний атома. Без числа π не обойтись при расчете полного светового потока источника света, силы света, определении скорости света по методу Физо, изучении импульса фотона, волны де Бройля и во многих других случаях. Пи-мезоны (пионы) π⁺, π^-, π⁰ — выступают в роли переносчиков ядерного взаимодействия [5, c. 172].

Мы убедились, что переоценить значение этого загадочного и не имеющего точного значения числа π просто невозможно. Оно вездесуще, всепроникающее и бесконечно как Вселенная.

Предполагаем, что данный материал будет использоваться на элективных курсах предпрофильной и профильной подготовки старшеклассников, интересующихся физикой.

Список литературы:

1.Горобец Б. «Мировые константы в основных законах физики и физиологии»// Наука и жизнь № 2 — 2004 — с. 64—69

2.Жуков А.В. Вездесущее число «пи», — М.: Едиториал УРСС, 2004. — 216 с.

3.Касьянов В.А. Иллюстрированный атлас по физике: 11 класс / М.: Изд. «Экзамен», 2010. — 191 с.

4.Мякишев Г.Я. Буховцев Б.Б. Физика, 10 класс: учеб. для общеобразоват. учреждений, — М.: Просвещение, 2011 — 336 с.

5.Мякишев Г.Я. Буховцев Б.Б. Физика, 11 класс: учеб. для общеобразоват. учреждений, — М.: Просвещение, 2011 — 399 с.