ТАБЛИЧНАЯ ФУНКЦИЯ: ОПРЕДЕЛЕНИЕ, СВОЙСТВА, ПРИМЕНЕНИЕ

Нигматуллин Ильяс

класс 10 «А», АНО СОШ «Шанс», г. Кемерово

Шугалов Борис Семёнович

научный руководитель, канд. физ.-мат. наук, доцент КРИПКиПРО, г. Кемерово

Введение

Рассмотрим две числовые таблицы:

Т^* =  и Т =

таких, что одна из них получается из другой перестановками чисел в столбцах. Сопоставим каждой таблице число — значение таблицы f, равное сумме произведений чисел в строках:

f(T^*) = 2×1 + 5×4 = 22, f(T) = 2×4 + 5×1 = 13.

Значение таблицы Т^* оказалось больше значения таблицы Т. А можно ли предсказать этот результат, не проводя вычислений?

Таблица T^* характеризуется тем, что числа во всех её столбцах расположены в порядке возрастания. Рассмотрение других числовых примеров подтверждает предположение о том, что значение таблицы Т^*, у которой числа во всех столбцах расположены в порядке возрастания, не меньше значения таблицы, отличающейся от Т^* расположением чисел в столбцах.

Как доказать это свойство табличной функции?

Распространяется ли оно на таблицы большей размерности? Например, на таблицы, состоящих из двух строк и трёх столбцов?

Верно ли предположение о наибольшем значении табличной функции в общем случае, когда число строк в таблице равно m, а число столбцов — n?

В работе представлено доказательство теоремы о наибольшем значении табличной функции для таблиц произвольной размерности, m  n. Доказанная теорема является источником для получения ряда конкретных неравенств [3].

1.  Доказательство теоремы в простейшем случае.

Среднее арифметическое и среднее геометрическое двух чисел

Пусть Т^* =  , причём

Переставив числа во втором столбце таблицы Т^*, получим таблицу

Т = .

Покажем, что f(Т^*) ³ f(Т).

f(Т^*) = , f(Т) = .

f(Т^*) — f(Т) =  .

Отсюда следует f(Т^*) ³ f(Т), причём f(Т^*) = f(Т) тогда и только тогда, когда  или .

Переставив числа в первом столбце таблицы Т^*, получим таблицу:

Т₁ = , которая получается из Т перестановкой её строк. Но, очевидно, что при перестановке строк (и столбцов) таблицы её значение не изменяется: f(Т₁) = f(Т).

Переставив числа в обоих столбцах таблицы Т^*, получим таблицу, значение которой равно f(Т^*).

Итак, для любой таблицы Т^* =  , в которой , имеет место неравенство: f(Т^*) ³ f(Т), где Т — таблица, получающаяся из Т^* перестановкой чисел в столбцах.

Используя полученный результат, докажем, что среднее арифметическое двух неотрицательных чисел не меньше их среднего геометрического:  .

Имея в виду левую часть доказываемого неравенства, составим таблицу:

Т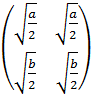^* =  ,  f(Т^*) =  .

Переставив числа во втором столбце таблицы Т^*, получим таблицу:

Т = 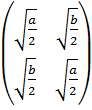 , f(Т) = .

По доказанному свойству таблицы Т^*, f(Т^*) ³ f(Т). Отсюда следует, что

. Отметим, что равенство имеет место в том и только в том случае, когда a = b.

2.  Доказательство теоремы для двухстрочных таблиц

Распространяется ли доказанное свойство на таблицы большей размерности? Представим числовой пример, дающий отрицательный ответ на поставленный вопрос.

Т^* =  , f(Т^*) = 14, Т =  , f(Т) = 19, f(Т^*) < f(Т).

В построенном контрпримере элементы таблицы являются положительными и отрицательными числами. При дальнейшем рассмотрении будем считать, что элементы таблицы неотрицательные числа. Докажем теорему для случая, когда размерность таблицы 2n.

Пусть в таблице

Т^* =

числа в столбцах расположены в порядке возрастания:

 ,  , …,.

Без ограничения общности можно считать, что другая таблица Т получается из Т^* перестановкой чисел в первых k — 1 столбцах:

Т = .

Для упрощения записи введём обозначения:

, ,

, .

Как и при доказательстве простейшего случая, раскроем разность

f(Т^*) — f(Т) =  =

.

Так как, по условию,  ,  , …,, то по правилу умножения неравенств [1, С. 30; 2, С. 26],

, т. е. множитель  неотрицателен. Аналогично устанавливается неотрицательность второго множителя, . Таким образом, f(Т^*) — f(Т)  0 или f(Т^*) ³ f(Т). Теорема о наибольшем значении табличной функции для двухстрочных таблиц доказана.

3.  Доказательство теоремы о наибольшем значении табличной функции (общий случай)

Используя метод математической индукции [1, С. 16], докажем теорему в общем случае.

Для таблиц размерности 2n теорема доказана.

Допустим, что теорема справедлива для таблиц размерности (m -1)n. Докажем, что она справедлива и для таблиц размерности mn.

Пусть Т — любая таблица размерности mn, элементы которой неотрицательные числа. По таблице Т строим таблицу Т₁, у которой первая строка совпадает с первой строкой таблицы Т, а остальные числа в каждом столбце таблицы Т₁ — это расположенные в порядке возрастания числа соответствующего столбца таблицы Т.

 ®  ®  ®

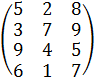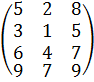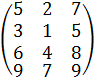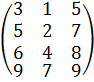
Т                      Т₁                               Т₂                     Т₃

Пример построения последовательности таблиц по данной таблице Т.

Обозначим через Т^¢ (и ) таблицу размерности (m -1)n, получающуюся из Т (соответственно из Т₁) удалением первой строки. Тогда

f(Т) = a + f(Т^¢), f(Т₁) = a + f(),

где: а — произведение чисел первой строки таблицы Т.

Так как, по предположению индукции, f(Т^¢)  f(), то и f(Т)  f().

Далее, по таблице Т₁ строим таблицу Т₂, у которой вторая строка совпадает со второй строкой таблицы Т₁, а остальные числа в столбцах расположены в порядке возрастания. Как и на предыдущем шаге, получаем неравенство: f(Т₁)  f().

Наконец, по таблице Т₂ строим таблицу Т₃, у которой третья строка совпадает с третьей строкой таблицы Т₂, а остальные числа в столбцах расположены в порядке возрастания. При этом, имеет место неравенство: f(Т₂)  f().

Сводный результат, связывающий между собой значения таблиц Т, Т₁, Т₂ и Т₃, представляет собой цепочку неравенств: f(Т)  f() f() f().

Заметим, что построение последовательности различающихся таблиц Т, Т₁,… обрывается на третьем шаге, так как Т₃ = Т^*.

Таким образом, для любой таблицы Т, которая получается из Т^* перестановками чисел в столбцах имеет место неравенство: f(Т)  f(Т^*). Теорема доказана.

В разделе 1 доказана теорема о среднем арифметическом и среднем геометрическом для двух неотрицательных чисел. Аналогично, используя теорему о наибольшем значении табличной функции, нетрудно доказать, что среднее арифметическое п чисел не меньше их среднего геометрического.

Список литературы:

1. Алгебра и начала анализа: учеб. для 10 кл. общеобразоват. учреждений: базовый и профил. уровни / [С.Н. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин]. — М.: Просвещение, 2009.

2.  Беккенбах Э. Введение в неравенства / Э. Беккенбах, Р. Беллман. — М.: Мир, 1965.

3. Шугалов Б.С. Постановка и решение исследовательских задач в классах физико-математического профиля: учебно-методическое пособие / Б.С. Шугалов. — Кемерово: Изд-во КРИПКиПРО, 2007.