ЭКСПОНЕНЦИАЛЬНАЯ ЗАВИСИМОСТЬ В ПРИРОДНЫХ ПРОЦЕССАХ

Стойков Дмитрий

10 «А» класс МБОУ СОШ № 177,г. Казань

Хабибуллина Альфия Якубовна

научный руководитель, учитель математики высшей категории МБОУ СОШ № 177,г. Казань

 

Введение

В природе и жизни человека встречается большое количество процессов, в которых некоторые величины изменяются так, что отношение данной величины через равные промежутки времени не зависит от времени. Среди таковых можно назвать радиоактивный распад веществ, рост суммы на счету в банке и др. Все эти процессы описываются показательной функцией. Меня заинтересовал вопрос, почему протекание этих процессов не зависит от времени. Ведь по логике, любые изменяющиеся процессы должны соотноситься с независимой величиной ― временем. На деле же, это правило работает не всегда.

Цель исследовательской работы: экспериментально подтвердить протекание некоторых химических процессов в соответствии с экспоненциальной зависимостью, описываемой уравнением Аррениуса.

Задачи:

·Изучить показательную функцию;

·Изучить экспоненциальную зависимость, как частный случай показательной функции;

·Изучить уравнение Аррениуса, описывающее экспоненциальную зависимость;

·Изучить примеры химических процессов, протекающих в соответствии с экспоненциальной зависимостью;

·Провести ряд экспериментов и подтвердить на практике протекание некоторых химических процессов в соответствии с экспоненциальной зависимостью, описываемой уравнением Аррениуса.

Гипотеза исследования: при помощи уравнения Аррениуса можно описать некоторые химические процессы.

Объект исследования: показательная функция, как элемент прикладной математики.

Методы исследования:

1.  Изучение литературы и электронных ресурсов по теме исследования.

2.  Анализ применения экспоненциальной зависимости

3.  Химические эксперименты на подтверждение уравнения Аррениуса.

Показательная функция

Пусть х  R, a ≠ 0, {r_n} ― последовательность рациональных чисел, сходящихся к x. Определим число a^x как предел. Показательной функцией с основанием a > 0, а ≠ 1 называется функция вида у=a^x, х  R

Данный предел не зависит от выбора последовательности r_n, приводящей к числу x. Областью определения показательной функции является вся числовая ось. Эта функция непрерывна, монотонно возрастает при a > 1  и монотонно убывает при 0 < a < 1 . Функция никогда не обращается в ноль, но имеет горизонтальную асимптоту y = 0.

График показательной функции у=0,5^х

Экспоненциальная зависимость

 

Особое значение в приложениях имеет показательная функция, в качестве основания которой используют число e, определяемое как

Численно оно равно е = 2,71828182845904523536 и называется константой 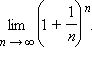Эйлера.

Определенная так функция называется экспоненциальной или просто экспонентой и обозначается у = е^х ≡ exp x.

 

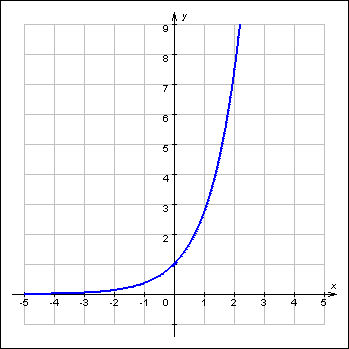
Рассмотрим график экспоненциальной функции y = e^x. Так как 2 < е < 3, то функция у = е^х монотонно возрастающая на всей области определения. В точке (0;1) касательная наклонена к оси абсцисс под углом 45^о (π/4). Производная этой функции в нуле равна 1. Это ― единственная функция, у которой производная и первообразная совпадают с нею же самой.

 

 

 

 

 

 

 

 

Уравнение Аррениуса

Шведский физик и химик Сванте Аррениус получил Нобелевскую премию по химии в 1903 г. за создание теории электролитической диссоциации. В своей докторской диссертации (Уппсальский университет) Аррениус высказал предположение, что такие «молекулы», как хлорид натрия, самопроизвольно распадаются в растворе, образуя ионы, которые исполняют роль реагентов при электролизе. Однако более всего Аррениус известен своим уравнением, определяющим температурную зависимость константы скорости реакции.

Точное соотношение между скоростью реакций и температурой Аррениус впервые установил в 1889 г. Это соотношение, получившее название уравнения Аррениуса, имеет вид

,

где:      к ― константа скорости реакции;

А ― постоянная, характеризующая каждую конкретную реакцию (константа Аррениуса);

e ― экспонента;

E_a ― еще одна постоянная, характерная для каждой реакции и называемая энергией активации;

R ― газовая постоянная;

Т ― абсолютная температура в градусах Кельвина.

Отметим, что это уравнение связывает температуру не со скоростью реакции, а с константой скорости.

Связь скорости реакции с температурой была выведена из результатов первых кинетических исследований в 1880―1884 гг. и получила название правила Вант-Гоффа: скорость многих реакций при нагревании на 10^оС увеличивается в 2―4 раза. Данное правило выполняется для относительно медленных реакций в растворах и поэтому не является универсальным. При решении некоторых задач можно пользоваться формулой Вант-Гоффа:

где: γ ― коэффициент Вант-Гоффа ( = 2―4),

Т ― температура в градусах по шкале Цельсия или Кельвина (поскольку используется разность, шкала не имеет значения).

Уравнением Аррениуса более точно и более универсально выражает зависимость константы скорости реакции от температуры. Множитель А в этом уравнении связан с частотой столкновений частиц и их ориентацией при столкновениях.

Примеры природных процессов, протекающих в соответствии с уравнением Аррениуса

Пример 1. Скорость (частота) пиликанья сверчков подчиняется, хотя и не вполне строго, уравнению Аррениуса, плавно увеличиваясь в температурном интервале от 14.2°С до 27°С, с эффективной энергией активации E_a = 51 кДж/моль. По частоте стрекотаний можно достаточно точно определить температуру: надо подсчитать их число за 15 с и прибавить 40, получится температура в градусах Фаренгейта (F) (американцы до сих пор пользуются этой температурной шкалой). Так, при 55 F (12.8°С) частота стрекотаний составляет 1 стрек./с, а при 100 F (37.8°С) ― 4 стрек./с.

 

 

Пример 2. В температурном интервале от 18°С до 34°С частота сердечных сокращений морской черепахи согласуется с уравнением Аррениуса, которое дает энергию активации E_a = 76.6 кДж/моль, но при более низких температурах энергия активации резко увеличивается. Это может быть связано с тем, что при пониженных температурах черепаха чувствует себя не очень хорошо и частота ее сердечных сокращений начинает управляться другими биохимическими реакциями.

Пример 3. Особенно интересны попытки «положить на аррениусовскую зависимость» психологические процессы человека. Так, людей с разной температурой тела (от 36.4°С до 39°С) просили отсчитать секунды. Оказалось, что чем выше была температура, тем быстрее был счет (Е_а = 100.4 кДж/моль). Таким образом, наше субъективное ощущение времени подчиняется уравнению Аррениуса. Автор проведенного социологического исследования Г. Хогланд предположил, что это связано с некоторыми биохимическими процессами в мозге человека.

Немецкий исследователь Х. фон Ферстлер измерял у людей с разной температурой скорость забывания. Он давал людям последовательность разных знаков и измерял время, в течение которого люди эту последовательность помнили. Результат был тот же, что и у Хогланда: аррениусовская зависимость с Е_а = 100.4 кДж/моль.

Богатый народный опыт подсказывает многие выводы, которые подтверждаются научно. На Руси издавна существует поговорка: «Держи ноги в тепле, а голову ― в холоде». Уравнение Аррениуса обосновывает это высказывание.

 

 

Зависимость скорости химических реакций от температуры

Изменение температуры оказывает резкое влияние на константу скорости, а, следовательно, и на скорость химической реакции. В подавляющем большинстве случаев скорость химической реакции с нагреванием возрастает.

В соответствии с правилом Вант-Гоффа, при повышении температуры на каждые 10 градусов скорость химической реакции возрастает, в среднем, в 2—4 раза:

v₂ = v₁×γ^(T2-T1)/10,

где: γ - температурный коэффициент, который можно рассчитать по формуле:

γ = k_T+10/k_T,

где: k_T — константа скорости реакции при температуре Т;

k_T+10 — константа скорости реакции при температуре (Т+10).

Эксперименты

Эксперимент № 1: Взаимодействие цинка с разбавленной серной кислотой.

Взяли несколько кусочков цинка с точно известной массой и поместили в равные объемы растворов разбавленной серной кислоты различной температуры. Измерили время полного растворения цинка, проходящего в соответствии с реакцией:

Zn + H₂SO₄ = ZnSO₄ + H₂↑

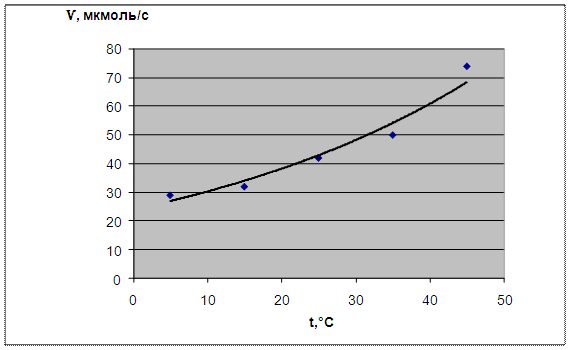
Рассчитали скорость реакции в мкмоль/с (количество вещества в моль посчитано через массу, деленную на атомную массу цинка). Результаты представлены в таблице и в виде графика зависимости скорости реакции от температуры.

Таблица 1.

Зависимость скорости взаимодействия цинка с разбавленной серной кислотой от температуры серной кислоты: 

 

Эксперимент № 2: Влияние температуры на скорость ферментативной реакции.

В качестве модельной ферментативной реакции мы взяли реакцию гидролиза бутирилхолина, катализируемую ферментом бутирилхолинэстеразой:

(СН₃)₃N⁺-CH₂-CH₂-O-C(O)-C₃H₇ + H₂O → (СН₃)₃N-CH₂-CH₂-OH + HO-C(O)-C₃H₇

Трехмерная модель молекулы бутирилхолинэстеразы.

 

Для проведения реакции использовали планшет для иммунохимических исследований (см. рисунок 1 Приложения 1). Приготовили растворы субстрата ― бутирилхолина и фермента ― бутирилхолинэстеразы путем растворения точной навески вещества в 0.002 моль/л фосфатном буферном растворе, содержащем кислотно-основной индикатор бромтимоловый синий, с pH = 8. Индикатор имеет синюю окраску в щелочной среде (рН>7) и желтую окраску в кислой среде. Так как в результате ферментативной реакции гидролиза происходит образование кислоты, рН раствора понижается, а окраска индикатора изменяется от синей через зеленую до желтой. Таким образом, скорость химической реакции можно оценить по скорости изменения окраски индикатора.

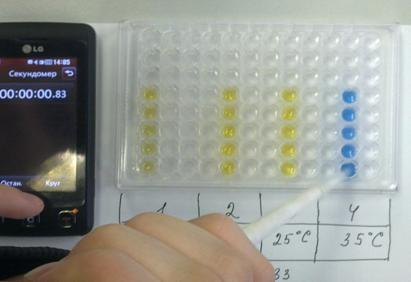
Проведение реакции. Растворы субстрата и фермента с помощью снега и водяной бани охлаждали либо нагревали до нужной температуры (5°С, 15°С, 25°С, 35°С). Максимальной температурой было выбрана температура 35°С, т. к. фермент холинэстераза имеет температурный оптимум 37°С (температура, при которой активность фермента максимальна). В ячейку планшета с помощью дозатора на 100 мкл вносили раствор фермента определенной температуры, затем 100 мкл раствора субстрата и засекали время с помощью секундомера. Измеряли время от начала реакции (момент добавления субстрата к ферменту) до изменения цвета индикатора до желтого. При каждой температуре эксперимент проводили в трех повторностях, затем рассчитывали среднее время изменения окраски.

 

Зависимость времени изменения окраски индикатора от температуры растворов:

 

 

 

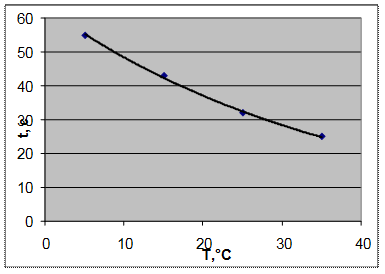
Данный метод оценки скорости реакции является вариантом каталитического метода анализа — способом фиксированной концентрации. Это способ, в котором реакцию проводят до строго определенной (фиксированной) концентрации индикаторного вещества и измеряют время достижения этой концентрации. В данной реакции индикаторным веществом является масляная кислота, от концентрации которой зависит окраска индикатора. Время достижения определенной концентрации является мерой скорости реакции. График строят в координатах: величина, обратная времени достижения фиксированной концентрации — изучаемый параметр (температура).

 

 

 

 

Зависимость скорости изменения окраски индикатора от температуры:

 

 

Эксперимент № 3 (расчетная задача): Скорость дегидратации этилового спирта.

Задача: Во сколько раз увеличится скорость дегидратации этилового спирта при увеличении температуры со 180^оС до 200^оС, если температурный коэффициент реакции равен трем?

Решение: В соответствии с правилом Вант-Гоффа, v₂ = v₁×γ^(T2-T1)/10, отсюда

v₂/v₁ = γ^(T2-T1)/10 , где γ = 3, Т1 = 180, Т2 = 200. Таким образом, v₂/v₁ = 3^(200-180)/10 = 9, т. е. скорость возрастет в 9 раз при повышении температуры на 20 градусов.

По полученным данным можно построить графическую зависимость скорости дегидратации этилового спирта от температуры (при повышении температуры на каждые 10 градусов скорость реакции возрастает в 3 раза).

Зависимость скорости реакции от температуры: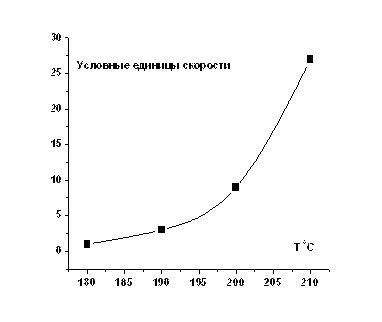

 

Выводы. Заключение

В процессе работы над исследовательской темой была изучена показательная функция, экспоненциальная зависимость, как частный случай показательной функции, а также уравнение Аррениуса, описывающее экспоненциальную зависимость.

После рассмотрения примеров природных процессов, протекающих в соответствии с экспоненциальной зависимостью, был проведен ряд химических экспериментов и подтверждено на практике протекание некоторых химических процессов в соответствии с экспоненциальной зависимостью, описанной уравнением Аррениуса.

Мы считаем, что гипотеза исследования «при помощи уравнения Аррениуса можно описать некоторые химические процессы» подтвердилась. Так, при растворении Zn в серной кислоте при разных температурах скорость протекания химической реакции изменяется по экспоненте. Кроме того, скорость ферментативной реакции в нейронах человеческого мозга также изменяется в зависимости от температуры в соответствии с уравнением Аррениуса.

 

Таким образом, было экспериментально подтверждено протекание некоторых химических процессов в соответствии с уравнением Аррениуса, описываемым экспоненциальной зависимостью.

 

Список литературы:

1.Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. М.: Наука, 1987. — 688 с.

2.Леенсон И.А. Почему устарело правило. Энциклопедия для детей. Т. 17. Химия. — М.: Аванта+, 2000. — 640 с.

3.Леенсон И.А. Почему и как идут химические реакции. — М.: МИРОС, 1994. — 176 с.

4.Хапланов М.Г. Теория функции комплексного переменного (краткий курс). М.: Просвещение, 1965. — 209 с.