Статья опубликована в рамках: II Международной научно-практической конференции ««Проба пера» ЕСТЕСТВЕННЫЕ И МАТЕМАТИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 29 ноября 2012 г.)
Наука: Математика
Секция: Алгебра
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МАТЕМАТИЧЕСКАЯ ГАРМОНИЯ ЦВЕТИКА-СЕМИЦВЕТИКА
Курицына Юлия
класс 7 «Г», школа № 177, г. Казань
Хабибуллина Альфия Якубовна
научный руководитель, учитель математики высшей категории, школа № 177, г. Казань
Юрлина Дария Робертовна
научный руководитель, учитель математики, школа № 177, г. Казань
Введение
В 6 классе мы изучали темы «Поворот» и «Центральная симметрия». Я начала присматриваться к деревьям, кустарникам, к комнатным цветам и заметила очень интересную закономерность: если цветок симметричен, то он особенно красив. Я поняла, что красота природы зависит, в том числе, и от того, обладают ли окружающие нас растения симметрией.
Тема моего исследования: Математическая гармония Цветика–семицветика
Цель исследования: проведя систематизацию видов симметрии, на фотоохоте обнаружить представителей флоры, обладающих всеми видами симметрии, а также научиться строить правильные многоугольники.
В связи с поставленной целью определились следующие задачи:
1.Изучить известные материалы (книги, электронные источники и др.) по теме исследования. Ознакомиться с историей изучения симметрии.
2.Рассмотреть виды симметрии и другие виды движения на плоскости
3.Сходить на фотоохоту за симметрией растений и научиться строить правильные многоугольники
Гипотеза: существуют растения, обладающие всеми видами симметрии и другими видами движения на плоскости, можно построить «семицветик»
Методы исследования:
1. Изучение научно-популярной литературы по теме исследования
2. Систематизация полученных знаний
3. Классификация видов симметрии и других видов движения на плоскости
4. Классификация фотоснимков представителей флоры
I. Классификация видов движения фигур на плоскости
Движением фигур на плоскости называется преобразование фигур, при котором расстояние между любыми двумя точками сохраняется. Движение сохраняет форму и размеры любой геометрической фигуры.
В геометрии рассматриваются следующие виды движения на плоскости: осевая симметрия, центральная симметрия, поворот и параллельный перенос.
Осевая симметрия.
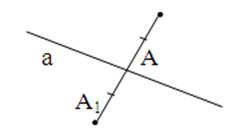
Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией.
Центральная симметрия.
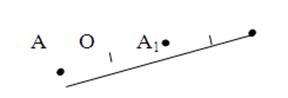
Две точки А и А1 называются симметричными относительно точки О, если О — середина отрезка АА1 .
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.
Поворот.
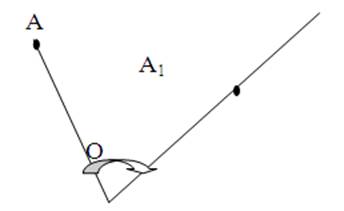
Поворотом на плоскости точки А в точку А1 называется такое движение, при котором каждый луч, исходящий из центра О, поворачивается на один и тот же угол в одном и том же направлении.
Параллельный перенос
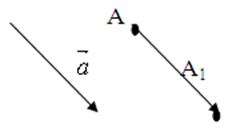
Параллельным переносом на вектор ![]() называется отображение плоскости на себя, при котором каждая точка А отображается в точку А1 так, что
называется отображение плоскости на себя, при котором каждая точка А отображается в точку А1 так, что ![]() =
= ![]() .
.
II. Из истории изучения симметрии
Симметрия является фундаментальным свойством природы, представление о котором, как отмечал академик В.И. Вернадский (1863—1945), «слагалось в течение десятков, сотен, тысяч поколений». «Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло ее в рисунке и в предметах быта. Надо полагать, что применение симметрии в первобытном производстве определялось не только эстетическими мотивами, но в известной мери и уверенностью человека в большей пригодности для практики правильных форм». Это слова другого нашего замечательного соотечественника, посвятившего изучению симметрии всю свою долгую жизнь, академика А.В. Шубникова (1887—1970). Первоначальное понятие о геометрической симметрии как о гармонии пропорций, как о «соразмерности», что и означает в переводе с греческого слово «симметрия», с течением времени приобрело универсальный характер и было осознано как всеобщая идея инвариантности (т. е. неизменности) относительно некоторых преобразований.
Таким образом, геометрический объект или физическое явление считаются симметричными, если с ними можно сделать что-то такое, после чего они останутся неизменными. Например, пятиконечная звезда, будучи повернута на 72° (360° : 5), займет первоначальное положение, а ваш будильник одинаково звенит в любом углу комнаты. Первый пример дает понятие об одном из видов геометрической симметрии — повороте, а второй иллюстрирует важную физическую симметрию — однородность и изотропность (равнозначность всех направлений) пространства. Легко вообразить, какая бы царила на Земле неразбериха, если бы эта симметрия была нарушена!
Таким образом, не только симметричные формы окружают нас повсюду, но и сами многообразные физические и биологические законы гравитации, электричества и магнетизма, ядерных взаимодействий, наследственности пронизаны общим для всех них принципом симметрии. «Новым в науке явилось не выявление принципа симметрии, а выявление его всеобщности»,— писал Вернадский. Действительно, еще Платон мыслил атомы четырех стихий — земли, воды, огня и воздуха — геометрически симметричными в виде правильных многогранников. И хотя сегодня «атомная физика» Платона кажется наивной, принцип симметрии и через два тысячелетия остается основополагающим принципом современной физики атома. За это время наука прошла путь от осознания симметрии геометрических тел к пониманию симметрии физических явлений.
Если фигура обладает осевой симметрией, то такая фигура состоит как бы из двух половинок, одна из которых является зеркальным отражением другой.
Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая их орнаментами, размечая территории на поверхности земли, измеряя расстояния и площади земельных участков, человек применял свои знания о форме, размерах и взаимном расположении предметов, использовал свои геометрически знания, полученные из наблюдений и опытов.
Рассмотрим варианты симметрии на примере пар лепестков:
a. — совместимо равные;
b. — зеркально равные;
c. — и совместимо и зеркально равные. Фигуры из пяти лепестков:
d. — расположенных относительно друг друга хаотично;
e. — закономерно.
III. Фотоохота.
В ходе исследования я начала фотографировать комнатные растении наших школьных кабинетов сначала на телефон. А потом, взяв фотоаппарат, мы с научным руководителем направились в школьную оранжерею, где я постаралась найти растения, обладающие каким-нибудь видом движения.
Во время просмотра отснятых фотографий, я заметила, что большинство растений имеет различные виды симметрии. Я отобрала изображения, которые имеют только осевую симметрию и увидела, что нет растений только с центральной симметрией, или только с поворотом. Я отобрала группу с осевой симметрией и поворотом, но у меня не получилось создать группу только с поворотом и центральной симметрией, или только с осевой и центральной симметрией. Однако, я увидела группу растений, которые обладают всеми видами симметрии, и задумалась, почему это так? Именно поэтому в разделе «Исследование углов поворота» я рассмотрела формы растений и постаралась выявить признаки, по которым можно классифицировать те или иные группы. Таким образом, я выделила 3 группы растений:
1. Растения, обладающие только осевой симметрией

2. Растения, обладающие осевой симметрией и поворотом.

3. Растения, обладающие всеми видами движения на плоскости.

Все фотографии сделаны в оранжерее школы № 177 г. Казани
IV. Исследование углов поворота
При изучении фотоснимков некоторые цветы мне показались более гармоничными, чем другие. Причем именно они по форме напоминали известные нам геометрические фигуры: равносторонний треугольник, квадрат, шестиугольник с равными сторонами. Все эти фигуры являются правильными многоугольниками. Чем точнее эти растения вписывались в многоугольник, тем красивее и гармоничнее они выглядели.

Хотя на уроках математики многоугольники мы ещё не проходили, я попыталась построить правильные многоугольники. Я долго пыталась это сделать при помощи линейки и карандаша. Но у меня почему-то это плохо получалось. И тут я вспомнила, как мой старший брат строил циркулем на чертежах окружности. И меня осенило: а не попробовать ли мне поработать с циркулем? Построив циркулем окружность, тем же раствором циркуля я сделала 6 насечек на окружности. И, о чудо! 6 хорд окружности оказались сторонами правильного шестиугольника. Если эти насечки соединить не подряд, а через одну, то получим правильный треугольник.
А как же построить с помощью циркуля квадрат? В окружности проведем два перпендикулярных диаметра АВ и КР. Вершины АРКВ образуют квадрат.
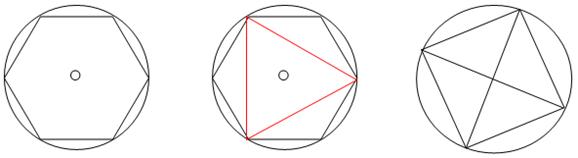
Интереснее вопрос, как построить любой правильный n-угольник?
Построение:
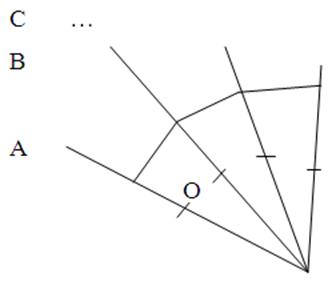
1. Берем точку О на плоскости (на листе бумаги). Проводим луч ОА.
2. В n-угольнике n сторон, n углов. Значит, 360º:n градусная мера откладываемых углов от точки О.
3. От луча ОА отложим угол АОВ в 360 : n градусов.
4. От луча ОВ таким же образом отложим угол ВОС, равный углу АОВ, и т. д. Таким образом, мы должны построить n углов.
5. На сторонах данных углов от точки О откладываем равные отрезки.
6. Соединив полученные точки на сторонах углов, получим правильный n-угольник.
Заметим, что центральная симметрия есть только у тех растений, у которых четное число лепестков. То есть, если рассматривать многоугольники, то центральная симметрия есть у многоугольников с четным числом сторон.
V. «Цветик-семицветик»
А как же быть, если нечетное число сторон у многоугольника? Вспомним известную сказку В. Катаева «Цветик-семицветик». У цветка с семью лепестками есть движения: осевая симметрия, поворот, но нет центральной симметрии. И как построить правильный семиугольник? Воспользуемся найденным способом с использованием формулы и транспортира. ![]()
Последовательно откладываем от точки О лучи ОА, ОВ, ОС, OD, OE, OF, OG, образующие углы по ![]() . На лучах откладываем равные отрезки от точки О. Последовательно соединяем концы отрезков и получаем семиугольник ABCDEFG.
. На лучах откладываем равные отрезки от точки О. Последовательно соединяем концы отрезков и получаем семиугольник ABCDEFG.



К сожалению, в моей фотоохоте не было «трофея» с семью лепестками, но мне все же удалось найти фотографию «семицветика» в интернет-ресурсах.

Выводы и заключение
В ходе исследования мне довелось изучить известные материалы (книги, электронные источники и др.) по теме исследования, ознакомиться с историей изучения симметрии, рассмотреть виды симметрии и другие виды движения на плоскости, сходить на фотоохоту за симметрией растений.
В начале исследования была выдвинута гипотеза: существуют растения, обладающие всеми видами симметрии и другими видами движения на плоскости? Сейчас я точно знаю, что существуют растения, обладающие всеми видами симметрии и другими видами движения на плоскости: и осевой симметрией, и центральной симметрией, и поворотом.
Я не только обнаружила представителей флоры, обладающих симметрией, но и выяснила, как научиться строить правильные многоугольники, обладающие этими же свойствами. Кроме того, предложенный мною метод построения правильного n-угольника с помощью транспортира, позволяет выполнять построения при n≥3. Я также смогла построить правильный семиугольник по мотивам сказки В. Катаева «Цветик-семицветик»
Мне эта тема очень понравилась. Наблюдая за растениями, я увидела не только красоту окружающей нас природы, но и поняла, что математика — не сухая наука, а неотъемлемая часть жизни.
Список литературы:
1. Атанасян Л.С., Геометрия 7—9, М. — Просвещение, 2011, — с. 384
2. Тарасов Л.В. Этот удивительно симметричный мир. М., Просвещение, 1996, — с. 180.
3. Урманцев Ю.А. Симметрия в природе и природа симметрии. М., Мысль, 1974, — с. 230.
4. [Электронный ресурс] ― Режим доступа. — URL: http://otherreferats.allbest.ru/biology/00125293_0.html
5. [Электронный ресурс] ― Режим доступа. — URL: http://www.refu.ru/refs/19/3283/1.html
дипломов

Оставить комментарий