ПОВЕРХНОСТНЫЙ  ИНТЕРПОЛЯЦИОННЫЙ  МЕТОД  НА  ОСНОВЕ  ПРИНЦИПА  НАИМЕНЬШИХ  КВАДРАТОВ

Данг  Нгок  Хоанг  Тхань

аспирант  Тульского  государственного  университет,  РФ,  г.  Тула

Email :  myhoangthanh@yahoo.com

Фан  Зуй  Тунг

магистрант  Тульского  государственного  университет,  РФ,  г.  Тула

Email: 

A  SURFACE  INTERPOLATION  METHOD  BASED  ON  LEAST  SQUARE  PRINCIPLE

Dang  Ngoc  Hoang  Thanh

postgraduate  student  of  Tula  State  University,  Russia,  Tula

Phan  Duy  Tung

graduate  student  of  Tula  State  University,  Russia,  Tula

АННОТАЦИЯ

В  работе  приведён  метод  для  построения  поверхностной  интерполяционной  функции  для  аппроксимации  заданных  данных.  Предлагаемый  метод  основан  на  принципе  наименьших  квадратов. 

ABSTRACT

In  this  paper  we  introduce  a  surface  interpolation  method  to  approximate  given  data.  This  method  based  on  least  square  principle. 

Ключевые  слова:   Принцип  (метод)  наименьших  квадратов;  поверхностный  интерполяционный  метод;  трёхмерный  компьютерный  график. 

Keywords:   Least  square  principle;  surface  interpolation;  3D  graphics. 

Задача  реконструкции  поверхностей  объектов  является  важной  задачей  в  компьютерном  графике  и  имеет  широкие  приложения  в  других  научно-технических  сферах.  Особенно  в  археологии,  обнаруженные  детали  всегда  содержат  дефекты  поэтому  нужна  реконструкция  их  поверхностей.  Такая  задача  широко  изучена  многими  ученными,  о  которых  говорится  в  [11,  8,  14,  2].  Однако,  целью  этой  работы  является  реконструкция  поверхности  методом  построения  аналитической  функции.  Рассматриваемая  задача  более  простая,  чем  вышеуказанная  задача. 

По  принципу,  для  построения  интерполяционной  функции,  надо  определить  связь  между  переменными  с  помощью  заданных  данных.  Пусть  в  Декартовой  системе  координата,  заданы  наборы 

где:  —  натуральное  число. 

Надо  найти  функцию  двух  переменных    

и  такую,  что

Для  нахождения  такой  функции,  используется  подход  наименьших  квадратов  [14,  2,  16,  6].  Наборы  данных    определяются  с  помощью  измерительных  приборов.  Пусть  наборы  данных  выполняют  какое-то  правило,  например,  где  называется  законом  распределения  данных. 

Функция    может  быть  определена  с  помощью  интерполяции  бикубического  сплайна  [5,  7,  15,  13].  Интерполяция  бикубического  сплайна  имеет  высокую  точность,  но  её  скорость  выполнения  недостаточно  быстрая.  Главной  идеей  работы  является  построение  поверхностной  интерполяционной  функции  на  основе  принципа  наименьших  квадратов,  у  которой  отклонение  с  начальными  данными  выполняет  следующий  критерий:

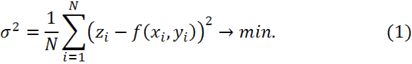
Принцип  наименьших  квадратов  применяется  для  решения  граничных  задач,  обработки  данных  в  статистике  и  т.  д.  Данный  метод  имеет  высокую  точность  и  высокую  скорость  вычисления.  В  этой  работе  построим  поверхностный  интерполяционный  метод  в  трёхмерном  пространстве  на  его  основе.

Поверхностный  интерполяционный  метод 

Пусть  заданы  наборы  данных.  Для  построения  поверхностной  интерполяционной  функции,  надо  выбрать  базис  функций.  Предлагается  два  следующего  базиса  функций:

(1)  Полиномиальный  базис  функций  и  пробуемая  функция

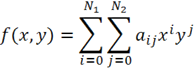
(2)  Тригонометрический  базис  функций  и  пробуемая  функция

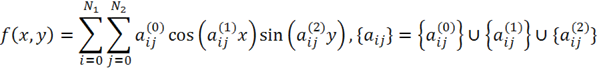
где  —  натуральные  числа.  В  функции  содержатся  параметры.  Без  ограничения  общности,  запишем.  Согласно  критерию  (1),  построим  следующий  функционал  энергии:

Надо  найти  параметры  для  того  чтобы  функционал  достигла  минимума.  Один  из  известных  методов  —  метод  градиента  спуска.  Основой  данного  метода  является  нахождение  стационарных  точек.  Стационарные  точки  определяются  с  помощью  решении  следующей  системы  уравнений:

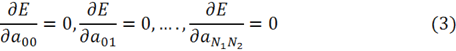
Существует  много  методов  для  решения  системы  уравнений  (3).  Одним  из  эффективных  методов  является  метод  Ньютона  [1].  С  помощью  рассмотрения  знаков  частных  производных  2-ого  порядка  на  стационарных  точках,  можем  определить  с  какими  значениями  параметров  функционал  энергии  достигает  минимума.  Используя  метод  градиента  спуска,  существуют  достоинства: 

·     Для  пробуемых  функций  более  2-ух  параметров,  трудно  определить  какие  стационарные  точки  являются  минимумом.

·     Итерационные  методы  (включая  метод  Ньютона)  могут  не  сходиться.

В  вычислительной  математике,  существует  несколько  методов,  которые  позволяют  найти  минимум  функционала  энергии  как  метод  Нелдера-Мида  [3,  4,  9,  10,  12].  Такой  метод  эффективен  для  решения  задачи  безусловной  оптимизации  функций  с  большим  количеством  переменных.  Метод  Нелдера-Мида  состоит  из  двух  этапов:

Начальный  этап .  Выбрать  точки  образующие  симплекс,  коэффициент  растяжения,  коэффициент  сжатия  и  коэффициент  отражения.  Перейти  к  основному  этапу.

Основной  этап .

Шаг  1 .  Положить  такими,  что

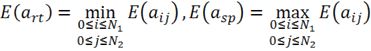
Положить  и  перейти  к  шагу  2.

Шаг  2 .  Положить.  Если,  то  положить    и  перейти  к  шагу  3.  В  противном  случае  перейти  к  шагу  4.

Шаг  3 .  Точку  заменить  на  ,  если,  и  на  ,  если  ,  что  даёт  новое  множество  из    точек.  Перейти  к  шагу  1.

Шаг  4 .  Если 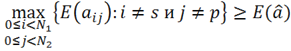 ,  то  заменить  на,  получить  новое  множество  из  точек  и  перейти  к  шагу  5.

Шаг  5 .  Взять,  для  которого  ,  и  положить  .  Если  ,  то  заменить  на    для    и  перейти  к  шагу  1.  Если  ,  то  заменить  на,  получить  новое  множество  из  точек  и  перейти  к  шагу  1.

Погрешность  метода

Пусть  эвристические  значения  по  и  определяются  по  следующими:

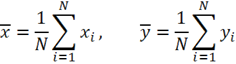
И  соответствующие  отклонения:

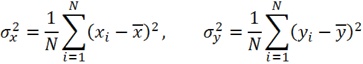
Либо

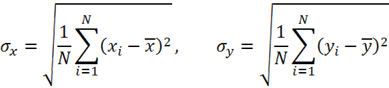
Отклонение  интерполяционной  функции:

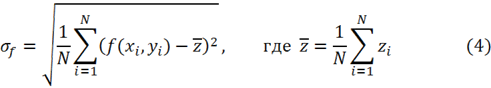
Средняя  погрешность  в  узлах  интерполяции:

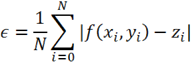
Критерий  (4)  позволяет  оценить  погрешность  метода.  Скорость  сходимости  метода  зависит  от  скорости  сходимости  метода  Ньютона  либо  метода  Нелдера-Мида.

Алгоритм  решения

Шаг  1.   Подбор  базиса  функций  и  построение  пробуемой  функции.

Шаг  2.   Построение  функционала  энергии  (2).

Шаг  3.   Нахождение  условий  для  того  чтобы  функционал  (2)  достиг  минимума.

+  Если  функционал  энергии  содержит  не  более  2-ух  параметров:  Решение  системы  уравнений  (3)  с  помощью  метода  Ньютона  для  нахождения  стационарных  точек.  Рассмотрение  знаков  частных  производных  2-ого  порядка  в  стационарных  точках  для  нахождения  значений  параметров,  с  которыми  функционал  энергии  (2)  достигает  минимума. 

+  Если  функционал  энергии  содержит  более  2-ух  параметров:  Нахождение  минимума  функционала  (2)  с  помощью  метода  Нелдера-Мида.

Пример .  Заданы  наборы  данных

Найти  поверхностную  интерполяционную  функцию  предлагаемым  методом.

Пробуемая  функция  выбирается  по  следующему  правилу:

Функционал  энергии  определяется  по  (2)  и  получается:

Для  нахождения  параметров  надо  решить  следующую  систему  уравнений:

И  получается.  Видим,  что

Следовательно,  точка  минимум.  Поверхностная  интерполяционная  функция  имеет  вид: 

Эвристические  значения  по  и: 

И  соответствующие  отклонения: 

Отклонение  поверхностной  интерполяционной  функции  и  средняя  погрешность  в  узлах  интерполяции: 

Экспериментальные  результаты 

В  нашей  программе  выбранные  наборы  данных  выполняют  правило  . 

Графики  данных  (точечный  вид)  и  интерполяционной  функции  (сеточный  вид)  при  случае  полиномиального  базиса  показаны  на  (рис.  1);  а  тригонометрического  базиса  показаны  на  (рис.  2). 

Из  полученных  результатов  видим,  что  точность  результата  аппроксимации  зависит  от  схожести  закона  распределения  данных  и  выбранного  базиса  функций.  Если  задано  достаточно  большое  количество  базисных  функций,  результат  будет  лучше.

Рисунок  1.  Полиномиальный  базис  функций  ()

Рисунок  2.  Тригонометрический  базис  функций  ()

Заключение

В  этой  работе  предлагается  метод  интерполяции  на  основе  принципа  наименьших  квадратов.  Преимущество  предлагаемого  метода  —  простое  выполнение,  высокая  точность  (зависит  от  базиса  функций),  быстрая  скорость  выполнения  зависит  от  скорости  выполнения  выбранного  итерационного  метода  (как  метод  Ньютона),  либо  метода  Нелдера-Мида.  Достоинство  нашего  метода  —  из  заданных  данных,  нам  надо  выбрать  базис  функций  и  пробуемую  функцию  такие,  что  они  имеет  одинаковый  закон  распределения  с  данными.  В  случае  неправильного  выбора  базиса  функций,  поверхностная  интерполяционная  функция  может  быть  не  найдена  (минимум  функционала  энергии  не  существует)  либо  погрешность  большая. 

Список  литературы:

1.Самарский  А.А.,  Гулин  А.Б.  Численные  методы  //  Физико  математической-литературы,  С.  190—207,  1989.

2.Gruen  A.,  D.  Akca.  Least  squares  3D  surface  matching  //  ISPRS  Journal  of  Photogrammetry  and  Remote  Sensing,  —  Vol.  59,  —  P.  151—174,  —  2005.

3.Burmen  A.,  Puhan  J.,  Tuma  T.  Grid  restrained  Nelder–Mead  algorithm  //  Computational  Optimization  and  Applications  34  (2006),  359—375.

4.Conn  A.R.,  Scheinberg  K.,  Vicente  L.N.  Introduction  to  Derivative-Free  Optimization  //  SIAM,  Philadelphia,  2009.

5.Greiner  G.,  H.P.  Seidel.  Modeling  with  triangular  B-splines  //  IEEE  Computer  Graphics  and  Applications,  14(2):56–60,  Mar.  1994. 

6.Smyth  G.K..  Nonlinear  regression  //  Encyclopedia  of  Environmetrics,  —  Vol.  3,  —  P.  1405—1411,  —  2002.

7.Prautzsch  H.,  W.  Boehm,  M.  Paluszny.  Bezier  and  BSpline  Techniques  //  Springer  Verlag,  October  2002.

8.Fuchs  H.,  Z.M.  Kedem,  S.P.  Uselton.  Optimal  surface  reconstruction  from  planar  contours  //  Magazine  Communications  of  the  ACM,  —  Vol.  20,  —  P.  693—702,  —  1977. 

9.Han  L.,  Neumann  M.  Effect  of  dimensionality  on  the  Nelder–Mead  simplex  method  //  Optimization  Methods  and  Software  21  (2006),  1—16.

10.Hensley  D.,  Smith  P.,  Woods  D.  Simplex  distortions  in  Nelder–Mead  reflections  //  IMSL  Technical  Report  Series  №  8801,  IMSL,  Inc.,  Houston,  Texas  (1988).

11.Hoppe  H.,  T.  DeRose,  T.  Duchamp,  J.  McDonald,  W.  Stuetzle.  Surface  reconstruction  from  unorganized  points  //  Proceeding  SIGGRAPH,  —  Vol.  92,  —  P.  71—78,  —  1992.

12.Kelley  C.T.  Detection  and  remediation  of  stagnation  in  the  Nelder–Mead  algorithm  using  a  sufficient  decrease  condition  //  SIAM  Journal  on  Optimization  10  (1999),  43—55.

13.Franssen  M.,  R.C.  Veltkamp,  W.  Wesselink.  Efficient  evaluation  of  triangular  B-spline  surfaces  //  Computer  Aided  Geometric  Design,  17:863—877,  2000.

14.Kazhdan  M.,  M.  Bolitho,  H.Hoppe.  Poisson  surface  reconstruction  //  Eurographics  Symposium  on  Geometry  Processing,  2006. 

15.Fong  P.,  H.P.P.  Seidel.  Control  points  for  multivariate  B-spline  surfaces  over  arbitrary  triangulations  //  Computer  Graphics  Forum,  10(4):309—317,  1991.

16.Miller  S.J..  The  method  of  least  squares  //  Web  William,  Brown  University,  Providence,  RI  02912,  2012.