ОЦЕНКА  ЭФФЕКТИВНОСТИ  ФУНКЦИОНИРОВАНИЯ  МЕЖДУНАРОДНЫХ  ЛОГИСТИЧЕСКИХ  СИСТЕМ

Халипова  Наталья  Владимировна

канд .  техн.  наук,  доцент,  доцент  кафедры  транспортних  систем  и  технологий

Академия  таможенной  службы  Украины,  Украина,  г.  Днепропетровск

E-mail:  

EVALUAT ION  OF  THE  INTERNATIONAL  LOGISTICS  SYSTEMS’  EFFECTIVENESS

Khalipova  Natalia

associate  Professor,  PhD.  tehn.  Sciences,  Associate  Professor  of  Transport  Systems  and  Technologies  Ukrainian  Academy  of  Customs,  Ukraine,  Dnepropetrovsk

АННОТАЦИЯ

Целью  статьи  является  формирование  методологического  подхода  к  определению  показателей  эффективности  логистических  систем  на  основе  теории  функций  множеств  и  множественных  объектов,  подходов  векторной  оптимизации  и  дискретного  принципа  максимума  для  многоэтапных  процессов  (в  методе  фаз). 

Модель  логистической  системы  представлена  множественным  объектом,  который  характеризуется  гибридной  суперпозицией.  Для  определения  эффективной  схемы  доставки  грузов  применен  дискретный  принцип  максимума  с  использованием  векторного  критерия  оптимизации.

ABSTRACT

The  purpose  of  this  paper  is  the  formation  of  a  methodological  approach  to  the  definition  of  logistics  systems’  performance  indicators,  based  on  the  theory  of  functions  and  sets  of  multiple  objects,  vector  optimization  approaches  and  discrete  maximum  principle  for  multistage  processes  (phase  method). 

A  logistic  system  is  shown  as  multiple  object.  which  is  characterized  by  a  hybrid  superposition.  To  determine  the  effective  delivery  of  goods  scheme  applied  discrete  maximum  principle  using  vector  optimization  criterion.

Ключевые  слова:  эффективность  логистических  систем;  множественные  объекты;  векторная  оптимизация;  дискретный  принцип  максимума.

Keywords:  efficiency  of  logistics  systems;  multiple  objects;  vector  optimization;  discrete  maximum  principle.

На  протяжении  последнего  десятилетия  к  цепи  поставок  приковано  постоянно  возрастающее  внимание  специалистов  в  связи  с  осознанием  ценности,  которая  может  быть  получена  при  интегрированном  и  стратегическом  подходе  к  ее  формированию.  Отсюда  —  стремление  к  улучшению  работы  всей  цепи  поставок,  а  не  усовершенствованию  отдельно  выполняемых  ею  логистических  функций  [3],  необходимость  формирования  интегрированной  системы  показателей  функционирования,  которая  теоретически  позволяет  направить  усилия  для  достижения  всех  целей  цепи  поставок.  В  работе  [3]  проанализированы  основные  причины  внедрения  измерителей  функционирования  в  организации,  предложены  методологические  подходы  для  выявления  подходящих  систем  измерения  и  их  реализации  для  организационных  структур. 

Работа  [4]  посвящена  проблеме  выбора  лучших  альтернатив  в  процессе  проектирования  транспортно-технологической  схемы  доставки  грузов  на  основе  формирования  множества  альтернативных  систем  их  доставки.  Для  проектирования  оптимальной  транспортно-технологической  системы  доставки  грузов  авторами  предложена  методика  формирования  альтернативных  комбинаций  разных  видов  транспорта  для  каждого  заказа.

В  работе  [6]  предложена  модель  макрологистической  системы,  представленная  на  множестве  задач  и  сформулированная  как  задача  векторной  оптимизации.  Выбор  оптимального  варианта  осуществляется  на  основе  минимизации  времени  реализации  логистического  процесса  на  всей  цепи  поставки,  минимизации  общих  затрат  и  в  максимальном  удлинении  жизненного  цикла  логистических  услуг.

Каждая  из  практически  решаемых  задач  требует  использования  различных  методов  оптимизации.  Идея  оптимизации  заключается  в  получении  наилучших  результатов  при  условии  существования  определенных  ограничений  в  системе  и  связана  со  стремлением  к  усовершенствованию  деятельности  людей  в  технической,  технологической  или  же  экономической  сферах.  Важной  и  сложной  проблемой  является  выбор  наиболее  подходящего  метода  для  решения  конкретной  задачи  среди  множества  существующих  методов  оптимизации.  Учитывая  сложность  систем,  которые  подлежат  исследованию  и  анализу,  часто  возникает  необходимость  использования  нескольких  методов  одновременно  [8]. 

Методы  оптимизации  могут  быть  применены  в  разных  областях  человеческой  деятельности,  которая  может  иметь  как  дискретную  структуру,  так  и  непрерывную.  Многоэтапный,  или  фазовый,  процесс  в  общем  случае  может  быть  описан  разностными  уравнениями.  Во  многих  случаях  непрерывный  процесс  может  рассматриваться  как  такой,  что  осуществляется  поэтапно.  И  тогда  задача  оптимизации  сводится  к  определению  значений  управляющих  переменных  на  каждом  этапе,  которые  бы  максимизировали  функцию  цели  для  многоэтапного  процесса.  В  работе  [5]  предложено  рассмотрение  детерминированных  процессов.  Многоэтапный  процесс  рассматривается  как  совокупность  определенного  количества  этапов,  тип  которых  и  способы  соединения  полностью  определяют  его  природу.  Каждый  этап  может  представлять  собой  реальный  или  же  абстрактный  объект,  в  котором  происходят  определенные  изменения.  Переменные,  которые  трансформируются  на  каждом  этапе  называют  переменными  состояния.  Желаемые  изменения  переменных  состояния  достигают  с  помощью  управляющих  переменных,  которые  принимают  постоянными  на  каждом  этапе  процесса.  Изменения  же  на  каждом  из  этапов  полностью  определяются  системой  уравнений  преобразований.

Этапы,  которые  образуют  процесс,  можно  разделить  на:  соединительные  (с  одним  входом  и  одним  выходом);  разделительные  (с  одним  входом  и  несколькими  выходами);  смесительные  (с  несколькими  входами  и  одним  выходом)  и  сложные  (с  несколькими  входами  и  выходами).  Простой  многоэтапный  процесс  состоит  только  из  соединительных  этапов.  Сложный  процесс  предусматривает  наличие  других  видов  этапов  в  процессе.  При  этом  процесс  может  содержать  более  чем  один  начальный  и  конечный  этап.

В  задачах  оптимизации  многоэтапных  управляемых  процессов  функция  цели,  которая  подлежит  максимизации  или  минимизации,  может  быть  представлена  как  функция  переменных  состояния  на  выходе  последнего  этапа.  Задача  может  быть  сформулирована  следующим  образом:  для  процесса  с  известными  уравнениями  преобразования  и  заданными  начальными  и  (или)  конечными  значениями  некоторых  переменных  состояния  найти  на  каждом  этапе  такие  значения  управляющих  переменных,  которые  удовлетворяют  заданным  ограничениям,  при  которых  функция  цели  достигает  максимума  (минимума).

Задачи  продвижения  материальных  потоков  в  логистике  можно  рассматривать  как  многоэтапный  (фазовый)  процесс.  Вместе  с  этим,  они  относятся  к  разным  функциональным  областям  и  требуют  комплексного  рассмотрения  на  основе  многих  критериев  для  рационального  и  (или)  оптимального  использования  ресурсов  во  всей  логистической  системе.  Это  обуславливает  необходимость  использования  векторного  критерия  при  оптимизации.

Целью  исследования  является  формирование  теоретических  подходов  к  определению  показателей  эффективности  логистических  систем  на  основе  теории  функций  множеств  и  множественных  объектов,  подходов  векторной  оптимизации  и  применения  дискретного  принципа  максимума  для  многоэтапных  процессов  (в  методе  фаз)  [1,  2,  7]  и  обоснования  наиболее  эффективных  схем  доставки  грузов  (товаров). 

Представим  логистическую  систему  доставки  грузов  в  виде  нескольких  последовательных  этапов  (фаз).  На  каждом  этапе  рассматривается  множество  дискретных  наборов  мероприятий,  которое  включает  возможные  технологические  циклы  операций  при  обработке  груза.  На  каждом  из  этапов  многофазного  процесса  доставки  груза  от  поставщика  к  потребителю  эти  множества  разные  и  образуют  множество  наборов  (списков)  технологических  операций  ,  доступных  к  альтернативному  или  совместному  выбору  на  каждом  из  этапов.  Каждый  из  этапов  содержит  набор  технологических  операций  ,  где  —  количество  этапов,  которые  определяются  индексом  .  Индексом    обозначены  возможные  наборы  операций  на  этапе  .  Каждая  из  операций  выбранного  технологического  цикла  обозначается  индексом  .  Технологические  операции  подлежат  выбору  на  основе  алгоритмов    на  каждом  из  этапов  .  Логистическая  система    состоит  из  множества  цепей  поставок,  которые  формируются  на  основе  списков    и  представляют  собой  возможные  варианты  доставки  грузов.  Чтобы  избрать  наиболее  эффективный  вариант  сформулируем  векторный  критерий,  где  каждой  из  цепей    из    соответствует  время  доставки  T  (),  стоимость  доставки  C  (),  которые  должными  быть  по  возможности  меньшими,  и  продолжительность  жизненного  цикла  логистической  услуги    (),  которую  нужно  максимально  продлить.  Запишем  критерий  в  виде

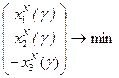,  (1)

где  . 

Особенностью  задачи  в  данной  постановке  есть  то,  что  показатели  являются  функциями  множественных  объектов,  представленных  списками,  множествами,  мультимножествами,  кортежами.  На  каждом  из  этапов  продвижения  материальных  потоков  состав  множественных  объектов  может  варьироваться  и  зависит  от  выбранного  комплекса  операций  в  процессе  складирования,  транспортировки,  таможенного  оформления  и  др.  Набор  технологических  операций  на  каждом  из  этапов  может  зависеть  от  принятого  на  предыдущем  шаге  решения  и  приводить  к  изменениям  логистической  цепи  на  дальнейших  этапах,  что  влияет  на  оценку  эффективности  доставки  в  целом. 

Для  обеспечения  требований  (1)  модель  логистической  системы  представим  как  множественный  объект  ,  который  характеризуется  гибридной  суперпозицией  (структурой),  включающей  множества,  мультимножества,  упорядоченные  множества  (списки)  и  неоднородные  множества  (последовательности,  кортежи)  [1].

Под  множеством  понимают  свободный  набор  разных  однотипных  элементов,  которые  входят  в  множество  в  произвольном  порядке.  Изменяя  свойства  набора  и  элементов  множественной  структуры,  получим  другие  объекты.  Если  в  множестве  снять  ограничения  по  разным  элементами,  то  получим  мультимножество.  Несвободный  однотипный  набор  разных  элементов  по  некоторым  отношениям  образует  упорядоченное  множество  (список),  в  случае  повторяемости  элементов  в  наборе  имеем  мультисписок.  Если  набор  разнотипный,  то,  соответственно,  он  образует  неоднородную  упорядоченную  или  неупорядоченную  последовательность,  кортеж  или  мультикортеж.  Рассмотренные  объекты  задаются  на  единой  множественной  структуре    с  помощью  отношений:  тождественности,  порядка,  неоднородности  и  др.  Формально  эта  структура  может  быть  представлена 

,  (2)

где:     —  носитель  структуры,  на  компоненте    которого  строятся  множественные  объекты  и    —  алфавит  специальных  символов; 

  —  сигнатура  отношений    и  операции  суперпозиции  ; 

  —  конструктивная  аксиоматика,  которая  задает  определение,  свойства,  правила  конструирования  объектов  и  др.  [1,  7].

Для  распознавания  объектов  и  отражения  отношений  на  них  используем  обозначение:    —  множество,    —  упорядоченное  множество,    —  неоднородное  множество,    —  мультимножество.

Подробное  описание  систем  с  помощью  конечных  множеств  и  отношений  выполнены  в  работе  [2],  а  структур  —  в  статье  [1].

В  силу  дискретности  множества  этапов    задача  векторной  оптимизации  (1)  имеет  решение.

Введем  топологическое  пространство  .  На    введем  функцию  множества.  В  случае,  когда  эти  множества  содержат  одну  точку,  они  будут  представлять  собой  функции    и  .

Математически  вариацию  технологических  операций  при  формировании  логистической  цепи  на  каждом  из  этапов  движения  выражаем  операцией  симметричной  разности  двух  множеств,  которая  включает  в  себя  «игольчастую  вариацию»  по  Макшейну  [9].  Тогда  для  определения  оптимального  значения  показателей  логистической  системы  рассматривается  задача  оптимизации  функции  множеств  [2].

Для  введенного  топологического  пространства  с  мерой  используем  производную  от  функции  множеств  по  мере

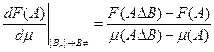
Задачу  векторной  оптимизации  можно  сформулировать  таким  образом.  Считаем,  что  цепь  «  лучше  за  »  по  показателям,  представленным  векторным  критерием  (1),  под  которым  понимаем  отношение  Парето,  если

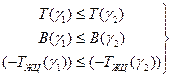  (3)

Решением  задачи  (1)  есть  некоторое  множество  несравнимых  между  собой  по  Парето  цепей  .

Два  множества    и    являются  несравнимыми,  если  среди  неравенств  (3)  имеет  место  хотя  бы  одно  строгое  противоположное  неравенство.

Согласно  (1)  определяют  привило  отбора  (критерий)  «лучших»  множеств.  Это  правило  известно  как  отношение  Парето  [2].

Для  множеств  технологических  операций    обозначим  большим  индексом  І  (римскими  цифрами)  номер  соответствующего  технологического  этапа.  Выбор  элементов  логистической  системы    при  ее  формировании  обозначаем  строчним  индексом    (арабскими  цифрами). 

При  формировании  цепи  поставок  возможны  следующие  вариации  множества:

1.  вариации  на  определенных  этапах  в  наборах  технологических  операций.  Целью  такой  модификации  в  системе  является  повышение  эффективности  или  же  оптимизация  технологического  цикла.  Такие  изменения  не  оказывают  влияния  на  эффективность  осуществления  следующих  этапов  в  выбранной  цепи  доставки  товаров  и  грузов. 

2.  вариации,  которые  происходят  при  принятии  того  или  иного  решения  на  определенном  этапе,  которые  влияют  на  все  дальнейшие  этапы  и  должны  учитываться  для  оценки  эффективности  как  каждого  из  последующих  этапов,  так  и  всей  цепи  в  целом.  Примером  такой  вариации  есть,  например,  выбор  вида  транспорта  для  доставки  или  логистического  посредника  и  др. 

Многоэтапный  процесс  может  формироваться  как  на  основе  соединительных  этапов  в  виде  простой  цепи,  так  и  с  использованием  этапов  другого  типа,  образуя  сложную  систему.  Возможно  также  рассмотрение  обратной  связи  (например,  для  учета  потоков  товаров,  которые  возвращаются  производителю). 

Формирование  цепей  поставок  показано  на  рис.  1,  где  сопоставление  каждому    множества    представляет  собой  многозначное  отображение.  Сначала  показано  формирования  всех  элементов  данной  системы  на  основе  принятия  решений  :  выбор  вида  груза  для  перевозки,  тары,  выбор  маршрута  перевозки,  потребителей,  поставщиков  и  посредников,  определение  пунктов  пропуска  пересечения  границы  между  государствами  и  пр.  Далее  изображены  этапы  (фазы)  ,  которые  проходит  груз,  перемещаясь  от  поставщика  до  потребителя,  с  отображением  циклов  технологических  операций  на  каждом  из  этапов,  избранных  на  основе  принятия  решения  .

Кругами  обведены  выбранные  в  соответствии  с  алгоритмом    элементы  многоэтапной  системы  доставки  грузов  (товаров)  без  дополнительного  выбора  технологических  операций.  Квадратами  обведены  элементы  системы,  выбор  которых  по  алгоритму    влечет  выполнение  соответствующих  технологических  операций  на  выбранных  объектах,  представленных  списками  .

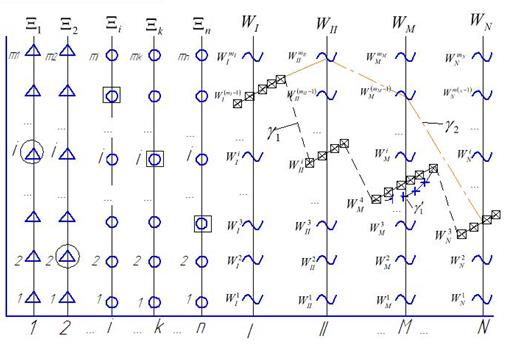
Рисунок  1.  Геометрическое  представление  многозначного  отображения 

На  рис.  1  линия  ,  которая  соединяет  объекты,  показывает  один  из  вариантов  формирования  цепи  поставок  в  логистической  системе    в  результате  принятия  решений  .  Возможная  вариация  множества  при  выполнении  определенного  технологического  цикла  обозначена  линией  .  Линия    показывает  другой  вариант  цепи  доставки,  которая  формируется  в  результате  принятия  решений  .

Уравнение  преобразования  при  перемещении  грузов  по  фазам  [5]

,  (4)

где    характеризует  состояние  на  каждом  из  этапов,  а    —  соответственно,  допустимые  управления.

Допустимые  управления

  (5) 

Начальное  состояние  .

Необходимо  найти  такие  ,  которые  удовлетворяют  (5),  чтобы 

  (6)

Введем  функцию  Гамильтона

  (7)

и  сопряженную  систему

  (8)—(9)

с  граничными  условиями

  (10)

Возможная  вариация  функции  Гамильтона

,  (11)

где    и    принадлежит  к  области  допустимых  управлений.

Теорема  1.  Оптимальное  управление    существует  для  любого  начального  состояния    и  удовлетворяет  условию

,  (12)

где    решение  (8)-(9)  с  граничными  условиями  (10).

При  этом  если    внутренняя  точка  ,  то  ,  если  граничная  точка,  то  .

Введем  множество

,

Т.  е.    —  множество  состояний,  в  которые  можно  перевести  точку    допустимыми  управлениями.

Теорема  2.  (принцип  максимума  для  дискретных  процессов).

Если  множество    выпуклое  при  любых  ,  тогда  с  необходимостью  оптимальное  управление  придает  функции  Гамильтона  максимальное  значение  по  .

Если  функция  цели  имеет  вид

,

то  выпуклость  множества

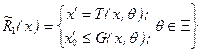
обеспечивает  справедливость  принципа  максимума  и  для  таких  задач. 

Если    ,  а  функция  цели

,

где    и    выпуклые  вверх  по  своим  переменным  и    —  выпуклое,  то  имеет  место  теорема  3.

Теорема  3.  Для  того,  чтобы  управление    было  оптимальным,  необходимо  и  достаточно,  чтобы  функция  Гамильтона  принимала  максимальное  значение  на  этом  управлении.

Пример  применения  метода  фаз.

Пусть  доставка  грузов  осуществляется  его  прохождением  через    фаз.  В  каждой  фазе  имеем  набор    мероприятий  .  Множество    дискретное  и  конечное.  Каждое  мероприятие    характеризуется  затратами  времени    и  средств  .  Положим    —  затраты  времени  на    первых  фазах,  а    —  затраты  средств,  тогда  уравнения  преобразования  будут  следующими

;

с  начальными  условиями  .

Насколько  рационально  принимаем  решение  в  каждой  фазе  будем  оценивать    и    суммарными  затратами  времени  и  средств,  соответственно.

Желательно,  чтобы    и    были  по  возможности  меньшими.

Другими  словами,  приходим  к  задаче  векторной  оптимизации

.

Введем  показатель 

Функция  Гамильтона  будет  следующей

.

Сопряженные  переменные    и    определяются  отношением

;  ,

при  этом

;  ,

тогда  .

Функция  Гамильтона  в  этом  случае  принимает  вид

.

минимальное  значение  которой  по  решениям,  которые  принимаются,  определяются  следующим  образом

.

Очевидно,  что    будет  существенно  зависеть  от  ,  а  в  силу  уравнений  преобразований  получаем  ,  при  .  Исключая  ,  получаем    и  тем  самым  получаем  решение  задачи  векторной  оптимизации. 

Рассмотрим  пример  функционирования  системы  доставки  грузов  фирмами  .

Пусть  у  фирм    есть  склады  ,  на  которых  хранятся  товары  .  Товары  доставляются  потребителю  в  контейнерах    транспортными  средствами  (автомобилями,  поездами,  воздушными  и  водными  судами).  Процесс  доставки  товаров  проходит  несколько  этапов. 

Рассмотрим  простой  процесс,  который  состоит  из  четырех  этапов: 

1) выбор  контейнеров  и  их  загрузка  товарами  на  складах, 

2) выбор  вида  транспорта  и  отгрузка  контейнеров  со  складов, 

3) второй  выбор  вида  транспорта  и  прохождение  таможенного  контроля, 

4) третий  выбор  вида  транспорта  и  перегрузка  на  выбранный  транспорт  для  доставки  товаров  на  склад  потребителя  или  прямая  доставки  товаров  на  склад  потребителя.

Каждый  из  этапов  процесса  доставки  товаров  связан  с  технологическими  операциями  обработки  грузов,  алгоритмами  выбора  и  принятия  решений.  Анализ  составных  частей  процесса  показывает,  что  в  этом  процессе  используются  множества  разных  типов:  списки  (склады  и  операции),  мультимножества  (контейнеры,  операции,  транспорт),  поэтому  логистические  модели  функционирования  системы  доставки  товаров  фирмами    целесообразно  представлять  с  помощью  специализированной  и  интерпретированной  множественной  структуры  (2).

Компонента    носителя  (логистической)  структуры  (2)  составленная  из  множеств:  складов  ,  товаров  ,  контейнеров  ,  транспортных  средств  ,  используемых  фирмами,  операций    обработки  грузов  на  определенных  этапах  технологического  процесса,  алгоритмов    (  —  входное  множество,  —  множество  решений)  выбора,  принятия  решений  и  перехода  на  следующий  технологический  этап. 

Поскольку  фирмы  могут  иметь  разные  технологические  процессы  доставки  товаров,  то  соответствующие  им  интерпретированные  множественные  объекты  будут  также  разными.  Пусть  для  фирмы    множественный  объект  —    отражает  технологию  обработки  товаров  и  грузов  при  международных  доставках,  и  его  структура  задается  формой:

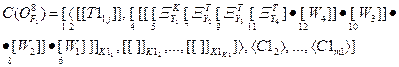,  (13)

в  которой  обозначение    определяет  список  складов,    —  мультимножество  их  содержаний:  неоднородные  множества  товаров    и  списки  контейнеров  .  При  этом  контейнер    подвергается  выбору  (вид  контейнера  или  транспортного  средства),  по  определенным  спискам  алгоритмов    и  упорядоченной  операционной  обработке  на  каждом  технологическом  этапе  .  Связь  списков  алгоритмов    и  соответствующих  операций  ,  представлена  через  операцию  последовательного  выполнения  .

Содержанием  объекта    являются  товары,  алгоритмы  выбора  и  принятие  решений,  а  также  операции  на  четырех  этапах  технологических  процессов.

Рассмотрим  численный  пример  доставки  груза  от  поставщика  А  к  потребителю  В.  Принимаем  число  фаз  N=4.  Количество  операций  в  каждой  фазе  определяется  вектором  .  Затраты  времени  (количество  суток)  для  выполнения  каждого  из  технологических  циклов  заданые  с  помощью  матрицы  .  Затраты  средств  (тыс.  у.  д.  е.)  на  выполнение  соответствующих  операций  заданы  в  матрице  :

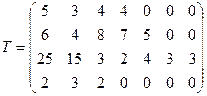
Реализация  метода  фаз  осуществлена  в  среде  Maple-7. 

Полученные  селекторы    доставки  груза  от  А  до  В,  а  также  значения  параметра  ,  затраты  средств  на  доставку    и  время  доставки  для  каждого  из  селекторов  приведены  в  табл.  1.

Таблица  1.

Варианты  доставки  груза  от  поставщика  А  к  потребителю  В

В  результате  решения  задачи  векторной  оптимизации  имеем  функционал  (рис.  2),  который  отображает  зависимость  между  временем  выполнения  операций  и  их  стоимостью  и  является  решением  задачи  векторной  оптимизации.  При  выборе  варианта  из  области  эффективных  решений  видим,  что  увеличение  времени  доставки  дает  экономию  средств,  в  то  время  как  экономия  времени  ведет  к  росту  затрат  на  доставку  груза. 

Выводы.

В  статье  логистическая  система  доставки  грузов  представлена  в  виде  многоэтапного  (фазового)  процесса.  На  каждом  этапе  рассматривается  множество  дискретных  наборов  мероприятий,  которое  включает  возможные  технологические  циклы  операций  при  обработке  груза.  На  каждом  из  этапов  многофазного  процесса  доставки  груза  от  поставщика  к  потребителю  эти  множества  разные. 

Рисунок  2.  Результат  решения  задачи  векторной  оптимизации

В  статье  предложен  теоретический  подход  на  основе  теории  функций  множеств  и  множественных  объектов,  подходов  векторной  оптимизации  и  дискретного  принципа  максимума  для  многоэтапных  процессов  (в  методе  фаз)  к  определению  показателей  эффективности  логистических  систем  и  обоснованию  наиболее  эффективных  схем  доставки  грузов  (товаров). 

Модель  логистической  системы  представлена  множественным  объектом  ,  который  характеризуется  гибридной  суперпозицией  (структурой),  составленной  из  множеств,  мультимножеств,  упорядоченных  множеств  (списков)  и  неоднородных  множеств  (последовательностей,  кортежей),  которые  представляют  на  каждом  из  этапов  наборы  технологических  операций  обработки  грузов,  алгоритмы  выбора  и  принятия  решений.

Для  определения  эффективной  схемы  доставки  грузов  с  целью  рационального  и  (или)  оптимального  использования  ресурсов  во  всей  логистической  системе  применен  дискретный  принцип  максимума  с  использованием  векторного  критерия  при  оптимизации.

Приведен  пример  применения  метода  фаз  с  использованием  дискретного  принципа  максимума  для  анализа  четырехэтапного  процесса  доставки  грузов  в  международной  логистической  системе.  Решена  задача  векторной  оптимизации  по  критерию  минимальной  стоимости  и  времени  доставки 

Список  литературы:

1.Босов  А.А.  Структурная  сложность  систем  /  А.А.  Босов,  В.М.  Ільман  //  Вестник.  ДНУЗТ.  —  2012.  —  Вип.  40.  —  С.  173—179.

2.Босов  А.А.  Функции  множеств  и  их  применение:  Монография.  Днепродзержинск:  Издательский  дом  «Андрей»,  2007.  —  182  с.

3.Линда  Натхолл  Системы  измерения  эффективности  цепи  поставок  //  Управление  цепями  поставок:  Справочник  издательства  Gover  [Под.  ред.  Дж.  Гатторны  (ред.  Г.  Огулин,  М.  Рейнольдс)]:  Пер  с  5-го  англ.  изд.  2008.  М.:  ИНФРА-М.  ХХХIV.  —  C.  316—339.

4.Наумов  В.С.  Методика  формирования  альтернативных  транспортно-технологічних  систем  доставки  грузов  /  В.С.  Наумов,  Н.С.  Ветер  //  Восточно-Европейский  журнал  передовых  технологий.  Математика  и  кибернетика  —  фундаментальные  и  прикладные  аспекты.  —  2011.  —  №  5/4  (53).  —  C.  16—19.

5.Фан  Лянь-Цэнь,  Дискретный  принцип  максимума.  Оптимизация  многоступенчатых  процессов  /  Фан  Лянь-Цэнь,  Ван  Чу-Сен.  перевод  с  англ.,  [Под  ред.  А.И.  Пропоя].  М.:  Мир,  1967.  —  181  с.

6.Халипова  Н.В.  Моделирование  логистических  систем  международных  перевозок  //  Вестник  Восточно-Украинского  Национального  университета  имени  Владимира  Даля.  —  2013.  —  №  5  (194).  —  Ч.  2.  —  C.  73—80.

7.Atkin  R.Н.  Mathematical  structure  in  human  affairs  /  London:  Heinemann.  1974.  —  212  p.

8.Lee  E.S.  Optimum  Design  and  Operation  of  Chemical  Processes  //  Ind.  Eng.  Chem.  —  1961.  —  Vol.  55,  —  №  8.  —  P.  37.

9.McShaine  E.J.  On  multipliers  for  Lagrang  problems  //  Amer.  J.  Math.  —  1939.  —  Vol.  61.  —  P.  809—819.