АЛГОРИТМ  ФИЛЬТРАЦИИ  ДЛЯ  ОБНАРУЖЕНИЯ  ОБЪЕКТОВ  ПО  ИЗОБРАЖЕНИЯМ,  ЗАРЕГИСТРИРОВАННЫМ  МАТРИЧНЫМ  ФОТОПРИЕМНИКОМ  В  РЕЖИМЕ  МИКРОСКАНИРОВАНИЯ

Шакенов  Адильбек  Кобланович

канд.  техн.  наук,  младший  научный  сотрудник  Института  автоматики  и  электрометрии  Сибирского  отделения  Российской  академии  наук,  РФ,  г.  Новосибирск

E -mail:  adil.shakenov@ngs . ru

Будеев  Денис  Евгеньевич

инженер-программист  Института  автоматики  и  электрометрии  Сибирского  отделения  Российской  академии  наук,  РФ,  г.  Новосибирск

E-mail: 

ALGORITHM  OF  FILTERING  FOR  DETECTION  OF  OBJECTS  IN  THE  IMAGES  REGISTERED  BY  MATRIX  PHOTODETECTOR  IN  THE  MICROSCANNING  MODE

Shakenov  Adilbek

candidate  of  Science ,  junior  researcher  of  Institute  of  Automation  and  Electrometry  SB  RAS,  Russia,  Novosibirsk

Budeev  Denis

engineer  of  Institute  of  Automation  and  Electrometry  SB  RAS,  Russia,  Novosibirsk

АННОТАЦИЯ

Предложен  алгоритм  обнаружения  объектов  на  изображениях,  полученных  в  режиме  микросканирования.  Приведено  описание  алгоритма  в  предположении  о  постоянности  формы  объекта.  Так  же  проведено  исследование  влияния  на  результат  фильтрации  изменения  формы  объекта,  вызванного  субпиксельным  смещением  объекта  относительно  центра  фоточувствительного  элемента.  Опробован  подход  к  выбору  формы  фильтра  с  учетом  изменения  формы  объекта.  Приведены  результаты  численного  моделирования.

ABSTRACT

The  algorithm  for  detecting  objects  in  images  taken  in  mode  microscanning  is  proposed.  The  description  of  the  filtering  algorithm  for  constant  object's  shape  is  presented.  Influence  of  changes  in  the  shape  of  the  object  caused  by  sub-pixel  displacement  of  the  object  relative  to  the  center  of  the  photosensitive  element  on  the  filtering  quality  is  studied.  The  approach  to  the  choice  of  the  form  of  the  filter  taking  into  account  the  changes  in  the  shape  of  the  object  is  probed.  The  results  of  numerical  modeling  are  presented.

Ключевые   слова:  малоразмерный  объект;  алгоритм  обнаружения;  микросканирование;  алгоритм  фильтрации  изображений.

Keywords:  small  objects;  detection  algorithm;  microscanning;  image  filtering.

Введение

Для  решения  задачи  детектирования  малоразмерных  объектов  используются  камеры,  регистрация  данных  в  которых  происходит  при  помощи  матричного  фотоприемника.  Фотоприемная  матрица  состоит  из  периодически  расположенных  фоточувствительных  элементов,  между  которыми  есть  межэлементные  промежутки  размером  10—50  %  от  линейного  размера  элемента.

При  попадании  проекции  малоразмерного  объекта  в  межэлементный  промежуток  матрицы  фотоприемника  происходит  уменьшение  регистрируемой  интенсивности  объекта.  Один  из  подходов  к  решению  этой  проблемы  заключается  в  использовании  систем  наблюдения,  которые  регистрируют  данные  при  помощи  микросканирования  [6,  10].  При  микросканировании  происходит  поочередное  смещение  матрицы  фотоприемника  относительно  исходного  положения,  и  регистрация  изображений  проводится  в  нескольких  позициях.  Затем  полученные  кадры  объединяются  в  одно  изображение  более  высокого  разрешения.  Существуют  различные  алгоритмы  получения  изображения  высокого  разрешения  по  последовательности  кадров,  полученных  при  микросканировании.  В  работах  [13,  14]  развит  подход  к  решению  этой  задачи  на  основе  Винеровской  фильтрации.  В  работах  [3,  4]  рассмотрены  алгоритмы  на  основе  оптимального  линейного  прогноза.  Ряд  быстрых  итеративных  и  рекуррентных  алгоритмов  изложен  в  статьях  [2,  12]. 

Малоразмерные  объекты,  представлявшие  на  исходных  кадрах  несколько  пикселов,  на  изображении  высокого  разрешения  имеют  выраженную  форму,  которая  зависит  от  параметров  системы  наблюдения  —  функции  рассеяния  точки,  размера  фоточувствительного  элемента,  а  так  же  от  траектории  смещения  матрицы  в  процессе  микросканирования.  На  рисунке  1  приведены  изображения  объектов  до  микросканирования  в  зависимости  от  их  начального  положения  относительно  элементов  матрицы.

Рисунок  1.  Объекты  до  микросканирования:  a )  Объект  №  1  попал  в  промежуток;  b)  Объект  №  2  попал  на  элемент  ФПУ

На  рисунке  2  изображены  объекты  после  объединения  кадров,  полученных  в  режиме  кругового  микросканирования.

Рисунок  2.  Объекты  после  микросканирования:  a )  Объект  №  1;  b)  Объект  №  2

Как  правило,  исходное  изображение,  на  котором  необходимо  обнаружить  объект,  состоит  из  коррелированной  фоновой  текстуры  с  дисперсией,  сопоставимой  с  амплитудой  объекта  и  случайного  некоррелированного  шума.  На  рисунке  3  приведен  пример  входного  изображения  содержащего  9  объектов.  Изображение  получено  путем  численного  моделирования.

Рисунок  3.  Фрагмент  исходного  изображения  с  объектами

Форму  объекта  можно  считать  известной,  поскольку  известны  параметры  регистрирующей  системы  и  траектория  сканирования  матрицы.  Возникает  задача  обнаружения  объекта  известной  формы  на  фоне  коррелированного  шума.  Известен  метод  линейной  фильтрации  [5],  позволяющий  получить  оптимальное  на  множестве  линейных  фильтров  решение  данной  задачи.  Однако  практическое  применение  этого  алгоритма  затруднено  из-за  высокой  вычислительной  сложности,  возникающей  при  оценке  ковариационной  матрицы  фона.  По  этой  причине  активно  исследуются  более  быстрые  алгоритмы  оценки  и  подавления  фоновой  составляющей.  В  работе  [1]  представлен  линейный  фильтр,  построенный  в  предположении  о  локальной  линейности  фона.  В  работах  [7,  8]  представлены  различные  подходы  к  задаче  подавления  фона  на  основе  билатеральной  фильтрации.  Подавление  фона  на  основе  медианной  фильтрации  предложено  в  работе  [9].  В  работе  [11]  содержится  ряд  модификаций  этого  подхода.  При  выборе  подхода  к  разработке  алгоритма  подавления  фона  нужно  учитывать  характеристики  текстуры  и  объекта.

Постановка  задачи

Необходимо  увеличить  отношение  полезного  сигнала  к  величине  среднеквадратичного  отклонения  шумов  после  обработки  за  счет  построения  фильтра,  учитывающего  форму  объекта  при  наличии  коррелированной  фоновой  текстуры  и  некоррелированного  шума.  При  этом  в  силу  вычислительных  ограничений,  сложность  алгоритма  не  должна  превышать  нескольких  операций  на  пиксел  изображения.

Алгоритм  фильтрации

В  предположении,  что  форма  объекта  постоянна  и  не  зависит  от  расположения  относительно  элементов  матрицы,  был  предложен  алгоритм  обработки,  представленный  на  рисунке  4.

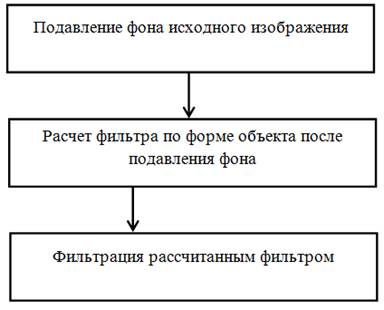
Рисунок  4.  Схема  алгоритма  обработки  для  постоянной  формы  объекта

1.  Подавление  фона  исходного  изображения

В  данной  работе  был  использован  описанный  в  [1]  алгоритм  подавления  фоновой  текстуры,  основанный  на  предположении,  что  фон  в  пределах  апертуры  фильтра  можно  считать  плоским.

Процесс  фильтрации  представляет  собой  свертку  исходного  изображения  с  импульсной  характеристикой  фильтра:

где:    —  входное  изображение, 

  —  выходное  изображение, 

—  весовые  коэффициенты.  Коэффициенты  импульсной  характеристики  фильтра  задаются  следующим  образом:

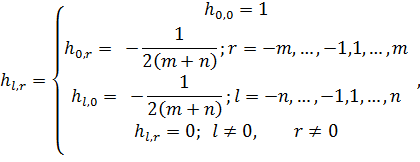
где    —  размер  окна  фильтрации.

В  работе  был  использован  фильтр  с  окном  размера  5х5,  поскольку  в  результате  численных  экспериментов  было  установлено,  что  дальнейшее  увеличение  размера,  практически  не  улучшает  качество  фильтрации.

2.  Расчет  фильтра  с  учетом  подавления  фона

Если  с  достаточной  точностью  выполняется  предположение  о  линейности  фона  в  границах  апертуры  фильтра,  то  после  этапа  подавления  фоновой  составляющей  шум  на  выходе  фильтра  в  значительной  степени  близок  к  белому,  поэтому  для  задачи  выделения  полезного  сигнала  на  фоне  шумов  используется  фильтр,  имеющий  форму  объекта.  При  этом  объект  предварительно  проходит  обработку  фильтром,  который  подавляет  фоновую  текстуру.  На  рисунке  5  показан  объект  до  и  после  обработки  фильтром,  подавляющим  текстуру  фона.

Рисунок  5.  Объект:  a )  до  обработки,  b)  после  обработки

Обработанный  объект  выступает  в  роли  фильтра  для  третьего  заключительного  шага  предлагаемого  алгоритма.

3.  Фильтрация  синтезированным  фильтром

Заключительным  этапом  фильтрации  является  обработка  синтезированным  фильтром,  полученным  на  предыдущем  этапе.  Процесс  обработки  представляет  собой  свертку  исходного  изображения,  профильтрованного  подавляющим  фильтром,  с  фильтром,  полученным  на  втором  этапе.  В  качестве  нормировочного  множителя  был  использован  квадратный  корень  из  суммы  квадратов  элементов  импульсной  характеристики  фильтра.  На  рисунке  6  представлено  исходное  изображение  с  подавленным  фоном  и  изображение  после  фильтрации  синтезированным  фильтром.

Рисунок  6.  Фрагмент  исходного  изображения:  a )  до  фильтрации,  b)  после  фильтрации

Алгоритм  выбора  фильтра  с  учетом  изменения  формы  объекта

Форма  изображения  объекта  зарегистрированного  камерой,  а  также  его  зарегистрированная  амплитуда  зависит  от  положения  проекции  центра  объекта  в  плоскости  фотоприемной  матрицы  относительно  ячеек  фотоприемника.  Поэтому  нужно  найти  фильтр,  который  в  среднем  дает  лучшие  результаты  для  всех  форм  объекта.  Для  решения  этой  задачи  был  опробован  следующий  подход.  На  изображение  были  нанесены  100  объектов,  таким  образом,  чтобы  покрыть  все  возможные  (с  точностью  до  0,1  пиксела)  положения  объекта,  относительно  центра  фотоприемного  элемента.  Объекты  были  разнесены  по  полю  кадра  с  шагом,  значительно  превышающим  размер  изображения  объекта.  Затем  это  изображение  описанным  выше  способом  было  профильтровано  каждым  фильтром  из  набора  возможных  форм  объекта.  Величина  отклика    при  фильтрации  объекта  с  номером  j  фильтром  с  номером  i  записывалась  в  массив.  Затем  рассчитывалось  среднее  значение  отклика  для  фильтра  под  номером  i:

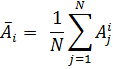
где:    —  среднее  значение  при  фильтрации  фильтром  под  номером  i;

  —  отклик  j  -го  объекта  на  i  -ый  фильтр,  (  i  =  1,  2,  ...,  N  );

N   —  число  фильтров.

В  данной  работе  N  =  100.  Затем  по  полученному  массиву  определяется  номер  фильтра,  который  дал  максимальный  отклик:

где:  k  —  номер  фильтра;

  —  среднее  значение  при  фильтрации  фильтром  под  номером  i.

Экспериментальные  результаты

Исходные  изображения,  использованные  в  экспериментах,  были  получены  при  помощи  численного  моделирования.  Они  содержали  объекты,  коррелированную  фоновую  составляющую,  имитирующую  облачный  покров,  а  также  случайное  шумовое  поле.

Для  исследования  эффективности  предложенного  алгоритма  был  проведен  следующий  эксперимент.  На  исходное  изображение,  содержащее  объекты  и  фоновую  текстуру,  аддитивно  добавлялся  случайный  шум  со  среднеквадратичным  отклонением  в  диапазоне  от  0,5  до  2,0.  Затем  проводилась  обработка  предложенным  алгоритмом.  Результаты  приведены  в  таблице  1.  В  таблице  использованы  следующие  обозначения:  —  исходная  амплитуда  объектов;  —  оцененное  среднеквадратичное  отклонение  шумов  до  обработки  (оценка  получена  по  фрагменту  изображения  не  содержащему  объектов);  —  среднее  значение  амплитуды  объектов  после  обработки;  —  оцененное  среднеквадратичное  отклонение  шумов  после  обработки  (оценка  получена  по  фрагменту  изображения  не  содержащему  объектов). 

Таблица  1.

Результаты  фильтрации  (СКО  фона  =  24,1)

Как  видно  из  таблицы,  фильтрация  с  подавлением  фона  дает  выигрыш  относительно  исходного  отношения  сигнал  /  шум  до  7  раз.

Для  иллюстрации  выбора  формы  фильтра  на  рисунке  7  приведен  график  зависимости  среднего  значения  отклика  на  объекты  при  фильтрации  различными  фильтрами.  Обработка  проводилась  в  отсутствии  фона  и  случайного  шума.

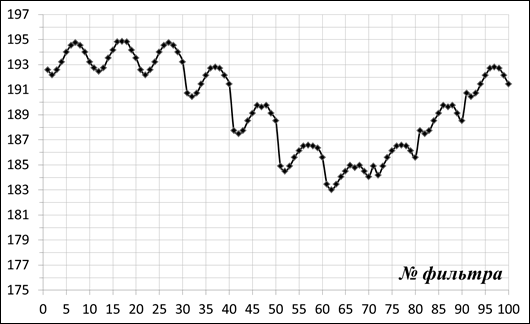
Рисунок  7.  Средний  отклик  для  различных  фильтров

Из  графика  видно,  что  в  зависимости  от  формы  фильтра  средняя  величина  отклика  значительно  меняется.  Для  получения  наилучшего  результата  фильтрации  целесообразно  использовать  фильтр,  который  дал  в  среднем  максимальный  отклик.  В  приведенном  эксперименте  это  фильтр  под  номером  17.

В  таблице  2  представлено  отношение  сигнал  /  шум  для  фильтрации  с  подавлением  фона  с  учетом  изменения  формы  объекта.  Выбор  наилучшего  и  наихудшего  фильтра  был  осуществлен  с  помощью  описанной  выше  процедуры  по  изображениям,  содержщим  объекты  без  фоновой  составляющей  и  случайного  шума.  Затем  проводилась  фильтрация  выбранными  фильтрами  изображений,  содержищих  объекты,  фоновую  составляющую  и  шум.  В  таблице  использованы  следующие  обозначения:  —  среднее  значение  амплитуды  объектов  после  фильтрации  наилучшим  фильтром;  —  оцененное  среднеквадратичное  отклонение  шумов  после  фильтрации  наилучшим  фильтром;  —  среднее  значение  амплитуды  объектов  после  фильтрации  наихудшим  фильтром;  —  оцененное  среднеквадратичное  отклонение  шумов  после  фильтрации  наихудшим  фильтром.  Оценка  среднеквадратичного  отклонения  шумов  проводилась  по  фрагменту  изображения  не  содержащему  объектов. 

Таблица  2.

Результаты  фильтрации  с  учетом  формы  фильтра  (СКО  фона  =  24,1)

По  результатам  видно,  что  выигрыш  при  выборе  формы  фильтра  составляет  до  10  %.

Заключение

Полученные  результаты  показывают,  что  предложенный  алгоритм,  основанный  на  последовательном  применении  подавления  локально  плоского  фона  и  фильтрации  согласованной  с  формой  объекта,  позволяет  значительно  увеличить  отношение  полезного  сигнала  к  уровню  шума.  В  проведенных  численных  экспериментах  было  достигнуто  увеличение  этой  величины  до  7  раз.  Известная  топология  сканирующего  устройства,  позволяет  провести  предварительный  расчет  различных  форм  объекта  с  учетом  его  субпиксельного  положения  относительно  элементов  фотоприемной  матрицы.  Результаты  моделирования  показали  необходимость  учитывать  субпиксельные  изменения  формы  объекта.  Для  рассмотренных  модельных  данных  улучшение  за  счет  выбора  наилучшей  формы  фильтра  составило  10  процентов.  Развитие  работы  может  быть  направленно  на  исследование  применения  методов  нелинейной  фильтрации  к  данной  задаче,  а  так  же  синтезу  оптимального  фильтра  по  набору  его  возможных  форм.

Список  литературы:

1.Артемьев  В.М.,  Наумов  А.О.,  Кохан  Л.Л.  Обнаружение  точечных  объектов  на  изображениях  в  условиях  неопределенности  //  Информатика  апрель-июль  2010  №  2.

2.Иванов  В.А.,  Киричук  В.С.,  Косых  В.П.,  Куликов  В.А.,  Черенкова  К.Ю.  Быстродействующие  алгоритмы  построения  изображений  с  повышенной  частотой  дискретизации  //  Автометрия  —  2009,  —  Т.  45,  —  №  5  —  с.  9—13.

3.Иванов  В.А.,  Киричук  В.С.,  Косых  В.П.  Формирование  изображения  повышенного  разрешения  по  серии  взаимно  смещенных  изображений  посредством  оптимального  линейного  прогноза  //  Автометрия  —  2009,  —  Т.  45,  —  №  2  —  с.  3—13.

4.Косых  В.П.  Коррекция  импульсного  отклика  системы  видеорегистрации  при  накоплении  серии  взаимно  смещенных  изображений  //  Автометрия  —  2009,  —  Т.  45,  —  №  5  —  с.  3—8.

5.Прэтт  У.  Цифровая  обработка  изображения  //  М.:  Мир,  1982  Кн.  2  —  480  с.,  с.  582—584.

6.Тарасов  В.В.,  Якушенков  Ю.Г.  Некоторые  пути  совершенствования  тепловизионных  систем  //  Специальная  техника  —  2004  —  №  2  —  с.  11—19.

7.Bae  T.-W.,  Lee  S.-H.,  Sohng  K.-I.  “Small  target  detection  using  the  Bilateral  Filter  based  on  Target  Similarity  Index”  //  IEICE  Electronics  Express  2010,  —  Vol.  7,  —  №  9,  —  p.  589—595.

8.Bae  T.-W.,  Sohng  K.-I.  “Small  Target  Detection  Using  Bilateral  Filter  Based  on  Edge  Component”  //  Infrared  Milli  Terahz  Waves  —  2010,  —  Vol.  31  —  p.  735—743.

9.Barnett  J.  “Statistical  Analysis  of  Median  Subtraction  Filtering  with  Application  to  Point  Target  Detection  in  Infrared  Backgrounds”  //  Proc.  SPIE,  1989,  Vol.  1050  Infrared  Systems  and  Components  III  —  p.  10—18.

10.Cabanski  W.,  Breiter  R.,  Mauk  K-H.  Miniaturized  high  performance  starring  thermal  imaging  system  //  SPIE  Proc.  —  2000,  —  Vol.  4028  —  p.  208—219.

11.Deshpande  S.D.,  Er  M.H.,  Ronda  V.,  Chan  P.  “Max-Mean  and  Max-Median  filters  for  detection  of  small-targets”  //  Proc.  SPIE,  —  1999,  —  Vol.  3809,  —  p.  74—83.

12.Lopez-Martineza  J.L.,  Kober  V.  “Fast  image  restoration  algorithm  based  on  camera  microscanning”  //  Proc.  of  SPIE,  2009,  Vol.  7443.

13.Yousef  A.,  Li  J.,  Karim  M.A.  “Mathematical  model  development  of  super-resolution  image  Wiener  restoration”  //  SPIE  Optical  Engineering,  2012,  Vol.  51(3).

14.Yousef  A.M.,  Rahman  Z.,  Karim  M.  “On  the  restoration  of  the  microscanned  images  captured  from  unmanned  airborne  vehicles”  //  Proc.  of  SPIE,  2011,  Vol.  8056.