ПЛАНИРОВАНИЯ  МАРШРУТА  КУРЬЕРСКОЙ  СЛУЖБЫ  НА  ОСНОВЕ  АЛГОРИТМА  МУРАВЕЙНИКА

Берилло  Андрей  Викторович

студент  5  курса  специальности  «Информационные  системы  и  технологии  (в  экономике)»  факультета  экономики  и  управления  Гродненского  государственного  университета  имени  Янки  Купалы,  Республика  Беларусь,  г.  Гродно

E -mail:  andrey.berillo@gmail.com

Степин  Юрий  Генрихович

старший  преподаватель  кафедры  математического  и  информационного  обеспечения  экономических  систем  факультета  экономики  и  управления  Гродненского  государственного  университета  имени  Янки  Купалы,  Беларусь,  г.  Гродно

E-mail:  stepin@ grsu.by.

ROUTE  PLANNING  OF  COURIER  SERVICE  BASESD  ON  ANT  ALGORITHM

Andrew  Berillo

student  of  5th  course  “Information  Systems  and  Technologies  (in  the  economy) ”   Economics  and  Management  Faculty  of  Grodno  State  University  named  Yanka  Kupala,  Republic  of  Belarus,  Grodno

Yuri  Stepin

senior  Lecturer  of  mathematical  and  information  systems  and  economic  systems  department  of  the  Faculty  of  Economics  and  Management  Grodno  State  University  named  Yanka  Kupala,  Republic  of  Belarus,  Grodno

АННОТАЦИЯ

В  статье  проанализированы  методы  решения  задачи  планирования  маршрута  курьерской  службы  на  основе  алгоритма  муравейника.  Выделены  основные  коэффициенты  используемые  в  муравьином  алгоритме,  сделана  оценка  влияния  данных  коэффициентов  на  эффективность  алгоритма  и  его  сходимость.

ABSTRACT

The  article  analyzes  the  metaheuristic  methods  for  solving  the  route  planning  of  courier  service.  Identified  the  main  factors  used  in  ant  colony  algorithms.  The  estimation  of  the  influence  of  these  coefficients  on  the  performance  of  the  algorithm  and  its  convergence.

Ключевые  слова:  муравьиный  алгоритм;  планирование;  маршрут.

Keywords:  ant  algorithm;  planning;  route.

Введение.  Динамика  расширения  рынка  транспортно-логистических  услуг,  наблюдаемая  в  последнее  время,  открытие  новых  логистических  терминалов,  усиление  соперничества  между  операторами  способствуют  росту  потребности  в  комплексном  решении  транспортно-логистических  задач  в  целях  более  эффективного  обслуживания  клиентов.

Часто  диспетчер  тратит  много  часов  и  даже  дней  на  решение  задачи  оптимизации  перевозок,  используя  для  этого  различные  неспециализированные  компьютерные  программы.  Как  известно,  эти  программы  не  могут  учесть  всех  реально  существующих  параметров  и  требований,  которые  налагают  на  них  грузоотправители,  транспортные  средства,  грузополучатели,  реальная  средняя  скорость  передвижения  по  автодорогам  и  иные  факторы.  При  этом  сложность  транспортной  сети  возрастает  по  мере  увеличения  числа  ее  объектов  (склад,  грузоперевозчик,  грузоотправитель,  продукты)  и  числа  бизнес-ограничений  (график  работы  объектов,  характеристики  транспортных  средств,  маршрутов,  скорость  на  автотрассах  и  т.  д.).  Уменьшается  наглядность  схемы  взаимодействия,  и  выбор  оптимального  решения  становится  сложной  задачей,  решить  которую  без  специализированных  компьютерных  программ  практически  невозможно.  В  результате  диспетчер  упускает  принципиальные  моменты,  которые  существенно  влияют  на  реальную  стоимость  транспортировки  [1,  с.  91].

Для  таких  задач  разумно  использовать  эвристические  алгоритмы,  которые  быстро  находят  хорошие,  хотя  и  не  обязательно  оптимальные,  решения.  Эти  алгоритмы  часто  используют  некоторые  знания  специфически  задач  либо  для  построения,  либо  для  улучшения  решений.  В  последнее  время  многие  исследователи  сосредоточили  свое  внимание  на  новом  классе  метаэвристических  алгоритмов  [2].

Алгоритм  муравейника.  Муравьиные  колонии  существуют  без  централизованного  управления,  где  каждый  отдельный  муравей  сам  принимает  решения  насчет  своих  дальнейших  действий.  Принятию  разумных  решений  муравья  способствует  феромон  откладываемый  другими  особями  колонии.  Основная  идея  алгоритма  заключается  в  том,  что  по  более  коротким  путям  муравьи  будут  передвигаться  чаще,  чем  по  более  длинным,  а  значит  откладывать  феромон  будут  чаще  на  более  коротких  путях.  Например:  если  два  муравья  в  одно  и  то  же  время  выйдут  из  начального  пункта  в  конечный,  причем  первый  выберет  путь  в  два  раза  короче  чем  второй,  то  за  тот  период  времени,  что  понадобится  второму  чтобы  вернуться  в  начальную  позицию,  первый  муравей  сумеет  дважды  пройти  путь  туда  и  обратно,  отложив  на  короткий  путь  феромон  4  раза,  против  2-ух  раз  второго  муравья.

Эта  идея  может  эффективно  масштабироваться  для  решения  разнообразных  транспортных  задач  с  таким  же  успехом,  а  может  даже  и  лучше  чем  существующие  эвристические  алгоритмы  [3,  4].

Содержательная  постановка.  Для  планирования  маршрута  курьерской  службы  нужно  решить  задачу  последовательного  упорядочения  пунктов  следования.

Есть  множество  контрольных  точек  на  карте,  а  также  множество  заявок  для  перевозок,  в  которых  указывается  с  какой  точки  в  какую  и  сколько  груза  нужно  перевести.  Известны  расстояния  между  точками.  В  одну  и  ту  же  точку  можно  возвращаться  неограниченное  число  раз.  Емкость  транспортного  средства  ограничена.  Если  в  вершине,  где  он  сейчас  находится,  есть  груз,  который  нужно  переместить  по  заявке,  он  может  взять  этот  груз,  причем  взять  может  как  полностью  весь,  так  и  часть  от  него.

Главная  цель  —  минимизировать  расходы  на  перевозки  груза  по  всем  заявкам,  где  расходы  напрямую  зависят  от  пройденного  пути  и  массы  перевозимого  на  этом  пути  груза.

Формальная  постановка.  Есть  транспортное  средство  грузоподъемностью  —  QN.  Множество  точек  ,  i[0,  N].  Дан  взвешенный  граф  с  количеством  вершин  N,  где  каждая  вершина  соответствует  контрольной  точке,  а  вес  ребра  —  длине  пути  из  одной  точки  в  другую.  Кроме  того  существуют  заявки    (,  ,  v),  где  k[0,  M],  —  вершина  где  находится  груз,  —  вершина  куда  необходимо  доставить  груз,  v  —  масса  груза  в  заявке.

Задачу  оптимизации  перевозок  груза  можно  сформулировать  как  минимизацию  стоимости  маршрута  перевозки  грузов  при  выполнении  всех  заявок,  где  под  маршрутом  понимается  последовательность  ребер  инцидентных  им  вершин  следования  перевозчика:

S  =    (1)

где:  Cij  —  длина  ребра  между  i-ой  и  j-ой  вершинами;

Qij  —  масса  транспорта  и  груза  перевозимого  по  ребру  из  i-ой  в  j-ую  вершину;

Особенности  программной  реализации.  В  первую  очередь  на  основе  исходного  графа  при  помощи  алгоритма  Флойда-Уоршелла  строится  вспомогательный  полный  граф,  где  остаются  только  те  вершины  в  которых  находятся  заявки  и  вершины  являющиеся  целью  заявок.  Ребро  полного  графа  между  двумя  вершинами  имеет  вес  равный  минимальному  пути  между  этими  вершинами  в  исходном  графе.  При  помощи  вспомогательного  графа  кратчайших  путей  можно  узнать  ценность  перехода  по  ребру.

Муравей  помещается  в  стартовую  вершину  полученного  графа,  которая  задается  вместе  с  графом.  Вначале  все  ребра  имеют  одинаковый  уровень  феромона.

Когда  муравей  решает,  в  какую  вершину  ему  перейти,  он  использует  следующую  формулу:

  (2)

где:    —  уровень  феромона  на  ребре  из  вершины  i  в  j; 

  —  длина  минимального  пути  из  j  в  k;

α,  β  —  константные  параметры.

Вероятность  перехода  в  уже  посещенную  вершину  высчитывается  по  формуле:

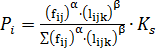  (3)

где:    —  Коэффициент  вероятности  повторного  посещения  вершин.

Формула  для  расчета  вероятности  перехода  по  последнему  пройденному  ребру  в  обратном  порядке:

  (4)

где    —  коэффициент  вероятности  обратного  хода  по  последнему  ребру.

В  случаи,  когда  муравей  заполнен  полностью  и  больше  не  в  состоянии  принять  дополнительный  груз,  он  рассматривает  только  те  варианты  переходов,  которые  позволят  ему  разгрузиться.

При  попадании  муравья  в  вершину  с  заявкой,  возможны  две  ситуации.  Первая,  когда  он  может  забрать  весь  груз  заявки.  Вторая,  когда  забрать  весь  груз  не  позволяет  текущая  емкость  муравья,  в  таком  случаи  набирается  максимально  возможный  объем  груза  по  заявке  только  если  объем  груза  по  заявке  превышает  номинальный  объем  муравья,  иначе  груз  не  забирается.  В  случаи,  если  в  вершине  находится  сразу  несколько  заявок  —  он  выбирает  их  в  любом  порядке  и  пытается  загрузиться  до  тех  пор  пока  позволяет  емкость.

После  того,  как  аналогичным  образом  все  муравьи  колонии  выполнят  все  свои  заявки  —  происходит  распределение  феромона.  Феромон  распределяется  исходя  из  отношения  лучшего  пути  показанного  в  колонии  к  некоторой  статичной  величине  пути  задаваемой  индивидуально  для  каждой  задачи  и  примерно  равной  150%  оптимального  пути. 

Формула  расчета  феромона  по  пройденному  пути  обычным  муравьем:

  (5)

где:    —  феромон  откладываемый  k-ым  муравьем  на  ребро  из  вершины  i  в  j;

Q  —  константа,  величина  для  относительной  оценки  пути  различных  муравьев;

—  длина  пути  пройденного  k-ым  муравьем;

r  —  коэффициент  отложения  феромона  обычным  муравьем.

Формула  расчета  феромона  по  пройденному  пути  элитным  муравьем:

  (6)

где  e  —  Коэффициент  отложения  феромона  элитным  муравьем.

Операции  повторяются  с  множеством  колоний,  различие  заключается  лишь  в  том,  что  муравьи  последующих  колоний  учитывают  опыт  предыдущих  колоний.

Дополнительные  коэффициенты.  После  проведения  множества  опытов  на  различных  исходных  данных,  были  сделаны  выводы,  что  классический  муравьиный  алгоритм  можно  значительно  улучшить  при  помощи  его  модификации.  Использование  дополнительных  параметров  позволяет  контролировать  скорость  сходимости  и  точность  нахождения  оптимального  маршрута.  В  зависимости  от  конкретной  поставленной  задачи  количество  используемых  параметров  может  заметно  изменяться.  Далее  приведены  коэффициенты,  используемые  для  решения  задачи  планирования  маршрута  курьерской  службы.

Альфа  (α)  —  степень  значимости  динамических  параметров  (феромон  и  т.  д.)  [0,  1].  При  увеличении  значения  —  замедляется  сходимость,  но  увеличивается  точность.  При  уменьшении  все  происходит  с  точностью  наоборот.

Бета  (β)  —  степень  значимости  статических  параметров  (расстояние)  [0,  1].  При  увеличении  значения  —  ускоряется  сходимость,  но  уменьшается  точность.  При  уменьшении  все  происходит  с  точностью  наоборот.

Коэффициент  вероятности  обратного  хода  по  последнему  ребру  ()  [0,  1].  При  уменьшении  значения  —  ускоряется  сходимость,  но  уменьшается  точность.  При  увеличении  все  происходит  с  точностью  наоборот.

Коэффициент  вероятности  повторного  посещения  вершин  ()[0,  1].  При  уменьшении  значения  —  ускоряется  сходимость,  но  уменьшается  точность.  При  увеличении  все  происходит  с  точностью  наоборот. 

Коэффициент  (Степень)  отложения  феромона  элитным  муравьем  (e)  [0,  N].  При  увеличении  значения  —  ускоряется  сходимость,  но  уменьшается  точность.  При  уменьшении  все  происходит  с  точностью  наоборот.

Коэффициент  (Степень)  отложения  феромона  обычным  муравьем  (r)  [0,  N].  При  увеличении  значения  —  ускоряется  сходимость,  но  уменьшается  точность.  При  уменьшении  все  происходит  с  точностью  наоборот.

Интервал  предельных  значений  феромона  —  необходим  для  того,  чтобы  у  ребер  не  было  нулевой  вероятности  посещения.  При  расширении  интервала  —  ускоряется  сходимость,  но  уменьшается  точность.  При  сужении  интервала  все  происходит  с  точностью  наоборот.  Уровень  феромона  не  может  превосходить  или  быть  ниже,  чем  предельные  значения  феромона,  в  случаи  выхода  за  пределы  принимает  значение  ближайшего  предельного.

Выводы.  В  связи  с  тем,  что  для  задачи  планирования  маршрута  курьерской  службы  использовать  алгоритмы  с  точным  решением  невозможно  на  больших  графах  —  был  использован  муравьиный  алгоритм.  Он  позволяет  находить  оптимальные  решения  на  графах  различной  величины.  Классический  алгоритм  не  позволяет  достаточно  успешно  находить  оптимальный  маршрут,  так  как  в  нем  не  учтено  множество  условий  и  особенностей  конкретной  задачи.  Однако  на  его  основе  удобно  строиться  модифицированный  алгоритм,  который  учитывает  особенности  задачи,  а  также  цели,  преследуемые  при  поиске  пути.  Множество  параметров  модифицированного  алгоритма  позволяет  варьировать  скорость  сходимости  и  точность.  Таким  образом,  одним  из  важнейших  факторов,  влияющих  на  успех  использования  муравьиного  алгоритма  является  грамотный  подбор  вспомогательных  параметров.

Список  литературы :

1.МакКоннелл  Дж.  Основы  современных  алгоритмов./  Дж.  МакКоннелл  //  М.:  Техносфера,  2004  —  127  c.

2.Штовба  С.Д.  Муравьиные  алгоритмы./С.Д.  Штовба//  ExponentaPro.  Математика  в  приложениях.  2004.

3.Eric  Bonabeau,  Marco  Dorigo,  and  Guy  Theraulaz.Swarm  Intelligence.  //  Oxford  University  Press,  1999.

4.Dorigo  M.,  V.  Maniezzo,  and  A.  Colorni.  The  antsystem:  Optimization  by  a  colony  of  cooperatingagents.  //  IEEE  Transactions  on  Systems,  Man  and  Cybernetics-Part  B,  26(1):29–41,  1996.