ОПТИМИЗАЦИЯ  КАЛИБРОВКИ  ИЗМЕРИТЕЛЬНЫХ  КАНАЛОВ

Пахоменков  Юрий  Михайлович

канд.  техн.  наук,  начальник  лаборатории  НПО  «Аврора»,  РФ,  г.  Санкт- Петербург

E-mail: 

CALIBRATION  OF  MEASURING  CHANNELS’  OPTIMIZATION

Yuriy  Pakhomenkov

candidate  of  Engineering  Sciences ,  Head  of  laboratory  SPA  “Avrora”,  Russia  Saint  Petersburg

АННОТАЦИЯ

Сформулирована  задача  оптимальной  цифровой  калибровки  измерительных  каналов  при  ограничении  разрядности  калибровочного  кода.  Получено  решение  двухмерной  задачи.  Описаны  результаты  моделирования  калибровки  измерительного  канала.

ABSTRACT

There  is  defined  a  problem  of  optimal  digital  calibration  of  measuring  channels  in  case  of  limiting  the  length  of  a  calibration  code.  The  solution  of  the  two-dimensional  problem  has  been  obtained.  The  simulation  data  of  a  measuring  channel’s  calibration  has  been  described. 

Ключевые  слова:  измерительные  преобразователи;  погрешность;  оптимизация;  нелинейное  программирование.

Keywords:  transducers;  error;  optimization;  nonlinear  programming.

В  состав  измерительных  каналов  (ИК)  входят  первичный  и  вторичный  преобразователи  (ПП  и  ВП),  а  также  линия  связи  (ЛС)  между  ними.  Каждая  из  этих  составных  частей  характеризуется  погрешностью  преобразования.  В  моноблочных  датчиках,  путем  регулирования  ВП,  удается  существенно  снизить  основную  составляющую  погрешности.  В  случаях  раздельного  размещения  ПП  и  ВП  индивидуальное  регулирование,  как  правило,  неприемлемо,  в  связи  с  требованием  взаимозаменяемости  составных  частей  ИК.  Компромисс  между  точностью  ИК  и  продолжительностью  замены  его  составных  частей  реализуют  с  помощью  оперативной  калибровки  ИК.  Известны  ВП,  включающие  сменные  элементы  с  характеристиками,  соответствующими  характеристикам  конкретных  ПП  и  ЛС  [2].  Изготовление,  и  хранение  таких  элементов,  с  учетом  вероятности  их  утраты,  удорожает  производство  и  эксплуатацию  систем.  Альтернативой  служит  применение  движковых  модульных  выключателей,  положения  движков  которых  отождествляют  с  разрядами  двоичного  кода.  Опыт  применения  таких  технических  решений  для  компенсации  аддитивных  погрешностей  [3,  4],  способствует  исследованиям  технических  решений  и  методик  коррекции  других  составляющих  погрешности  ИК.

Рисунок  1.  Номинальная  статическая  характеристика  ПП  (а),  отображение  полосы  погрешностей  на  плоскость  (б)

Погрешность  каждого  экземпляра  ПП  является  случайной  величиной,  поэтому  точки,  соответствующие  результатам  преобразования  принадлежат  «полосе  погрешностей»  ABCD  на  рис.1  а).  При  аддитивно-мультипликативном  характере  погрешности  ее  предельные  значения  описывают  выражением

,  (1)

где  ,  ,    —  текущее,  минимальное  и  максимальное  значение  преобразуемой  величины;

,    —  максимальные  по  абсолютной  величине  значения  аддитивной  и  мультипликативной  составляющих  погрешности.

Из  формулы  (1)  следует,  что  погрешность  ПП  при  любом  значении  измеряемой  величины  определяется  значениями  этой  погрешности  на  границах  диапазона  измерений,  а  ее  наибольшее  значение  составляет  .

Взаимно-однозначным  отображением  фигуры  ABCD  (рис.  1,  а)  на  плоскость  аддитивной  и  мультипликативной  составляющих  погрешности  является  прямоугольник  T1,  T3,  T5,  T7  (рис.  1  б),  каждая  точка  которого  соответствует  конкретному  экземпляру  ПП.  При  калибровке  ИК  континуальное  множество  точек  этого  прямоугольника  аппроксимируется  дискретным  множеством  узловых  точек  двумерной  сетки  с  шагами    и    по  координатам    и.  Тогда  остаточная  погрешность  преобразования  тождественная  «манхэттенскому»  расстоянию  от  изображающей  точки  до  ближайшего  узла  сетки,  по  абсолютной  величине  не  превышает  предельного  значения  ,  определяемого  выражениями

                                                                                          (2)

где  ,    —  разрядности  дискретизации  координат    и  соответственно.

При  ограничении  общей  разрядности  корректирующего  кода  некоторым  положительным  значением  ,  требование  наилучшей  аппроксимации  точек  прямоугольника  множеством  узлов  сетки  математически  формулируется  в  виде  задачи  нелинейного  программирования

                                                                                                              (3)

где  ,    —  аргументы  оптимизации.

Принимая  во  внимание  последующее  округление  результатов  оптимизации,  рассмотрим  решение  задачи  (3)  на  множестве  положительных  чисел. 

В  соответствии  с  методом  [4]  снимем  ограничения  неравенства  в  задаче  (3)  заменой  переменных  по  формулам  ,  ,  где  ,  —  переменные,  значения  которых  не  ограничены.  С  учетом  указанной  подстановки  задача  (3)  эквивалентна  минимизации  следующей  функции  Лагранжа

,  (4)

где  ,  ,    —  аргументы  оптимизации.

Стационарная  точка  функции  (4)  удовлетворяет  уравнениям

.

Оптимум  в  задаче  (3)  достигается  при  следующих  значениях  переменных

                                                                                                        (5)

Как  следует  из  выражений  (5),  оптимальной  является  сетка  с  квадратными  ячейками,  для  которых  .  На  практике  границы  полосы  погрешностей  известны  с  некоторой  погрешностью,  а  погрешности  оптимальных  значений  величин  (5)  могут  быть  оценены  по  формулам

где:  ,    —  относительные  погрешности  величин  ,  ;

,    —  отклонения  аргументов    и    от  оптимальных  значений;

,    —  абсолютная  и  относительная  погрешности  критерия.

С  целью  оценивания  погрешности,  обусловленной  округлением  переменных  до  целых  значений  в  формулах  (2)  выполнена  подстановка  в  качестве  аргументов  выражений  ;  .  С  помощью  разложения  в  степенной  ряд  по  переменной  ,  до  второго  порядка  включительно,  в  окрестности  оптимальных  значений  аргументов  получена  формула

,

где  ,  и    —  дискретность  и  относительная  величина  погрешности  критерия  соответственно. 

На  стадии  проектирования  ИК  по  известным  значениям  величин  ,  ,  их  погрешностям  и  заданной  величине  критерия,  пользуясь  формулами  (5,  6)  определяют  значения  переменных  ,    и  .

Методика  применения  полученных  выше  результатов  на  стадии  производства  составных  частей  ИК  различается  в  зависимости  от  соотношения  между  систематическими  и  случайными  составляющими  основной  погрешности  ПП.  Если  случайная  погрешность  пренебрежимо  мала,  то  по  результатам  измерения  выходных  сигналов  ПП  определяют  фактические  значения  его  основной  аддитивной  и  мультипликативной  погрешностей    и    соответственно.  Затем  рассчитывают  числовые  эквиваленты  калибровочных  кодов  по  формулам

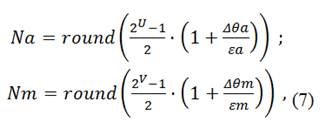
где:  ,    —  округленные  значения  числовых  эквивалентов  кодов  компенсации  аддитивной  и  мультипликативной  погрешностей;

  —  функция  округления  аргумента.

При  существенной  случайной  составляющей  погрешности  калибровка  ИК  выполняется  в  два  этапа.  На  первом  этапе  статистическими  методами  рассчитывают  оценочные  значения    и    систематических  погрешностей  ПП.  Затем  выполняют  расчёт  числовых  эквивалентов  калибровочных  кодов.

По  завершении  калибровки  осуществляют  проверку  метрологических  характеристик  ПП  с  учетом  корректирующих  воздействий,  и  с  применением  статистической  обработки  измеренных  значений.

Вычислительный  эксперимент  выполнен  в  соответствии  с  планом,  включающим  точки  T0…T8  (рис.  2  б).  При  этом  выходные  сигналы  модели  ИК  включали  аддитивную  и  мультипликативную  погрешность.  Моделирование  выполнялось  в  случаях  пренебрежимо  малой  и  существенной  случайной  составляющей  погрешности,  аддитивная  и  мультипликативная  составляющие  которой  распределены  по  нормальному  закону  с  математическим  ожиданием  0,1  и  дисперсией  0,033.  По  результатам  измерений  в  каждой  точке  плана  были  определены,  указанные  в  таблице,  числовые  эквиваленты  калибровочных  кодов  ,  ,  и  значения  остаточной  погрешности  .

Таблица  1. 

Результаты  моделирования  цифровой  калибровки

Как  следует  из  результатов  моделирования  методика  определения  кодов  калибровки  ИК  при  их  оптимальной  разрядности  позволила  существенно  снизить  систематическую  погрешность  ИК.  Описанный  метод  коррекции  систематических  составляющих  погрешности  ИК  реализуется  относительно  не  сложными  средствами  и  позволяет  обеспечить  компромисс  между  точностью  регулирования  и  продолжительностью  замены  отказавших  частей  ИК.

Список  литературы

1.Воробьев  Л.М.,  Воробьева  Т.М.  Нелинейные  преобразования  в  прикладных  вариационных  задачах.  М.:  «Энергия»,  1972.

2.Гришков  О.В.  и  др.  Измерительный  преобразователь  для  термопар  и  термометров  сопротивлений  Ш78,  Ш79  //  Приборы  и  системы  управления  №  11,  1986.

3.Патент  №  2190198,  МПК  G01К7/24,  09.04.2001,  опубл.  27.09.2002,  БИ  №  27.

4.Патент  №  2231760,  МПК  G01К7/16,  17.02.2003,  опубл.  27.06.2004,  БИ  №  18.