ЦИФРОВОЙ  ПРЕОБРАЗОВАТЕЛЬ  ГИЛЬБЕРТА  ШИРОКОПОЛОСНЫХ  СИГНАЛОВ

Здольников  Дмитрий  Викторович

аспирант  кафедры  акустики  и  звукотехники  Санкт-Петербургского  государственного  университета  кино  и  телевидения,  г.  Санкт-Петербург

E-mail:  d.zdolnikov@gmail.com

Уваров  Владимир  Константинович

д-р  тех.  наук,  проф.  кафедры  акустики  и  звукотехники  Санкт-Петербургского  государственного  университета  кино  и  телевидения,  г.  Санкт-Петербург

E-mail: 

DIGITAL  HILBERT  TRANSFORMER  OF  BROADBAND  SIGNALS

Dmitry  Zdolnoikov

postgraduate  student  of  department  of  acoustics  and  phonics  of  St.  Petersburg  State  University  of  Cinema  and  Television,  St.  Petersburg

Vladimir  Uvarov

doctor  of  Technical  Sciences,  Professor  of  St.  Petersburg  State  University  of  Cinema  and  Television,  St.  Petersburg

АННОТАЦИЯ

В  данной  статье  рассмотрен  цифровой  преобразователь  Гильберта  широкополосных  сигналов,  выполненный  на  базе  быстрого  преобразования  Фурье  (БПФ).  Приведены  семейства  кривых,  отражающие  влияние  количества  точек  БПФ  на  ширину  полосы  пропускания  и  величину  пульсаций  на  краях  частотных  характеристик  преобразователя.  Сделан  вывод  о  возможности  работы  данного  преобразователя  в  реальном  масштабе  времени.

ABSTRACT

In  this  article  a  digital  Hilbert  transformer  of  broadband  signals  realized  on  the  basis  of  the  fast  Fourier's  transform  (FFT)  is  considered.  The  families  of  curves  displaying  the  effect  of  number  of  points  in  the  FFT  on  width  of  pass-band  and  size  of  pulsations  at  edges  of  frequency  characteristics  of  these  transformer  are  presented.  A  conclusion  is  drawn  about  possibility  of  operation  of  this  transformer  in  real  time.

Ключевые  слова:  преобразование  Гильберта,  быстрое  преобразование  Фурье,  окно  Наттолла,  ширина  полосы  пропускания,  спад  амплитудно-чатотной  характеристики,  пульсации  фазоразностной  характеристики.

Keywords:  Hilbert  transform,  fast  Furier  transform,  Nuttall  window,  width  of  pass-band,  droop  of  amplitude  response,  ripple  of  phase-difference  response.

Согласно  теории  модуляций  [1]  любой  звуковой  сигнал    может  быть  представлен  в  виде  произведения  амплитудно-модулированной  S(t)  и  час­тотно-модули­рующей    его  функций:

                         (1)

где    —  опорный  сигнал,  определяемый  как  преобразование  Гильберта  исходного  сигнала:

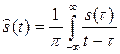                                            (2)

Формула  (2)  описывает  фазовый  сдвиг  между  сигналами    и  ,  который  равен  90^о.  В  технике  модуляционного  анализа-синтеза  это  преобразование  с  разной  степенью  точности  осуществляется  при  помощи  аналоговых  устройств  —  широкополосных  фазовращателей  [1,  c.  62].  Однако  сегодня,  в  век  развития  и  повсеместного  распространения  цифро­вых  технологий,  данная  реализация  не  актуальна.  Но,  не  смотря  на  это,  цифровых  устройств  модуляционного  анализа-синтеза  нет  до  сих  пор,  хотя  достигнутые  резуль­таты  представляют  большой  интерес  [2,  3,  6].  В  связи  с  этим  задачей  данного  исследования  является  разработка  цифрового  преобразователя  Гильберта,  способного  заменить  широкополосные  фазовращатели.

Цифровое  преобразование  Гильберта  может  быть  реализовано  как  во  временной  области  в  виде  цифровых  фильтров  Гильберта  [5,  7,  9],  так  и  в  частотной  —  через  дискретное  преобразование  Фурье  (метод  ДПФ)  [4,  8,  9].  При  широкополосных  входных  сигналах  более  подходящим  для  осуществления  цифрового  преобразования  Гильберта  является  метод  ДПФ,  обеспечиваю­щий  минимальные  пульсации  фазовой  характеристики  во  всей  полосе  пропус­кания  преобразователя  [9,  с.  380].  Согласно  методу  ДПФ,  вычисление  преобразования  Гильберта  осуществляется  через  спектр  аналитической  функции.  Алгоритм  расчета  преобразования  заключается  в  следующем  [8,  9].  Исходный  дискретный  сигнал    подвергается  N-точечному  ДПФ,  преобразуясь  в  дискретный  спектр  :

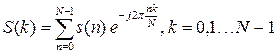,                             (3)

после  чего  вычисляется  Фурье-образ    аналитического  сигнала:

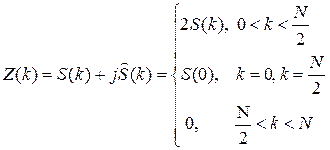,                   (4)

который  подвергается  N-точечному  обратному  ДПФ:

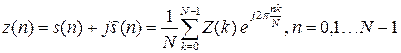,               (5)

результатом  которого  является  аналитическая  последовательность    во  временной  области,  мнимая    и  действительная    части  которой  связаны  между  собой  преобразованием  Гильберта. 

В  рамках  данной  работы  приведенный  алгоритм  был  доработан  и  реализован  в  среде  графического  моделирования  Labview.  Для  вычисления  ДПФ  использовался  алгоритм  быстрого  преобразования  Фурье  (БПФ)  по  смешанному  основанию  системы  счисления  (Cooley-Tykey  алгоритм)  [7,  с.  105].  Для  уменьшения  утечки  спектра,  непосредственно  перед  выполнением  БПФ  над  отсчетами  входного  сигнала,  находящимися  в  окне  анализа,  осуществлялась  операция  взвешивания  окном  Наттолла,  так  как  эта  оконная  функция,  согласно  [4,  с.  60],  обеспечивает  наименьший  уровень  боковых  лепестков  спектральных  составляющих  сигнала.  Понятно,  что  при  использовании  оконной  обработки,  значения  отсчетов  сигнала,  находящихся  в  окне  анализа,  искажаются,  что,  в  конечном  счете,  отражается  на  амплитуде  сигналов  на  выходе  преобразователя  Гильберта.  Для  того  чтобы  избежать  этого  в  [4,  с.  62]  предлагается  осуществлять  компенсацию  неравномерности  окна  Наттолла.  В  данной  работе  эта  проблема  решается  иначе.  При  каждой  итерации  из  последовательности    выделяется  лишь  один  комплексный  отсчет  с  номером  ,  мнимая    и  действительная    части  которого  являются  отсчетами  сопряженных  по  Гильберту  последовательностей,  получаемых  на  выходе  преобразователя.  Выделяемый  отсчет  является  центральным  и  не  искажается  окном  Наттолла.  Легко  понять,  что  получаемые  на  выходе  преобразователя  последовательности  будут  задержаны  на  m  отсчетов  относительно  входной  последовательности.

На  рисунке  1  изображены  амплитудно-частотная  (АЧХ)  и  фазоразностная  (ФРХ)  характеристики  реализованного  в  соответствии  с  приведенной  выше  методикой  преобразователя  Гилберта  при  N=50.  Судя  по  приведенным  характеристикам,  полученный  в  процессе  моделирования  преобразователь  имеет  довольно  широкую  полосу  пропускания,  в  которой  обеспечивается  относительное  постоянство  фазового  сдвига  и  амплитуды. 

a)  б)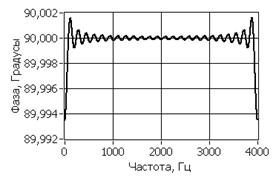 

Рисунок  1.  Частотные  характеристики  преобразователя  Гильберта  (N=50):  а)  АЧХ,  б)  ФРХ

Аналогичным  образом  функционирование  разработанного  преобразователя  Гильберта  было  исследовано  при  других  частотах  дискретизации  и  других  числах  точек  БПФ.  В  результате  были  получены  семейства  кривых,  отражающих  влияние  числа  точек  БПФ  на  ширину  полосы  пропускания  ΔF  (рис.  2)  и  на  отклонение  разности  фаз  выходных  сигналов  от  90^о  Ф  (рис.  3)  при  заданном  значении  D  (спада  АЧХ  на  краях  полосы  пропускания).

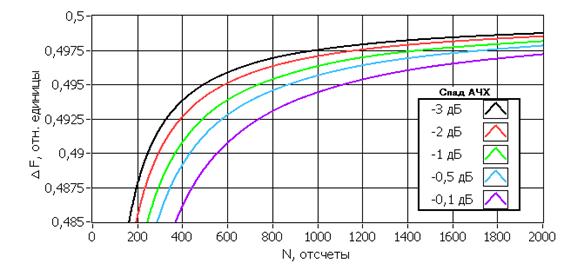
Рисунок  2.  Зависимость  ширины  полосы  пропускания  преобразователя  Гильберта  от  числа  точек  БПФ

По  приведенным  на  рисунке  2  кривым  можно  определить  зависимость  величины  получаемой  на  выходе  преобразователя  Гильберта  временной  задержки    от  нижней  граничной  частоты  полосы  пропускания  .  Величину  временной  задержки  можно  рассчитать  по  формуле:

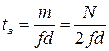,                                             (6)

где  fd  –  частота  дискретизации  входного  сигнала.  Судя  по  приведенным  на  рисунке  2  кривым,  если  задаться  каким-либо  фиксированным  значением  ,  то  при  подаче  на  вход  сигналов  с  разной  частотой  дискретизации,  для  поддержания  заданного  значения    необходимо  будет  менять  лишь  один  параметр  преобразователя  —  количество  точек  БПФ,  остальные  параметры  будут  оставаться  неизменными.  В  таблице  1  приведены  значения  временных  задержек  преобразователя  Гильберта,  рассчитанных  по  формуле  (6)  и  соответствующих,  согласно  кривым  на  рисунке  2,  различным  значениям  нижней  граничной  частоты  полосы  пропускания  .  Погрешность  измерения    составляет  примерно  0,5  мс.

Таблица  1.

Определение  задержки  выходных  сигналов  преобразователя  Гильберта

Известно  [4,  с.  16],  что  человеческий  слух  имеет  свойство  не  замечать  коротких  перерывов  в  звучании,  если  они  не  достигают  35  мс.  В  связи  с  этим,  на  основании  приведенных  в  таблице  1  данных,  можно  сделать  вывод  о  возможности  работы  рассматриваемого  преобразователя  Гильберта  в  режиме  реального  времени,  то  есть  в  режиме,  когда  запись  и  воспроизведение  звуковой  информации  может  осуществляться  одновременно,  без  заметных  на  слух  временных  задержек.  Как  видим,  наиболее  оптимальная  работа  преобразователя  в  реальном  времени,  в  сочетании  с  максимальной  шириной  полосы  пропускания,  обеспечивается  при  значении  нижней  граничной  частоты  полосы  пропускания  равной  50  Гц.  При  необходимости  это  значение  можно  уменьшить,  но  при  этом  возможны  потери  в  качестве  звучания.

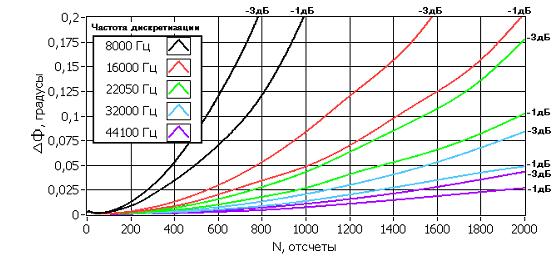
Рисунок  3.  Зависимость  ΔФ  от  числа  точек  БПФ  при  спадах  АЧХ  на  краях  полосы  пропускания  равных  1  дБ  и  3  дБ

На  рисунке  3  изображены  кривые,  полученные  при  значениях  спада  АЧХ  на  краях  полосы  пропускания  равных  –1  дБ  и  –3  дБ.  Кривые,  снятые  при  других  значениях  спада  АЧХ,  будут  иметь  такой  же  характер  и,  чтобы  не  загромождать  рисунок,  здесь  не  показаны.  Как  видим,  при  больших  значениях  частоты  дискретизации  входного  сигнала  величина  ΔФ  составляет  сотые  доли  градуса,  при  низких  частотах  дискретизации  ее  значение  значительно  больше  и  не  представляет  существенного  интереса.

Величина  ΔФ,  по  той  же  причине,  что  и    будет  оставаться  неизменной  при  изменении  частоты  дискретизации  входного  сигнала.  При  желании,  в  этом  можно  убедиться,  определив  по  кривым  на  рисунках  2  и  3  несколько  значений  ΔФ  при  разных  частотах  дискретизации  и  фиксированном  значении  .  Значения  ΔФ,  соответствующие  различным  значениям    и  D,  приведены  в  таблице  2.  Погрешность  измерения  ΔФ  составляет  примерно  ±0,005^о.

Таблица  2.

Определение  отклонения  разности  фаз  выходных  сигналов  от  90  градусов

Заключение

Согласно  [1],  широкополосные  фазовращатели,  применяемые  в  технике  модуляционного  анализа-синтеза,  должны  иметь  полосу  пропускания  от  20  до  20000  Гц;  прямолинейную,  равную  единице  во  всей  полосе  пропускания  АЧХ,  и  величину  отклонения  фазовой  характеристики  от  90^о  ΔФ=0,1^о.  При  сравнении  этих  параметров  с  параметрами  приведенными  в  таблицах  1  и  2,  можно  сделать  вывод  о  возможности  частичной  замены  широкополосных  фазовращателей  на  рассмотренные  в  данной  работе  цифровые  преобразователи  Гильберта  с  полосой  пропускания  от  50  до  22000  Гц.  В  частотности,  данная  замена  будет  актуальной  в  устройствах  обработки  речевых  сигналов,  спектр  которых  практически  не  содержит  частотных  составляющих  в  области  ниже  50  Гц.

Помимо  техники  модуляционного  анализа-синтеза,  данный  преобразователь  можно  использовать  также  и  в  других  областях  науки  и  техники,  где  есть  необходимость  в  квадратурной  обработке  широкополосных  сигналов.  Приведенные  исследования  могут  быть  продолжены  с  целью  усовершенствования  приведенной  методики  и  увеличения  полосы  пропускания  преобразователя  Гильберта,  пригодной  для  его  работы  в  реальном  времени.

Список  литературы:

1.Ишуткин  Ю.М.,  Уваров  В.К.  Основы  модуляционных  преобразований  звуковых  сигналов.  /  Под  ред.  В.К.  Уварова  СПб.:  СПбГУКиТ,  2004.  —  102  с. 

2.Китанов  М.Ю.  Разработка  метода  и  технических  средств  автоматического  изменения  времени  послезвучия  с  целью  повышения  разборчивости  речи:  Афтореф.  дис.  канд.  тех.  наук.  СПб.,  2011.  —  24  с.

3.Маркин  Д.Н.  Разработка  метода  и  технических  средств  компандирования  спектров  речевых  сигналов:  Автореф.  дис.  канд.  тех.  наук.  СПб.,  2008.  —  22  с.

4.Попов  О.Б.,  Рихтер  С.Г.  Цифровая  обработка  сигналов  в  трактах  звукового  вещания:  учеб.  для  вузов.  М.:  Грячая  линяя  Телеком,  2007.  —  341  с.

5.Солонина  А.И.  Основы  цифровой  обработки  сигналов  //  А.И.  Солонина,  Д.А.  Улахович,  С.М.  Арбузов,  Е.Б.  Соловьева:  курс  лекций,  изд.  2-е  испр.  и  перераб.  СПб.:  БХВ-Петербург,  2005.  —  768  с.

6.Уваров  В.К  Точное  компандирование  частотного  и  динамического  диапазонов  звуковых  сигналов.  СПб.:  СПбГУКиТ,  2001.  —  326  с. 

7.Федосов  В.П.,  Нестеренко  А.К.  Цифровая  обработка  сигналов  в  LabVIEW  /  под  ред.  В.П.  Федосова.  М.:  ДМК  Пресс,  2007.  —  472  с.

8.Хованова  Н.А.,  Хованов  И.А.  Методы  анализа  временных  рядов.  Саратов:  Изд-во  ГосУНЦ  КОЛЛЕДЖ.  2001.  —  120  с.

9.Lyons  Richard  G.  Understanding  digital  signal  processing.  2nd  ed.  New  Jersey:  Prentice  Hall,  2004.  —  688  p.