РЕШЕНИЕ  КОНТАКТНЫХ  ЗАДАЧ  ТЕОРИИ  УПРУГОСТИ  С  ПОМОЩЬЮ  АЛЬТЕРНИРУЮЩЕГО  МЕТОДА  ШВАРЦА

Яковлев  Максим  Евгеньевич

аспирант,  ассистент  кафедры  ФН-2,  МГТУ  им.  Н.Э.  Баумана,  г.  Москва

E-mail:  me-yakovlev@rambler.ru

SOLUTION  OF  CONTACT  PROBLEM  OF  ELASTICITY  BY  SCHWARZ  ALTERNATING  METHOD

Maxim  Yakovlev

graduate  student,  assistant,  Moscow  State  Technical  University,  Moscow

Аннотация

В  работе  рассмотрены  особенности  алгоритма  численного  решения  контактных  задач  механики  деформируемого  твёрдого  тела  в  сложных  двухмерных  областях.  Решение  построено  в  рамках  конечно-элементной  технологии  на  основе  альтернирующего  метода  Шварца.  Метод  состоит  в  попеременном  выполнении  на  контактной  поверхности  силовых  и  кинематических  граничных  условий.  Проведён  анализ  напряжённо-деформированного  состояния  замкового  соединения.

ABSTRACT

The  paper  discusses  the  features  of  the  algorithm  of  numerical  solution  of  contact  problems  of  solid  mechanics  in  complex  two-dimensional  fields.  The  solution  is  constructed  in  the  framework  of  finite  element  technology  based  on  the  Schwarz  alternating  method.  The  method  consists  of  alternating  between  fulfilling  the  power  and  the  kinematical  boundary  conditions  on  the  contact  surface.  The  stress-strain  state  of  the  tool  joint  is  analyzed.

Ключевые  слова:  контактное  взаимодействие  упругих  тел,  метод  Шварца,  метод  конечных  элементов,  итерационное  решение

Keywords:  Contact  interaction  of  elastic  bodies,  the  Schwartz  method,  finite  element  method,  the  iterative  solution

Оценке  надёжности  и  долговечности  ответственных  элементов  конструкций  предшествует  анализ  напряжённо-деформированного  состояния  с  учетом  особенностей  контактного  взаимодействия.  Поскольку  контакт  —  это  основной  метод  приложения  нагрузок  к  деформируемому  телу,  решение  контактных  задач  является  весьма  важным  и  актуальным.  Аналитические  решения  могут  быть  получены  только  для  очень  ограниченного  класса  задач  механики  деформируемого  твердого  тела,  поэтому  необходимым  является  дальнейшее  развитие  прикладных  методов  математического  моделирования  применительно  к  решению  контактных  задач  механики  с  учетом  неупругого  деформирования  материала  исследуемых  конструкций. 

Актуальной  является  также  проблема  создания  новых  эффективных  алгоритмов  и  на  их  основе  современного  прикладного  программного  обеспечения  для  решения  контактных  задач  вычислительной  механики.  Ниже  рассматривается  алгоритм  решения  контактной  задачи  теории  упругости,  базирующийся  на  альтернирующем  методе  Шварца.

Математическая  формулировка  контактной  задачи  теории  упругости  включает:  уравнения  равновесия

  ;         (1)

граничные  условия

;               (2)

  ;           (3)

соотношения  Коши

;  (4)

и  определяющие  уравнения  в  форме  закона  Гука

                   (5)

здесь  D  —  матрица  Гука,    —  вектор  напряжений,    —  вектор  деформации,    —  вектор  заданных  перемещений  точек  поверхностей    и  ,    —  компоненты  распределенной  нагрузки    на  поверхностях    и  .

Кроме  того,  на  поверхности  контакта    должны  быть  выполнены  условия  контактного  взаимодействия:  кинематическое

                               (6)

и  силовое

,                                            (7)

где:  ,    —  проекции  перемещений  граничных  точек  на  внешнюю  нормаль  к  границе  тела  B; 

  —  начальное  расстояние  по  нормали  между  граничными  точками; 

,    —  составляющие  поверхностных  сил  по  внешней  нормали  к  границе  тела  B.  Соотношения  (6)  и  (7)  соответствуют  случаю,  когда  трение  не  учитывается.

Для  решения  контактной  задачи  (1)—(7)  был  использован  алгоритм,  основанный  на  альтернирующем  методе  Шварца  [3—5].  Данный  метод  является  итерационным.  Его  суть  состоит  в  следующем.  В  первом  шаге  на  контактных  поверхностях  тел    и    соответственно    и    задают  начальные  перемещения    и  ,  которые  имеют  смысл  дополнительных  кинематических  условий. 

Далее  решают  независимо  две  подобные  задачи  теории  упругости  для  тел    и  .  Затем  вычисляют  поверхностные  силы    и    на  контактных  поверхностях    и    и  корректируют  их  так,  чтобы  выполнялись  силовые  контактные  условия  (7). 

Во  втором  шаге  на  контактных  поверхностях    и    задают  силовые  контактные  условия,  в  качестве  которых  используют  скорректированные  поверхностные  силы    и  ,  и  вновь  решают  независимо  задачи  теории  упругости  отдельно  для  тел    и  .  По  результатам  полученных  решений,  выполняют  коррекцию  компонент  векторов  перемещений    и    соответственно  точек  контактных  поверхностей    и    с  тем,  чтобы  выполнялись  кинематические  условия  контактного  взаимодействия  (6).  Скорректированные  перемещения  точек  контактных  поверхностей    и    рассматривают  в  качестве  новых  кинематических  граничных  условий  на  геометрически  измененных  поверхностях  контакта    и    и  вновь  решают  независимо  задачи  теории  упругости  отдельно  для  тел    и  . 

Для  численного  решения  контактной  задачи  был  использован  метод  конечных  элементов  [1].  Рассмотрим  контакт  двух  тел    и  .  Пронумеруем  узлы  контактных  поверхностей    и    и  введем  в  рассмотрение  векторы  —    и  ,  ,  первый  из  которых  составлен  из  компонент  перемещений    и    узлов,  расположенных  на  контактной  поверхности  ,  а  второй  —  из  компонент    и    узловых  сил  тех  же  узлов.  Последовательно  для  каждого  тела  в  соответствии  с  алгоритмом  выполняется  коррекция  компонент  векторов    и  ,  .  Коррекция  компонентов  векторов    и  ,    реализуется  поочередно:  на  каждой  четной  итерации  корректируются  компоненты  вектора  ,  а  на  нечетной  итерации  –  .

Коррекция  компонент  вектора    выполняется  в  соответствии  с  соотношением

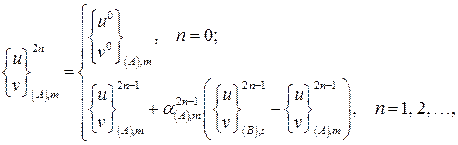  (8)

где:    —  итерационный  параметр, 

    —  узел,  лежащий  на  контактной  поверхности    тела  , 

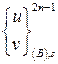  —  вектор  перемещений  сходственной  точки  ,  лежащей  на  контактной  поверхности    тела  .

Для  коррекции  компонент  вектора  контактных  узловых  сил    используется  формула 

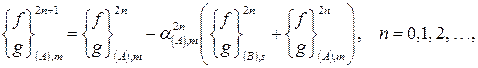  (9)

здесь    —  итерационный  параметр,      —  узел,  лежащий  на  контактной  поверхности    тела  ,  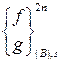  —  вектор  контактных  узловых  сил  сходственной  точки  ,  лежащей  на  контактной  поверхности    тела  .

Пусть  для  определенности    и  .  На  четных  итерациях  и  нечетных  итерациях  итерационные  параметры    и    соответственно  определяются  с  помощью  выражений

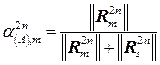,    (10)

где:    —  норма  вектора  перемещения    узла    ,  лежащего  на  контактной  поверхности    тела  , 

  —  норма  вектора  перемещения    сходственной  точки  ,  лежащей  на  контактной  поверхности    тела  , 

  —  норма  вектора  контактных  сил    узла  , 

  —  норма  вектора  контактных  сил    сходственной  точки    [4].

Описанный  выше  алгоритм  был  использован  для  расчета  НДС  замковых  соединений  типа  “ласточкин  хвост”  лопаток  и  дисков  компрессора.  Изучалось  распределение  напряжений  в  наиболее  напряженной  области  соединений  —  пазах  дисков.  Геометрические  параметры  соединения  взяты  из  работы  [2].  В  силу  симметрии  для  всех  деталей  рассматривается  правая  половина.

Предполагалось,  что  нагрузка  на  лопатку  моделируется  приложением  к  верхней  грани  верхнего  тела  растягивающей  распределенной  нагрузки  МПа.  На  рис.  1  показано  распределение  напряжений,  действующих  в  направлении  растягивающей  нагрузки.

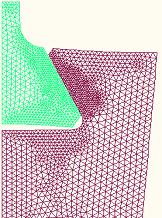
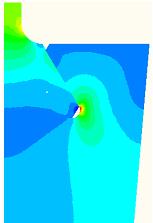
Рисунок  1.  Распределение  компоненты  тензора  напряжения    (МПа)

Выводы:

Разработан  алгоритм  решения  контактной  задачи  с  учетом  упругопластической  деформации,  основанный  на  альтернирующем  методе  Шварца.  Проведено  исследование  НДС  замкового  соединения  типа  «ласточкин  хвост»  диска  и  лопатки  компрессора  с  учетом  контактного  взаимодействия.

Список  литературы:

1.Зенкевич  О.  Метод  конечных  элементов  в  технике.  М.:  Мир,  1975.  —  542  с.

2.Мавлютов  Р.Р.  Концентрация  напряжений  в  элементах  конструкций.  М.:  Наука,  1996.  —  240  с.

3.Можаровский  Н.С.,  Качаловская  Н.Е.  Приложение  методов  теории  пластичности  и  ползучести  к  решению  инженерных  задач  машиностроения:  В  2  т.  Т.  2:  Методы  и  алгоритмы  решения  краевых  задач.  К.:  Выща  школа,  1991.  —  287  с.

4.Станкевич  И.В.,  Яковлев  М.Е.,  Си  Ту  Хтет.  Разработка  алгоритма  контактного  взаимодействия  на  основе  альтернирующего  метода  Шварца  //  Вестник  МГТУ  им.  Н.Э.  Баумана.  Сер.  Естественные  науки.  —  2011.  —  Спец.  вып.  Прикладная  математика.  —  С.  134—141.

5.Цвик  Л.Б.  Принцип  поочередности  в  задачах  о  сопряжении  и  контакте  твердых  деформируемых  тел.  //  Прикл.  Мех.  —  1980  —  т.  16,  Ш  I  —  С.  13—18.