Статья опубликована в рамках: XXVII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 30 октября 2013 г.)
Наука: Технические науки
Секция: Машиностроение и машиноведение
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ ПЕРЕДНЕПРИВОДНОГО АВТОМОБИЛЯ В РЕЖИМЕ СТАЦИОНАРНОГО ПОВОРОТА
Копылов Семен Юрьевич
аспирант кафедры «Автомобилестроение», филиала Южно-Уральского государственного университета (НИУ), в городе Миассе
E-mail: samens@mail.ru
Трояновская Ирина Павловна
профессор, д-р техн. наук, профессор кафедры «Колёсные, гусеничные машины и автомобили», Южно-Уральского государственного университета (НИУ), г. Челябинск
E-mail:
MATHEMATICAL MODEL OF MOTION FRONT WHEEL DRIVE CAR MODE FIXED ROTATION
Semen Kopylov
graduate student of automobile production department, branch of South Ural State University (NR), Miass
Irina Troyanovskaya
professor, Doctor of Technical Sciences, professor of "Wheel, tracked vehicles and cars" departments, South Ural State University (NR), Chelyabinsk
АННОТАЦИЯ
Цель: построение математической модели движения переднеприводного автомобиля в режиме стационарного поворота на основе математической теории трения. Результат расчёта: параметры поворота автомобиля через неизвестные координаты мгновенных центров скольжения (МЦС) опорных площадок колес. Вывод: применение данного метода позволяет оценить влияние конструктивных параметров автомобиля, его схемы управления на характеристики криволинейного движения.
ABSTRACT
Purpose: to construct a mathematical model of the motion front wheel drive car in a stationary mode, turn on the mathematical theory of friction. The result of the calculation: the parameters of the car turn through the unknown coordinates of instantaneous centers of sliding , the bearing surfaces of the wheels. Conclusion: The application of this method to evaluate the influence of design parameters of the vehicle and its control scheme on the performance of curvilinear motion.
Ключевые слова: модель движения, стационарный поворот, переднеприводный автомобиль, центры скольжения.
Keywords: motion model, a fixed rotation, front-drive car, the centers of sliding.
Для изучения движения автомобиля на повороте чаще всего используются модели на основе теории бокового увода [6]. Эти модели нашли широкое применение при описании машин с межколесными дифференциалами, движущимися практически без скольжения колес.
Однако, для учета скольжения колес по грунту предлагается применить методику моделирования криволинейного движения тракторных агрегатов, где любое транспортное средство (ТС) рассматривается как управляемый объект, криволинейное движение которого определяется наложенными на него связями, обеспечиваемыми конструкцией и системой управления [5].
С грунтом ТС (автомобиль) взаимодействует посредством плоских площадок, число которых равно числу колес (4 пятна контакта). В каждом контакте возникают силы и момент трения (![]() ,
,![]() ), являющиеся функциями координат (
), являющиеся функциями координат (![]() ) мгновенных центров скольжения (МЦС) [3]:
) мгновенных центров скольжения (МЦС) [3]:
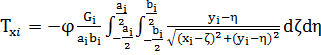 (1)
(1)
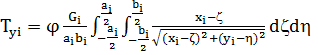 (2)
(2)
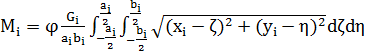 (3)
(3)
где: Gi — вес, приходящийся на i колесо, кг;
![]() — коэффициент сцепления колеса с дорогой;
— коэффициент сцепления колеса с дорогой;
ai ,bi — длина и ширина пятна контакта i колеса, соответственно, мм.
Ширина колеса (bi) практически не меняется с нагрузкой (Gi) [1], поэтому ее берём из стандартного обозначения шины. Длину следа можно рассчитать по теореме Пифагора:
![]() (4)
(4)
где: ![]() — свободный радиус i колеса, мм;
— свободный радиус i колеса, мм;
![]() — динамический радиус i колеса (с учётом прогиба hi), мм.
— динамический радиус i колеса (с учётом прогиба hi), мм.
Поскольку прогиб колеса зависит от его конструктивных параметров (bi, Di), внутреннего давления в шине (r) и вертикальной нагрузки на колесо(Gi):
![]() (5)
(5)
где: ![]() — среднее давление в шине, КПа;
— среднее давление в шине, КПа;
bi — ширина i колеса, мм;
Di — внешний диаметр i колеса, мм,
то подставив значения радиусов и прогиба в формулу (4) получаем следующее выражение длины следа:
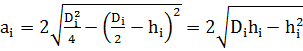 (6)
(6)
Для позиционирования МЦС введем следующие системы координат:
· общая система для всего ТС, с началом в центре поворота (![]() — координаты заднего внутреннего колеса в общей системе);
— координаты заднего внутреннего колеса в общей системе);
· четыре местные системы для каждой опорной площадки, с началом координат в геометрическом центре следа (![]() - координаты МЦС в местных системах координат).
- координаты МЦС в местных системах координат).
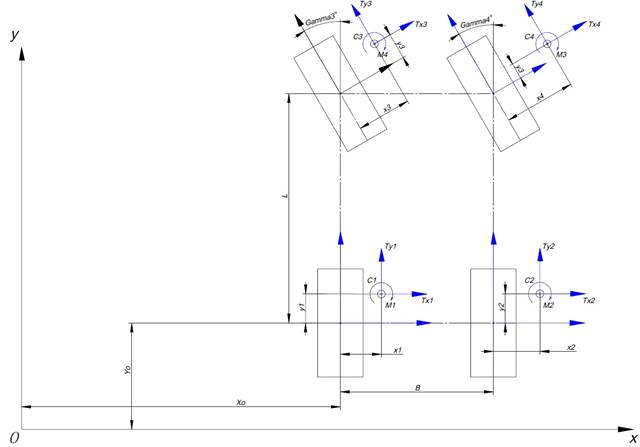
Рисунок 1. Расчётная схема поворота ТС
Запишем координаты МЦС всех колес в общей системе координат, связав тем самым общую и местные системы координат (рисунок 1):
![]() х1,
х1, ![]() 1, (7)
1, (7)
![]() х2 ,
х2 , ![]() 2, (8)
2, (8)
![]() ,
, ![]() , (9)
, (9)
![]() ,
, ![]() , (10)
, (10)
где: B, L — колея и продольная база, соответственно;
g3, g4 — углы поворота передних управляемых колес относительно корпуса.
Составим систему уравнений криволинейного движения произвольного ТС.
Три уравнения движения для стационарного поворота (криволинейного движения с постоянной угловой скоростью и радиусом поворота) имеют вид [5]:
![]()
(11)
![]()
(12)
![]()
(13)
где: m — масса ТС, кг;
w — угловая скорость движения ТС.
При вращательном движении скорость любой точки корпуса перпендикулярна радиус-вектору, опущенному из центра поворота машины [4]. Поскольку в МЦС скольжение отсутствует, то скорость корпуса над этой точкой равна теоретической скорости, которая направлена всегда вдоль плоскости вращения колеса. На основе этого можно записать уравнения геометрических связей, отражающих то, что МЦС площадок контакта колес лежат на перпендикулярах, опущенных из центра поворота на плоскости вращения колес [2]:
![]() (14)
(14)
![]() , (15)
, (15)
Для задних колес (углы поворота относительно корпуса равны нулю):
![]() (16)
(16)
![]() (17)
(17)
Еще три уравнения кинематических связей описывают взаимодействие узлов трансмиссии и рулевого управления. Так для переднеприводного автомобиля наличие межколесного дифференциала на передней оси характеризует равенство крутящих моментов, что при равных радиусах колес соответствует равенству тяговых усилий:
![]() (18)
(18)
Поскольку задние колеса являются ведомыми, то на них отсутствуют тяговые усилия, что можно записать в виде:
![]() (19)
(19)
![]() (20)
(20)
С учетом выражений (1—3) уравнения (18—19) приобретают вид [КД]:
![]() и
и ![]()
В случае дополнительного торможения задним внутренним колесом уравнение (18) заменяется на (при полном торможении МЦС колеса совпадает с центром поворота всей машины):
![]() (21)
(21)
В результате решения системы уравнений 10 уравнений (11—20) с учетом выражений силовых факторов (1—3) и преобразования координат (7-10) получим неизвестные координаты МЦС всех колес (х1, у1, х2, у2, х3, у3, х4, у4) и центра поворота (х0, у0). Используя эти значения можно найти все основные параметры поворота:
1. Силы и моменты действующие в пятне контакта (формулы 1—3),
2. Буксование каждого колеса
![]() (22)
(22)
3. Радиус поворота ТС по наиболее удаленному колесу:
![]() (23)
(23)
Возможность отражать схему управления путем замены уравнений связи позволяет проводить сравнительный анализ машин с различными типами трансмиссий. Использование уравнений преобразования (7—10) позволяет отслеживать влияние конструктивных параметров на характеристики криволинейного движения машины. В следующей статье автор приведёт пример расчёта криволинейного движения ТС в режиме стационарного поворота с заторможенным задним внутренним колесом. Изучение такого движения даёт возможность контролируемого применения тормозных усилий на колесах с целью увеличения манёвренности автомобиля.
Список литературы:
1.Мицын Г.П. Стационарный поворот минитрактора (экспериментальные результаты) / Г.П. Мицын и др. / Сборник научных трудов МАДИ (ТУ): Проблемы проектировании, строительства и эксплуатации автомобильных дорог, М.: МАДИ, 2001, — с. 233—237.
2.Позин Б.М. Кинематические соотношения при взаимодействии движителя с грунтом при повороте / Б.М. Позин, И.П. Трояновская / Вестник ЮУрГУ, серия машиностроение, вып. 7, № 14(54), Челябинск: ЮУрГУ. 2005 — с. 93—96.
3.Тарг С.М. Краткий курс теоретической механики / С.М. Тарг / М.: Высшая школа, 1986. — 416 с.
4.Трояновская И.П. Взаимодействие колесного движителя с грунтом на повороте с точки зрения механики / И.П Трояновская / Тракторы и сельскохозяйственные машины, — № 3, — 2011, — с. 29—35.
5.Трояновская И.П. Методология моделирования криволинейного движения тракторных агрегатов: дисс. … доктора технических наук / И.П. Трояновская / Челябинск: ЮУрГУ, 2011. — 296 с.
6.Фаробин Я.Е. Теория поворота транспортных машин / Я.Е. Фаробин / М.: Машиностроение, 1970. — 176 с.
дипломов


Комментарии (1)
Оставить комментарий