Статья опубликована в рамках: XX Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 17 апреля 2013 г.)
Наука: Технические науки
Секция: Безопасность жизнедеятельности человека, промышленная безопасность, охрана труда и экология
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА РАСПРОСТРАНЕНИЯ В АТМОСФЕРЕ ГАЗОВЫХ ЗАГРЯЗНИТЕЛЕЙ ПРИ РАЗЛИЧНЫХ ПОГОДНЫХ УСЛОВИЯХ
Чернявский Сергей Анатольевич
аспирант НИУ МИЭТ, г. Зеленоград
E-mail: spin204@yandex.ru
MATHEMATICAL MODEL OF PROCESS OF DISTRIBUTION OF GAS POLLUTANTS IN THE ATMOSPHERE UNDER DIFFERENT WEATHER CONDITIONS
Sergey Chernyavskiy
Postgraduate of National Research University of Electronic Technology, Zelenograd
АННОТАЦИЯ
В работе проведены аналитические исследования процессов распространения в атмосфере вредных выбросов предприятий. В качестве основного атмосферного загрязнителя рассматривается углекислый газ (CO2).
В работе приводится функция Грина для задачи о разовом мгновенном выбросе вредной примеси в стандартном приземном слое атмосферы с заданным ветровым полем и получено выражение для концентрации примесей в стационарном случае и при непрерывно действующем источнике загрязнения. Построены уровни равного загрязнения атмосферы и проанализирована их трансформация при изменении параметров источника.
ABSTRACT
In the work we are conducted analytical research of the processes of propagation in atmosphere of harmful emissions of the enterprises. As the main atmospheric pollutant is considered carbon dioxide (CO2).
The work gives the Green's function for the problem of a one-time instantaneous release of harmful impurities in the standard surface layer of the atmosphere with a given wind field and the obtained expression for the concentration of impurities in the stationary case, and the continuously active source of pollution. We are built levels equal to the pollution of the atmosphere and analyzed their transformation to change the settings of the source.
Ключевые слова: турбулентная диффузия; стационарный источник; газовый загрязнитель; абсорбция.
Keywords: eddy diffusion; stationary source; gas pollutant; absorption.
Газообразные вещества, выбрасываемые в атмосферу функционирующими предприятиями, представляют серьёзную угрозу для стабильности атмосферы и климата. Например, накопление парниковых газов нарушает естественный температурный баланс, ведет к потеплению поверхности Земли и, как следствие, глобальному изменению климата. Другие газы, такие, как аммиак, оксиды азота и серы приводят к химическому загрязнению атмосферы, кислотным дождям и фотохимическому смогу. Работы, посвящённые исследованию загрязнения атмосферы, ведутся уже много лет и сохраняют свою актуальность.

Рисунок 1. Распространение газовых загрязнителей в атмосфере и воздействие на них атмосферных осадков
Современные математические и компьютерные методы расчётов концентраций газовых загрязнителей в атмосфере позволяют точнее предсказывать загрязнение атмосферы и, в частности, более детально изучать их воздействие на климат Земли.
Рассматривается задача о распространение в приземном слое атмосферы газовых загрязнителей, выбрасываемых промышленным предприятием. Относительно источника выбросов экологического загрязнения, моделируемого точечным источником, будем считать известными его «производительность» — ![]() и его пространственное расположение. Ветровое поле
и его пространственное расположение. Ветровое поле ![]() будем считать плоскослоистым, постоянным на каждой высоте и не меняющемся во времени.
будем считать плоскослоистым, постоянным на каждой высоте и не меняющемся во времени.
В задаче требуется определить распределение концентрации газов в атмосфере.
В основу математической модели положена Гауссова модель. Основным уравнением, характеризующим распространение газов в атмосфере, является локальный закон сохранения вещества, который представлен в виде:
![]() (1)
(1)
Здесь ![]() — концентрация газового загрязнителя;
— концентрация газового загрязнителя;
![]() — коэффициент, описывающий уменьшение концентрации газового загрязнителя за счёт абсорбции;
— коэффициент, описывающий уменьшение концентрации газового загрязнителя за счёт абсорбции;
![]() — плотность потока диффундирующего вещества, представляющего собой сумму потоков диффузии:
— плотность потока диффундирующего вещества, представляющего собой сумму потоков диффузии:
![]() , (2)
, (2)
![]() , (3)
, (3)
![]() (4)
(4)
![]() — поток молекулярной диффузии;
— поток молекулярной диффузии;
![]() — поток турбулентной диффузии;
— поток турбулентной диффузии;
![]() — коэффициент молекулярной диффузии, который отражает перенос газа в нижний слой атмосферы;
— коэффициент молекулярной диффузии, который отражает перенос газа в нижний слой атмосферы;
![]() — коэффициент турбулентной диффузии, который отражает перенос газа в верхние слои атмосферы в случае анизотропной среды.
— коэффициент турбулентной диффузии, который отражает перенос газа в верхние слои атмосферы в случае анизотропной среды.
Перенос газового загрязнителя в нижний слой незначителен в отличие от переноса в верхние слои атмосферы, поэтому ![]() .
.
С учётом подстановок в уравнение (1) соотношений (2)—(4) и сделанных математических преобразований имеем следующее дифференциальное уравнение [1]:
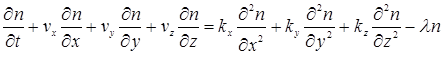 (5)
(5)
Уравнение (5) представляет собой уравнение турбулентной диффузии. Его решение получим при следующих приближениях.
Ветровое поле стационарно, вектор ![]() параллелен поверхности земли и направлен вдоль оси x, в выбранной нами системе координат. На первом этапе будем полагать, что осадки отсутствуют
параллелен поверхности земли и направлен вдоль оси x, в выбранной нами системе координат. На первом этапе будем полагать, что осадки отсутствуют ![]() . Относительно турбулентности атмосферы, предположим её изотропность и однородность, т. е.
. Относительно турбулентности атмосферы, предположим её изотропность и однородность, т. е. ![]() .
.
Смоделируем источник экологического загрязнения точечным источником мощности M, расположенного в точке с координатами ![]() , через которую в атмосферу выбрасывается газовый загрязнитель [2], [3].
, через которую в атмосферу выбрасывается газовый загрязнитель [2], [3].
С учётом сделанных допущений уравнение (5), описывающее появление и распространение парниковых газов, имеет вид:
 (6)
(6)
Естественно предположить, что на бесконечном удалении от источника, концентрация выброшенных парниковых газов стремится к нулю, т. е. n → 0 при ![]() .
.
Решения уравнения (6), описывающего эволюцию распространения парникового газа при разовом выбросе имеют вид [4]:
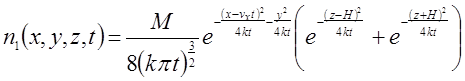 (7)
(7)
 (8)
(8)
где: t — время, прошедшее после выброса, с;
M — мощность непрерывного точечного источника (выбросы вещества в единицу времени), г/с;
k — коэффициент турбулентной диффузии, м2/с;
vx — средняя по высоте скорость ветра, м/с;
H — высота трубы, м.
Решение (7) имеет место при распространении газового загрязнителя над земной, а (8) — над водной поверхностями.
В основу (7) и (8) входит функция Грина для одномерного случая распространения газов в атмосфере, которая представлена формулой:

График функции Грина представлен на рисунке 2.

Рисунок 2. График функции Грина для уравнения турбулентной диффузии в одном измерении для единичного источника, введённого при ![]() ,
, ![]() для различных моментов времени
для различных моментов времени
Для исследования процесса распространения концентрации CO2 зададим числовые параметры (7) и (8):
![]()
Для уравнений (7) и (8) составим таблицу уравнений окружностей при заданном времени для иллюстрации распространения CO2 в атмосфере, также численно зададим значения функции распространения концентрации ![]() и
и ![]() в соответствующие моменты времени.
в соответствующие моменты времени.
Таблица 1.
Численные значения функций распространений концентраций над земной и водной поверхностями в соответствующий момент времени, и уравнения, определяющие линии уровня распространения газового загрязнителя
|
Время (ti, с) |
Значение функции |
Значение функции |
Уравнение |
|
6 |
1,841·10-8 |
3,96·10-12 |
|
|
24 |
2,302·10-9 |
1,237·10-13 |
|
|
54 |
6,821·10-10 |
1,63·10-14 |
|
|
96 |
2,877·10-10 |
3,868·10-15 |
|
|
150 |
1,473·10-10 |
1,267·10-15 |
|
По таблице 1 построен график распространения концентрации газа над подстилающей поверхностью. По структуре график распространения концентрации CO2 над земной поверхностью подобен график распространения концентрации CO2 над водной поверхностью. Численно различаются только значения ![]() и
и ![]() .
.
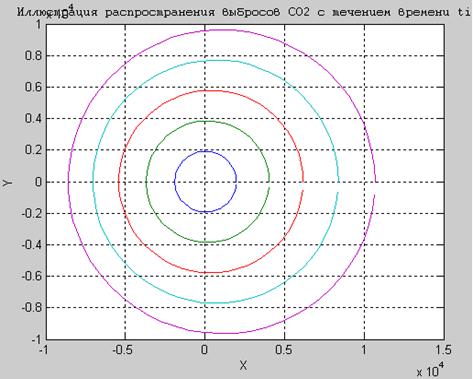
Рисунок 3. Распространение выбросов СО2 в атмосфере при разных значениях функции (28) и (29) в разные моменты времени
Таблица 1 и рисунок 3 подтверждают факт естественных условий, согласно которым с большим течением времени концентрация CO2 уменьшается.
Проанализировав (8) очевидно, что водная поверхность хорошо абсорбирует газовый загрязнитель, т. е. [1]:

В частности, водная поверхность, особенно холодная вода, хорошо поглощает СО2.
В случае непрерывного действия источников, функцию стационарного распределения концентрации газовых загрязнителей в атмосфере можно получить, используя соотношения (7) или (8).
В качестве примера, рассмотрим вывод выражения для стационарной концентрации газового загрязнителя над земной поверхностью.
Нетрудно видеть, что:
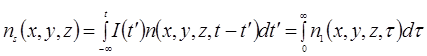
Значение интеграла дающего функцию распределения концентрации газового загрязнителя для случая стационарных выбросов при отсутствии атмосферных осадков, имеет вид:
 (9)
(9)
При наличии атмосферных осадков в нестационарном случае при разовом выбросе, функция распространения концентрации газового загрязнителя может быть представлена в виде:
![]() ,
,

Соответствующее стационарное решение nλ в случае атмосферных осадков находится по формуле, аналогичной (9):
 (10)
(10)
Коэффициент абсорбции λ зависит от интенсивности осадков, и влияет на уменьшение газовых загрязнителей из атмосферы. В работе в качестве примера осадков взята морось, воздействующая на газовый загрязнитель, интенсивность которой 0,01 с-1.
Контурные графики, иллюстрирующие распространение газа в пространстве при отсутствии и наличие атмосферных осадков подобны. Структура рисунка начинает изменяться при очень сильной скорости ветра, т.е. при мощном урагане.

Рисунок 4. Контурный график распространения CO2 в атмосфере
В формуле (10) присутствует дополнительный сомножитель, отвечающий за воздействие атмосферных осадков на газовый загрязнитель. Данный сомножитель называется эффективным коэффициентом диффузии ![]() и в общем случае является функцией скорости ветра:
и в общем случае является функцией скорости ветра:


Рисунок 5. Изменение эффективного коэффициента диффузии с изменением скорости ветра
Аналитические и численные исследования распространения газовых загрязнителей в атмосфере при наличии и отсутствии атмосферных осадков показали, что с большим течением времени концентрация рассеивается в атмосфере. Кроме того, ветер с большой скоростью может уносить загрязнители на большие расстояния. Используемый математический аппарат удобен для графических иллюстраций процесса распространения вредных веществ в атмосфере. Результаты исследований могут быть использованы при исследовании процесса превращения газообразных веществ в более сложные соединения в атмосфере, такие как кислотные дожди и аэрозоли. Исследования также удобны для проектировании промышленных объектов с целью учёта вредного влияния выбросов на окружающую среду.
Список литературы:
1.Берлянд М.Е. Современные проблемы атмосферной диффузии и загрязнения атмосферы. — Л.: Гидрометеоиздат, 1975. — 449 с.
2.Замай С.С., Якубайлик О.Э. Моделирование оценки и прогноза загрязнения атмосферы промышленными выбросами в информационно-аналитической системе природоохранных служб крупного города: Учебное пособие. — Красноярск: Красноярский Государственный Университет, 1998. — 109 с.
3.Калиткин Н.Н., Карпенко Н.В., Михайлов А.П., В.Ф. Тишкин. Моделирование процессов природы и общества. — М.: Физматлит, 2005. — 360 с.
4.Степаненко С.Н., Волошин В.Г., Типцов С.В.. Решение уравнения турбулентной диффузии для стационарного и точечного источника / Украинский экологический журнал. — О: Одесский государственный экологический университет, 2007. — 24 с.
дипломов





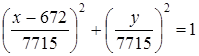
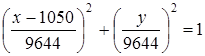
Комментарии (2)
Оставить комментарий