Статья опубликована в рамках: XVIII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 20 февраля 2013 г.)
Наука: Технические науки
Секция: Транспорт и связь, кораблестроение
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ГАЛОПИРОВАНИЕ ЦИЛИНДРОВ С ПЛАВНЫМИ ОБВОДАМИ
Люсин Виталий Дмитриевич
ведущий инженер СПбГУ, г. Санкт-Петербург
THE GALLOPING OF THE CYLINDERS WITH SMOOTH CURVES
Lyusin Vitaliy Dmitrievich
Leading engineer, St. Petersburg state University, Saint-Petersburg
АННОТАЦИЯ
Проведены измерения аэродинамических сил, действующих на цилиндры, имеющие криволинейные основания без острых кромок. Установлено наличие двух режимов обтекания в некотором диапазоне углов атаки. Разработана модель аэроупругого галопирования тел с подобными аэродинамическими характеристиками. Расчеты с использованием новой модели, дали зависимости амплитуды колебаний от скорости набегающего потока для цилиндров различного удлинения.
ABSTRACT
The aerodynamic forces acting on the cylinders with curved bases without sharp edges are measured. The existence of two flow regimes is established in a certain range of angles of attack. A model of aeroelastic galloping of the bodies with similar aerodynamic characteristics is developed. The calculations according the new model gave the dependences of oscillation amplitude on the incoming flow velosity for cylinders of different extension.
Ключевые слова: галопирование, плохообтекаемое тело, моделирование колебаний, эксперимент.
Key words: galloping, bluff body, oscillation simulation, experiment.
1. Введение. Неосесимметричные цилиндры являются неотъемлемой частью многих элементов транспортных средств. Примером могут служить вагоны подвесной канатной дороги. Тела, с точки зрения их аэродинамических характеристик, можно разделить на два класса: удобообтекаемые и плохообтекаемые. Основной особенностью плохообтекаемых тел является отрыв пограничного слоя при взаимодействии их с потоком газа или жидкости [1]. Это может приводить к нестабильности и колебаниям таких тел под воздействием ветра или течений. Большинство мостов зданий и прочих инженерных конструкций являются как раз плохообтекаемыми телами. Известны даже случаи разрушения мостов под воздействием ветра, например мост Такома Нерроуз [3].
Одной из причин, вызывающих колебания плохообтекаемых тел, является галопирование. Оно обусловлено специфическими зависимостями аэродинамических характеристик объектов от углов атаки. Впервые модель аэроупругого галопирования была предложена Паркинсоном и его соавторами в середине XX-го века [8, 9]. Позднее эта модель не раз использовалась различными учеными для проведения исследований в этой области [6, 7]. Большой вклад в изучение галопирования внес Новак [7]. Он проводил эксперименты с призмами различных прямоугольных сечений. В последнее время появилось множество работ, в которых исследуются цилиндры с треугольными [4], ромбовыми [5] и даже криволинейными сечениями [5]. Изучался также вопрос влияния числа Рейнольдса на характер и склонность к галопированию [6].
Эффекту галопирования подвержены не только тела большого удлинения, такие как мосты, колонны или трубопроводы, но и малого. Вопрос о влиянии удлинения квадратных призм на амплитуду возможных колебаний изучался автором ранее [2]. Данная работа посвящена исследованию галопирования цилиндров разного удлинения, боковые поверхности которых не имеют острых кромок. Сечение цилиндров приближенно напоминает сечение железнодорожных вагонов или вагонов подвесной канатной дороги.
Постановка задачи и математическая модель.
Рассматривается тело, упруго закрепленное в потоке газа. Предполагается, что тело может двигаться только в направлении перпендикулярном потоку. В этом же направлении на него действуют три силы: упругая, аэродинамическая и сила вязкого демпфирования, не связанная с аэродинамикой (трение в подвеске и тому подобное). Эти три силы входят в уравнение движения призмы в поперечном направлении. Аэродинамическую силу, действующую на колеблющееся тело, предлагается считать равной силе, действующей на стационарно закрепленное тело при соответствующих углах атаки (квазистатическое приближение). Таким образом, проведя эксперимент над стационарно закрепленным телом и измерив силы, действующие на него при различных углах атаки, можно приблизить эти данные некоторой функцией, подставить ее в уравнение движения и, решив его, найти зависимость между скоростью набегающего потока и амплитудой колебаний. Более подробно модель изложена в работе посвященной прямоугольным призмам [2].
2. Проведение экспериментов. Объектом исследования в данной работе были три цилиндра имеющие в сечении одну и ту же криволинейную, выпуклую фигуру. Отношения длины цилиндра к диаметру основания составляли 2, 4 и 8 соответственно для каждого из трех тел. Эксперимент проводился в аэродинамической трубе с открытой рабочей частью. Цилиндры были жестко закреплены. Углы атаки менялись от –30 до 30 градусов. Были проведены измерения аэродинамических сил действующих на тела при числе Рейнольдса Re=2*104. После этого были вычислены аэродинамические коэффициенты нормальной силы Cn для всех трех тел. Результаты приведены на рисунке 1. На рисунке 2 приведены аналогичные результаты для прямоугольной призмы с квадратным основанием (острыми кромками).
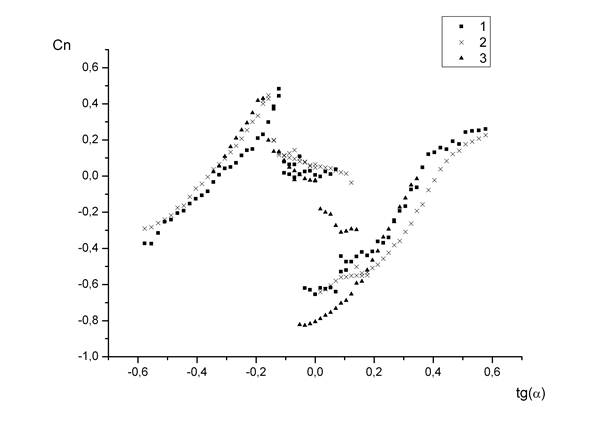
Рисунок 1. Cn для цилиндров с закругленными кромками различного удлинения (λ); 1 — λ=2, 2 — λ=4, 3 — λ=8

Рисунок 2. Cn для прямоугольной квадратной призмы удлинения 10
Принципиальным отличием тел с закругленной кромкой, обнаруженным во время эксперимента, стало наличие двух режимов обтекания при некоторых углах атаки. Режим обтекания, а соответственно и сила, действующая на тело, зависели от того, какое положение относительно потока исследуемый макет занимал до момента измерения. Это противоречит идее об использовании квазистатического приближения, согласно которой аэродинамические силы должны зависеть только от углов атаки. Однако, проведя серию экспериментов, удалось сделать эмпирическое предположение о наличии для каждого тела двух критических углов атаки, при переходе через которые меняется режим обтекания. Значения этих критических углов совпадают с границами области двойственности обтекания. Таким образом, когда тело, меняя свое положение в потоке и, соответственно, угол атаки, переходит через одну границу, устанавливается первый режим обтекания, при переходе через другую границу режим меняется на второй. Это предположение позволило использовать полученные данные для составления уравнения движения.
Использование метода Крылова-Боголюбова для решения уравнения движения и результаты.
В общем виде, уравнение движения колеблющегося тела, записанное в безразмерных координатах, выглядит следующим образом:
![]() . (1)
. (1)
Здесь у — смещение тела от положения равновесия. Функция F является представлением результирующей сил вязкого демпфирования и аэродинамической нагрузки. В классической модели аэроупругого галопирования предлагается приближать коэффициент аэродинамической силы полиномом тангенса угла атаки. В таком случае функция F будет иметь вид многочлена. Для решения задачи о колебании цилиндров с закругленной кромкой такая аппроксимация функции невозможна из-за наличия двух режимов обтекания в некотором диапазоне углов атаки. Предлагается искать решение в виде:
![]() .
.
Здесь амплитуда A и фаза p — медленно меняющиеся функции временного параметра t1. Умножая уравнение (1) на ![]() получим:
получим:
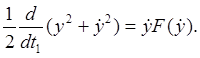
Что при подстановке у и ![]() дает:
дает:
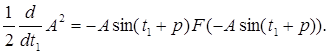
Воспользуемся предположением о малости периода по сравнению со временем изменения амплитуды колебаний. Усредним правую часть уравнения по периоду цикла. Получим:
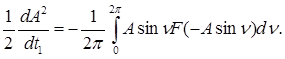 (2)
(2)
В случае, когда функция F является многочленом, можно подставить ее в уравнение, вычислить интеграл, а затем, приравняв к нулю правую часть, для поиска установившихся решений получить алгебраическое уравнение для нахождения амплитуды колебаний. Параметром этого уравнения будет безразмерная скорость потока, которая входила также в качестве параметра в функцию F. Результатом большинства работ является построение графика зависимости безразмерной амплитуды колебаний от безразмерной скорости.
Для тел имеющих диапазон углов атаки с двумя режимами обтекания предлагается использовать в качестве аппроксимации Cn кусочную функцию. На каждом отдельном участке она будет являться многочленом. Представление интеграла в уравнении (2) в виде аналитического выражения приводит к довольно громоздким формулам, поэтому было решено вычислять этот интеграл численно. Преобразованное таким образом уравнение (2) решалось также численно методом Рунге-Кутты. Задав значение безразмерной скорости потока и начальное значение амплитуды, можно определить, как будут развиваться колебания. Таким образом, были вычислены амплитуды установившихся колебаний. Для нахождения неустойчивых решений достаточно определить, при каком значении начальной амплитуды правая часть уравнения (2) меняет знак. А изменяя значение безразмерной скорости потока можно построить график зависимости амплитуды колебаний от скорости потока в любом необходимом диапазоне. Пример аппроксимации Cn для цилиндра с закругленными кромками представлен на рисунке 3. На рисунке 4 приведены результаты вычисления зависимости амплитуды (A) от скорости потока (ν) по предложенной схеме.
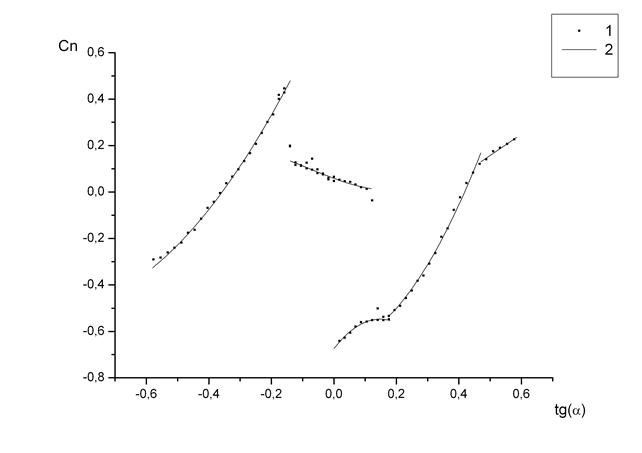
Рисунок 3. Пример аппроксимации коэффициента нормальной силы Cn кусочной функцией (λ=4). 1 — экспериментальные данные, 2 — аппроксимирующая функция
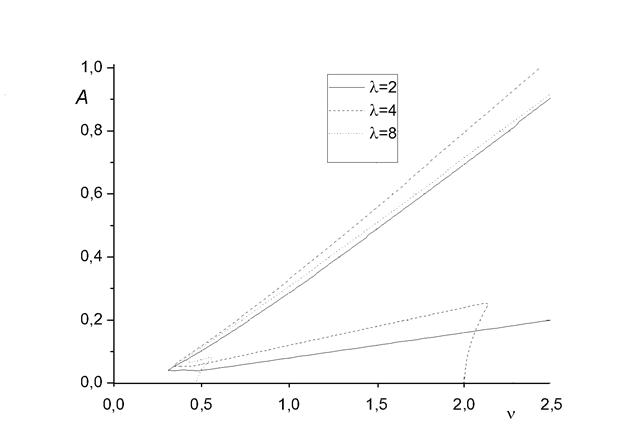
Рисунок 4. Зависимость амплитуды установившихся колебаний (A) от скорости набегающего потока (ν) для цилиндров с закругленными кромками различных удлинений (λ)
Стоит отметить, что, как и в случае с квадратными призмами, критическая скорость (скорость потока при которой положение равновесия становиться неустойчивым) уменьшается при увеличении удлинения тела. На графике критическая скорость это координата точки пересечение соответствующей линии с осью абсцисс. Значение максимальной амплитуды колебаний от удлинения практически не зависит.
3. Выводы. В настоящей работе экпериментально определены коэффициенты аэродинамических сил, действующих на стационарно закрепленные цилиндры с закругленными кромками. Обнаружено, что в некоторых диапазонах углов атаки существует два режима обтекания, причем выбор одного из режимов определяется предысторией потока. Разработана математическая модель галопирования, учитывающая переходы между различными режимами. Предложены аппроксимации для описания зависимости коэффициента нормальной силы от угла атаки. На основе предложенной модели вычислены амплитуды колебаний цилиндров разного удлинения в зависимости от скорости набегающего потока. Проведено сравнение движения исследуемых цилиндров с поведением в потоке квадратных призм.
Список литературы:
1. Девнин С.И. Аэрогидромеханика плохообтекаемых конструкций.— Л.: Судостроение, 1983. 332 с.
2. Люсин В.Д., Рябинин А.Н. Исследование влияния удлинения призмы на ее аэродинамические характеристики и амплитуду колебаний призмы при галопировании. // Вестник СПбГУ Сер. 1 — 2011. — Вып. 2. — C. 139—145.
3. Томпсон Дж.М.Т. Неустойчивость и катастрофы в науке и технике. — М.: Мир. 1985.
4. Alonso G., Meseguer J., Perez-Grande I. Galloping instabilities of two-dimensional triangular cross-section bodies // Experiments in Fluids. — 2005. — Vol. 38. — P. 789—795.
5. Alonso G., Meseguer J., Valero E. An analysis on the dependence on cross section geometry of galloping stability of two-dimensional bodies having either biconvex or rhomboidal cross sections // European J. Mech B / Fluids. — 2009. — Vol. 28. — P. 328—334
6. Barrero-Gil A., Sanz-Andres A., Roura M. Transverse galloping at low Relnolds numbers // J. Fluid and Structures. — 2009. — Vol. 25. — P. 1236—1242.
7. Novak M. Aeroelastic galloping of prismatic bodies // J. Engineering Mech. Division ASCE. — 1969. — Vol. 95. — P. 115—142.
8. Parkinson G.V., Brooks N.P. On the Aeroelastic Instability of Bluff Cylinders // J. Appl. Mech. — 1961. — Vol. 28. — P. 252—258.
9. Parkinson G.V., Smith J.D. The square prisms as an aeroelastic non-linear oscillators // Quarterly J. Mech. Applied Math. — 1964. — Vol. XVII Pt. 2 — P. 225—239.
дипломов


Оставить комментарий