Статья опубликована в рамках: X Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 28 мая 2012 г.)
Наука: Технические науки
Секция: Энергетика и энергетические техника и технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ ДЕЙСТВИЯ ЧАСТОТНОЙ ДЕЛИТЕЛЬНОЙ АВТОМАТИКИ СИСТЕМЫ ЭЛЕКТРОСНАБЖЕНИЯ МЕГАПОЛИСА
Костин Владимир Николаевич
канд. техн. наук, доцент СПбГГУ, г. Санкт-Петербург
Кравченко Илья Владимирович
аспирант СПбГГУ, г. Санкт-Петербург
IMPROVING THE EFFICIENCY OF THE SYSTEM OF AUTOMATIC FREQUENCY DIVIDING POWER MEGAPOLIS
Vladimir Kostin
Ph.D., Associate Professor of St. Petersburg State Mining University, St. Petersburg
Ilya Kravchenko
St. Petersburg State Mining University graduate student, St. Petersburg
АННОТАЦИЯ
Для повышения эффективности действия частотной делительной автоматики системы электроснабжения мегаполиса необходимы достоверные данные о нагрузках района потенциального выделения на текущий момент времени. Предложена аппроксимация сплайнами результатов контрольных замеров нагрузки, осуществляемых ежегодно в июне и декабре. Результаты промежуточных замеров нагрузки на одной из подстанций энергосистемы Санкт-Петербурга показали удовлетворительное совпадение с результатами аппроксимации.
ABSTRACT
To improve the efficiency of the frequency dividing power system automation metropolis requires reliable data on the load area of potential allocation for the current time. Proposed approximation by splines of the results of control measurements of the load carried out annually in June and December. The results of measurements of the intermediate load on one of the substations of the power supply system of St. Petersburg showed good agreement with the results approximated.
Ключевые слова: эффективность частотной делительной автоматики; автоматическая частотная разгрузка; контрольные замеры нагрузки подстанций; аппроксимация сплайнами результатов замеров.
Keywords: efficiency of the frequency dividing automation; auto-cal frequency discharge; control measurements of load substations; the approximation of the results of measurements.
Системные аварии в Москве (2005 г.) и Санкт-Петербурге (2010 г.) нанесли большой экономический, политический и общественно-социальный ущерб и обусловили необходимость разработки мероприятий по совершенствованию комплексов противоаварийной автоматики, в том числе частотной делительной автоматики (ЧДА) и автоматической частной разгрузки (АЧР) [2].
Для обеспечения эффективного действия ЧДА при аварийном выделении энергорайона мегаполиса необходима следующая информация: схема сети района, величина генерации электростанций района, величина нагрузки потенциально выделяемого района, объём нагрузки, подведенной под АЧР.
В настоящее время схема сети и генерация электростанций района потенциального выделения осуществляются достаточно точно с помощью существующей системы телеизмерений (ТИ). Оценка же величины нагрузки района и объема нагрузки, подведенной под АЧР, при существующем в энергосистемах мегаполисов недостаточном уровне развития системы ТИ осуществляется, как правило, по данным контрольных замеров, выполняемых два раза в год.
Следует отметить, что в условиях мегаполиса количество подстанций и комплектов АЧР, реализованных на этих подстанциях для районов, входящих в зону действия ЧДА, может достигать сотни и более. В этих условиях для повышения эффективности ЧДА необходимо проведение многочисленных расчётов по определению требуемого баланса генерации и потребления. Поэтому достоверная оценка величины нагрузки и ее объема, подведенного под АЧР в районе действия ЧДА, является весьма актуальной и трудоёмкой задачей, которая должна решаться в темпе реального времени. Автоматизация этого процесса обеспечит принятие обоснованных решений по выбору направления действия ЧДА и повышение надежности электроснабжения мегаполиса.
В настоящее время в Филиале ОАО «СО ЕЭС» Ленинградское РДУ осуществляется разработка программного комплекса (ПК) «Система контроля эффективности действия ЧДА» для мониторинга всех районов потенциального выделения в энергосистеме Санкт-Петербурга и Ленинградской области [3].
Рассмотрим основные принципы организации мониторинга режимных параметров, имеющимися средствами контроля текущей информации: оперативно-информационным комплексом (ОИК), результатами контрольных замеров нагрузки, осуществляемыми ежегодно в июне и декабре.
Величина мощности генераторов, остающихся в выделившемся районе после действия ЧДА, будет использоваться в ПК «Система контроля эффективности действия ЧДА», благодаря созданию интерфейса для одной из подпрограмм ОИК.
Определение текущей нагрузки района может осуществляться с помощью ТИ перетоков активной мощности по элементам связи района потенциального выделения с энергосистемой. Нагрузка этого района определится как:
Рнагр(t)=∑Рг(t)+∑Рс(t), (1)
где ∑Рг(t) – суммарная генерация электростанций района;
∑Рс(t) – суммарная мощность, поступающая в район из системы или поступающая из района в систему.
Для районов, не оснащённых средствами ТИ, будут использоваться данные о нагрузках, полученные по результатам контрольных замеров. С этой целью для каждой подстанции района формируются массивы значений нагрузок Рнагрi и объема нагрузки, подведенной под АЧР РАЧР i (табл. 1).
Таблица 1
Массивы значений нагрузок для подстанции
|
Оперативное название подстанции |
|||||||
|
Дата контрольного замера |
|||||||
|
Час |
1 |
2 |
3 |
… |
… |
23 |
24 |
|
Рнагр i, МВт |
Рнагр 1 |
Рнагр 2 |
Рнагр 3 |
… |
… |
Рнагр 23 |
Рнагр 24 |
|
РАЧР i, МВт |
РАЧР 1 |
РАЧР 2 |
РАЧР 3 |
… |
… |
РАЧР 23 |
РАЧР 24 |
На базе таких массивов определяется нагрузка района потенциального выделения Рнагр и нагрузка, подведенная под АЧР Рнагр. Эта информация, справедливая только для дней контрольных замеров, является единственной для определения величины нагрузки района Рнагр(t) и РАЧР(t) на произвольный (текущий или перспективный) момент времени t. На основании этих данных и текущей генерации района ∑Рг(t) делается вывод о сбалансированности района потенциального выделения и необходимости ввода-вывода некоторых комплектов ЧДА на текущий момент времени t.
Очевидно, что данные контрольных замеров нагрузки, осуществляемых два раза в год, могут существенно отличаться от режима нагрузки текущего момента времени t и снизить эффективность действия ЧДА. Поэтому при определении нагрузки в произвольный текущий (или перспективный) момент времени t возникает задача интерполяции результатов контрольных замеров.
В настоящей работе предлагается интерполяция сплайнами результатов контрольных замеров нагрузки. Это быстрый, эффективный и устойчивый способ интерполяции функций, являющийся одной из альтернатив полиномиальной интерполяции [1].
Для получения сплайн-интерполяции используется Maple-функция
spline (X, Y, var, d), (2)
где X и Y – одномерные векторы одинакового размера, несущие значения координат узловых точек исходной функции;
var – имя переменной, относительно которой вычисляется сплайн-функция;
d – параметр, задающий вид сплайна (порядок полинома).
Наиболее распространенной является сплайн-интерполяция на основе полиномов третьего порядка (d=3). Коэффициенты полинома подбираются таким образом, чтобы выполнялись требования непрерывности функции и, разумеется, прохождение через предписанные точки. Дополнительным требованием является непрерывность высших производных.
Благодаря плавности сплайн-кривых они хорошо описывают функции, представленные любым числом N узловых точек, поскольку порядок полиномов от этого числа не зависит. Системы линейных уравнений, которые требуется решать для построения сплайнов, хорошо обусловлены и даже при очень больших N вычислительная схема не теряет устойчивость.
Таким образом, сплайновая функция представляет собой кусочную функцию, определяемую на каждом отдельном интервале. При этом на каждом участке такая функция описывается отдельным полиномом
![]()
![]() (3)
(3)
Коэффициенты полинома аi, bi, ci, di на каждом интервале определяются из условий в узлах, в соответствии с которыми многочлен должен принимать заданные значения функции
![]()
![]() (4)
(4)
![]()
![]() (5)
(5)
Число этих уравнений вдвое меньше числа неизвестных коэффициентов, поэтому для определенности задачи вводятся дополнительные условия. Для их получения вычисляются первая и вторая производные многочлена (3)
![]() (6)
(6)
![]() при ti-1<t<ti, (7)
при ti-1<t<ti, (7)
и вводится требование непрерывности этих производных во всех точках, включая узлы. Приравнивая в узле ti правые и левые пределы производных, получим
![]() 1<i<N-1, (8)
1<i<N-1, (8)
![]() 1<i<N-1, (9)
1<i<N-1, (9)
Недостающие два условия можно получить из естественного предположения о нулевой кривизне функций на концах.
![]() (10)
(10)
![]() (11)
(11)
Уравнения (8—11) образуют систему линейных уравнений для определения 4N неизвестных коэффициентов, которая может быть решена, например, методом Гаусса. Однако эту систему сначала целесообразно привести к специальному виду. Уравнение (4) позволяет определить все коэффициенты ai. Из уравнений (9—11) следует, что
 при 1<i<N-1, (12)
при 1<i<N-1, (12)
![]() (13)
(13)
После подстановки (12) в (5) и исключения оттуда ai – yi-1, получим
 1<i<N-1, (14)
1<i<N-1, (14)
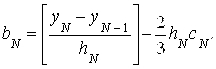 (15)
(15)
Исключая из (8) с помощью (14) величины bi и bi+1 и принимая di по (12), получим систему линейных уравнений для ci
ci=0, (16)
 при 2<i<N, (17)
при 2<i<N, (17)
cN+1=0. (18)
После нахождения значений ci остальные коэффициенты вычисляются по выражениям (4, 5, 12, 13, 14 и 15).
Использование указанного алгоритма к расчёту нагрузки района потенциального выделения на текущий (или перспективный) момент времени t иллюстрируется на рис. 1.

Рис. 1. Иллюстрация аппроксимации сплайнами результатов контрольных замеров
Точками 1, 2, … 6 отмечены максимальные нагрузки некоторой подстанции июньского и декабрьского дней 2009—2011 гг. Сплошной линией показана сплайн-интерполяция результатов замеров нагрузки за указанные годы. Пунктирная линия показывает перспективное изменение нагрузки в 2012 г. Эта кривая принимается по предшествующему 2011 году, однако начало кривой лежит в узле 6, расположенном выше узла 4, что позволяет учесть годовой прирост нагрузки. Квадратом отмечена вероятная максимальная мощность нагрузки текущего момента времени t.
Результаты внеочередных замеров нагрузки на одной из подстанций системы электроснабжения Санкт-Петербурга, выполненные в октябре 2011 года, показали, что отличие максимальной измеренной нагрузки подстанции от нагрузки, полученной интерполяцией сплайнами, не превысило 5 %. При этом отличие результатов замеров летнего и зимнего максимумов нагрузки на этой подстанции составило более 40 %.
Выводы:
1. Для эффективного действия ЧДА необходимы достоверные данные по нагрузкам района потенциального выделения на текущий и перспективный моменты времени. Результаты контрольных замеров нагрузки, осуществляемых ежегодно в июне и декабре, могут существенно отличаться от величин нагрузок текущего момента времени и снизить эффективность действия ЧДА.
2. Предложена аппроксимация сплайнами результатов ежегодных контрольных замеров нагрузки, позволяющая более точно прогнозировать величину текущей и перспективной нагрузки района потенциального выделения и повысить эффективность действия ЧДА.
Список литературы:
1.Калиткин Н.Н. Численные методы. М., Наука, 1978. – 513 с.
2.Отчет по расследованию аварии в ЕЭС России, происшедшей 25.05.2005 // РАО "ЕЭС России". – 2005.
3.Принципы построения автоматизированной системы контроля эффективности действия ЧДА / И.В. Кравченко и [др.] // Научно-технические ведомости СПбГПУ. Наука и образование. – 2011. – № 4 (135). – С. 94—99.
дипломов


Оставить комментарий