Статья опубликована в рамках: X Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 28 мая 2012 г.)
Наука: Технические науки
Секция: Энергетика и энергетические техника и технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
расчет теплопередачи в рабочей стенке щелевого кристаллизатора машины непрерывного литья заготовок
Кибардин Антон Николаевич
аспирант кафедры «Промышленная теплоэнергетика», ЧГУ, г. Череповец
Е-mail: anton_kibardin@mail.ru
Лукин Сергей Владимирович
канд.техн.наук, доцент, профессор ЧГУ, г. Череповец
Е-mail: s.v.luk@yandex.ru
The calculation of heat transfer in the slit mould wall of the continuous casting machine
Anton Kibardin
post-graduate student of “Industrial heat-power engineering” department, Cherepovets State University, Cherepovets
Sergey Lookin
candidate of technical sciences, professor of Cherepovets State University, Cherepovets
Аннотация
В статье представлена инженерная методика расчета теплопередачи в рабочей стенке щелевого кристаллизатора машины непрерывного литья заготовок, позволяющая достаточно точно учитывать эффект оребрения стенки со стороны охлаждающей воды.
ABSTRACT
In the paper is presented the engineering method of calculation of heat transfer in the slit mould wall of the continuous casting machine, allowing to take rather exactly account of the wall ribbing effect on the side of cooling water.
Ключевые слова: Теплопередача; кристаллизатор; машина непрерывного литья заготовок.
Key words: Heat transfer; mould; continuous casting machine.
Современные машины непрерывного литья заготовок часто оборудуют щелевыми кристаллизаторами, в которых охлаждающая вода циркулирует в пазах, расположенных между медной стенкой и чугунным корпусом. В настоящее время отсутствуют достаточно точные инженерные методики расчета теплопередачи в рабочей стенке щелевого кристаллизатора.
Схема рабочей стенки щелевого кристаллизатора и основные геометрические размеры показаны на рис. 1, где приведены следующие обозначения: 1 – медная плита; 2 – стальная пластина; 3 – прямоугольный паз, заполненный охлаждающей водой; 4 – рабочая поверхность стенки кристаллизатора; d – толщина стенки от рабочей поверхности до основания паза; 2s – расстояние между пазами; h – глубина паза (длина ребра); 2l – ширина паза (канала); q – плотность теплового потока, поступающего к рабочей стенке от затвердевающего слитка.
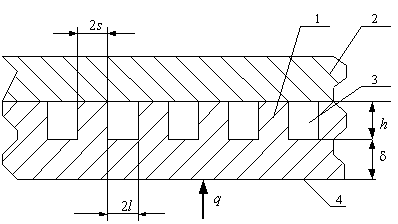
Рис. 1. Схема рабочей стенки щелевого кристаллизатора.
Расчетная схема элемента рабочей стенки щелевого кристаллизатора показана на рис. 2. На рис. 2 показано, что поверхностью 1 рабочая стенка контактирует с отливаемым слитком, а поверхностью 3 и 4 – с охлаждающей водой. Поверхность 5 соприкасается с чугунным корпусом. На поверхностях 2 и 6 выполняется условие геометрической и тепловой симметрии, поэтому здесь теплообмен отсутствует (адиабатические поверхности). Размеры ребра: h´s. Размеры основания стенки: d´(s+l).
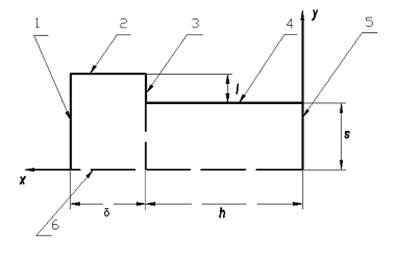
Рис. 2. Расчетная схема элемента рабочей стенки.
Для расчета эффективного коэффициента теплоотдачи от рабочей стенки щелевого кристаллизатора к охлаждающей воде, учитывающего эффект оребрения, можно использовать выражение, полученное в [1]:
![]() (1а)
(1а)
где Е – коэффициент эффективности оребрения, определяемый выражением:
![]() (1б)
(1б)
где α – обычный коэффициент теплоотдачи от поверхности к охлаждающей воде; λ – коэффициент теплопроводности материала стенки; d, s, l, h - геометрические размеры рабочей стенки, показанные на рис. 1.
Однако в щелевых кристаллизаторах ребра имеют достаточно большую толщину, поэтому выражение (1) дает существенную погрешность, т. к. получено в предположении одномерности температурного поля в ребрах, что для толстых ребер не выполняется. Получим решение, учитывающее двухмерность температурного поля в ребрах.
Введем избыточную температуру ![]() где t – температура стенки; tв – температура охлаждающей воды, выбранная за начало отсчета. Температурное поле стенки опишется уравнением Лапласа:
где t – температура стенки; tв – температура охлаждающей воды, выбранная за начало отсчета. Температурное поле стенки опишется уравнением Лапласа:
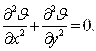 (2)
(2)
Рабочую стенку можно представить состоящей из двух элементов: основания стенки толщиной d и ребра. Ввиду малой толщины задачу расчета теплообмена в основании стенки считаем одномерной. Расчет температурного поля и термического сопротивления здесь не вызывает затруднений. Остановимся на расчете теплообмена в ребре длиной h и толщиной 2s. Граничные условия будут следующими:
![]()
![]()
![]()
![]()
где x, y – текущие координаты; ![]() – избыточная температура у основания ребра.
– избыточная температура у основания ребра.
С учетом граничных условий методом разделения переменных получено решение уравнения (2), описывающее температурное поле в ребре рабочей стенки щелевого кристаллизатора:
![]() (3)
(3)
![]()
Коэффициенты mk находятся из характеристического уравнения:
![]() , (4)
, (4)
где ![]() - критерий Био.
- критерий Био.
Известно, что корни mk уравнения (4) представляют бесконечную последовательность возрастающих чисел: m1<m2<…<mn<….. Поэтому ряд в (3) является быстро сходящимся для точек с координатой х<h.
Плотность теплового потока определяется законом Фурье:
![]() ,
,
где n – текущая координата. Из выражения (3) получим, что плотность теплового потока в ребре рабочей стенки кристаллизатора в направлении x в основании ребра равна:
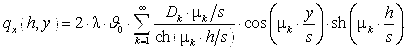 (5)
(5)
Для определения средней плотности теплового потока qх в основании ребра функцию (5) необходимо проинтегрировать на отрезке от 0 до s и разделить на длину этого отрезка s:

Тепловой поток, проходящий через половину основания ребра длиной 1 м (Вт/м) определится выражением:
 (6)
(6)
Тепловой поток, проходящий через половину основание паза, определяется выражением теплоотдачи к охлаждающей воде:
![]() . (7)
. (7)
Введем линейное термическое сопротивления ребра рабочей стенки кристаллизатора:
 8)
8)
Линейная плотность теплового потока рабочей стенки с учетом (6), (7) и (8) определяется выражением:
![]() (9)
(9)
где m – количество ребер в стенке.
Эффективный коэффициент теплоотдачи от рабочей стенки к охлаждающей воде определится выражением:
![]() (10)
(10)
где Р=2m×(s+l) – периметр рабочей стенки кристаллизатора.
С учетом (9) и (10) получим выражение для расчета aэф:
![]() (11)
(11)
где величина Rlp определяется выражением (8).
Обычный коэффициент теплоотдачи a определяется по известным эмпирическим зависимостям. Достаточно точной является формула Петухова [3], полученная при турбулентном течении капельных жидкостей и газов при 0,5<Pr<200 и 4000<Re<107:
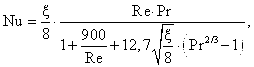 (12)
(12)
где ![]() - критерий Рейнольдса;
- критерий Рейнольдса; ![]() - критерий Нуссельта; Pr – число Прандтля для воды; x - коэффициент гидравлического сопротивления; w – средняя скорость движения воды в охлаждаемых каналах; dэ - эквивалентный диаметр канала; vв - коэффициент кинематической вязкости для воды; lв - коэффициент теплопроводности для воды. Величины vв, lв и Pr выбираются по средней температуре охлаждающей воды tв. Коэффициент x можно рассчитать по формуле [3]:
- критерий Нуссельта; Pr – число Прандтля для воды; x - коэффициент гидравлического сопротивления; w – средняя скорость движения воды в охлаждаемых каналах; dэ - эквивалентный диаметр канала; vв - коэффициент кинематической вязкости для воды; lв - коэффициент теплопроводности для воды. Величины vв, lв и Pr выбираются по средней температуре охлаждающей воды tв. Коэффициент x можно рассчитать по формуле [3]:
![]()
Эквивалентный диаметр прямоугольного канала определяется выражением:
![]()
где f=2l×2h – площадь сечения канала; р=2×(2l+2h) – периметр канала.
Рассмотрим пример. На вертикальной МНЛЗ сталеплавильного производства ЧерМК ОАО «Северсталь» применяется щелевой кристаллизатор со следующими геометрическими размерами рабочей стенки: h=0,025 м; l=0,0045 м; s=0,013 м; δ=0,02 м. Стенка выполнена из меди с коэффициентом теплопроводности λ =385 Вт/(м·К). Средняя температура охлаждающей воды - tв=30ºC. Скорость воды в каналах - w=6 м/с. При таких параметрах воды и размерах канала коэффициент теплоотдачи от стенки канала к воде, рассчитанный по формуле (12), равен a=20000 Вт/(м×К).
Определяем число Био: ![]() . Первые четыре корня характеристического уравнения (4) при этом Bi [2]: m1=0,74; m2=3,34; m3=6,39; m4=9,49. Расчет линейного термического сопротивления ребра по формуле (8) дает значение Rlр=0,00382 м К/Вт. Бесконечный ряд в (8) является быстросходящимся, и большая точность расчета достигается при использовании первых трех членов ряда. Расчет эффективного коэффициента теплоотдачи от стенки к воде по формуле (11) дает значение aэф=20110 Вт/(м2×К), что ненамного больше, чем обычный коэффициент теплоотдачи a, несмотря на то, что на 1 м2 плоской поверхности рабочей стенки приходится 1,69 м2 оребренной поверхности, взаимодействующей с водой. Это объясняется достаточно низким коэффициентом эффективности оребрения Е, который, рассчитанный по формуле (1б), в данном примере равняется 0,59. Более точно величину E можно рассчитать в рамках разработанной инженерной методики по выражению:
. Первые четыре корня характеристического уравнения (4) при этом Bi [2]: m1=0,74; m2=3,34; m3=6,39; m4=9,49. Расчет линейного термического сопротивления ребра по формуле (8) дает значение Rlр=0,00382 м К/Вт. Бесконечный ряд в (8) является быстросходящимся, и большая точность расчета достигается при использовании первых трех членов ряда. Расчет эффективного коэффициента теплоотдачи от стенки к воде по формуле (11) дает значение aэф=20110 Вт/(м2×К), что ненамного больше, чем обычный коэффициент теплоотдачи a, несмотря на то, что на 1 м2 плоской поверхности рабочей стенки приходится 1,69 м2 оребренной поверхности, взаимодействующей с водой. Это объясняется достаточно низким коэффициентом эффективности оребрения Е, который, рассчитанный по формуле (1б), в данном примере равняется 0,59. Более точно величину E можно рассчитать в рамках разработанной инженерной методики по выражению:
 (13)
(13)
Формула (13) дает для данного примера Е=0,52, т. е. существенно меньше, чем формула (1б). Для сравнения известной инженерной методики (формулы (1а) и (1б)) и разработанной инженерной методики (формулы (8) и (11)), был проведен численный расчет теплопередачи через рабочую стенку щелевого кристаллизатора при указанных условиях. Численный расчет позволяет учесть двухмерность температурного поля не только в ребре, но также в основании рабочей стенки, т. е. является более точным. Было получено, что численный расчет дает αэф = 19800 Вт/(м×К), известная инженерная методика - αэф=21840 Вт/(м К), разработанная инженерная методика - αэф=20110 Вт/(м К). Таким образом, αэф, полученный по известной инженерной методике, на 10,2 % превышает αэф, полученный численным методом. Значение αэф, полученное по разработанной инженерной методике, лишь на 1,5 % превышает αэф, полученное численно.
Таким образом, разработанная инженерная методика позволяет с хорошей точностью рассчитывать αэф на основе выражения (11). Инженерный расчет теплопередачи в рабочей стенке щелевого кристаллизатора проводится так же, как для плоской стенки толщиной d. Если известна плотность теплового потока q, проходящего через рабочую стенку кристаллизатора, то температура поверхности основания канала, заполненного водой, определяется выражением:
![]() (14а)
(14а)
Температуру рабочей поверхности стенки, контактирующей со слябом, можно оценить по выражению:
![]() (14б)
(14б)
Выражения (14) позволяют достаточно точно рассчитывать tосн.кан и tраб.пов, если плотность теплового потока q незначительно изменяется по высоте рабочей стенки кристаллизатора. В действительности, величина q быстро изменяется в верхней части кристаллизатора, что приводит к перетеканию теплоты вдоль рабочей стенки, и действительные температуры tосн.кан и tраб.пов получаются несколько другими, чем дают формулы (14). В верхней части кристаллизатора действительные температуры tосн.кан и tраб.пов будут меньше, чем рассчитанные по формулам (14), а в нижней части кристаллизатора – несколько больше. Так как надежность работы кристаллизатора во многом зависит от температур tосн.кан и tраб.пов на уровне мениска жидкого метала, где плотность теплового потока q является максимальной, то определение величин tосн.кан и tраб.пов по формулам (14) дает некоторый запас при расчетах надежной работы кристаллизатора.
Выводы: Представлена инженерная методика расчета теплопередачи в рабочей стенке щелевого кристаллизатора машины непрерывного литья заготовок, позволяющая достаточно точно учитывать эффект оребрения рабочей стенки со стороны охлаждающей воды.
Список литературы:
1.Калягин Ю.А., Шестаков Н.И., Манько О.В, Лукин С.В. Исследование теплообмена в кристаллизаторе МНЛЗ с круглыми щелевыми каналами // Заготовительные производства в машиностроении. – 2004. – № 12. – С. 29—31.
2.Лыков, А.В. Тепломассообмен: Справочник. – М.: Энергия, 1978. – 480 с.
3.Петухов Б.С., Поляков А.Ф. Теплообмен при смешанной турбулентной конвекции. – М.: Наука, 1986 . – 191 с.
дипломов


Комментарии (1)
Оставить комментарий