Статья опубликована в рамках: VI Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 16 января 2012 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С НЕЧЕТКИМИ ПАРАМЕТРАМИ
Стародубцев Игорь Юрьевич
преподаватель ВГУ, г. Воронеж
E-mail: starodubtsevigor@gmail.com
1. Введение
Во многих приложениях задачи нечеткого математического программирования (ЗНМП) рассматриваются как удобное и адекватное описание выбора в условиях неполной определенности. Математический аппарат решения подобных задач достаточно разнообразен и соответствует вариантам трактовки понятия оптимальности в различных условиях нечеткости. Если источником нечеткости являются параметры целевой функции или параметры ограничений, то исходная задачи НМП может рассматриваться как задача многокритериальной оптимизации с применением соответствующего математического аппарата, в том числе методов нечеткой логики [4, 2]. Часто решение задач с нечеткими параметрами сводится к задачам интервального программирования с соответствующими методами решения [1].
Будем рассматривать линейные модели принятия оптимальных решений в ситуации, когда целевая функция и ограничения содержат нечеткие параметры.
2. Решение ЗНЛП при нечетких параметрах целевой функции и ограничений
Рассмотрим следующую постановку задачи НЛП: требуется достичь максимального значения целевой функции
 , (1)
, (1)
при наличии ограничений
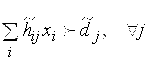 . (2)
. (2)
Коэффициенты целевой функции представляют собой нечеткие числа - ![]() , здесь и далее индексы L и R означают левую и правую границы носителя нечеткого числа. Нечеткие коэффициенты задаются экспертным путем. Параметры ограничений задаются как обычные числа,
, здесь и далее индексы L и R означают левую и правую границы носителя нечеткого числа. Нечеткие коэффициенты задаются экспертным путем. Параметры ограничений задаются как обычные числа, ![]() .
.
Требование максимизации исходной нечеткой целевой функции будем интерпретировать как максимизацию взвешенной суммы значений этой функции по ![]() -уровням
-уровням
![]() , (3)
, (3)
где 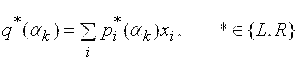 .
.
В ограничении (2) знак ![]() читается как «не хуже», то есть надо выбрать такой вектор х, который одновременно с условием (1) обеспечит левую часть выражения (2) «не хуже», чем правая часть. Такая интерпретация нечетких ограничений заключается в том, что точно описанное множество ограничений (допустимых альтернатив) оказывается лишь приближением реальности в том смысле, что в реальной задаче альтернативы вне множества точных ограничений могут быть не недопустимыми, а лишь в той или иной степени менее желательными для ЛПР, чем альтернативы внутри этого множества. Отношение «
читается как «не хуже», то есть надо выбрать такой вектор х, который одновременно с условием (1) обеспечит левую часть выражения (2) «не хуже», чем правая часть. Такая интерпретация нечетких ограничений заключается в том, что точно описанное множество ограничений (допустимых альтернатив) оказывается лишь приближением реальности в том смысле, что в реальной задаче альтернативы вне множества точных ограничений могут быть не недопустимыми, а лишь в той или иной степени менее желательными для ЛПР, чем альтернативы внутри этого множества. Отношение «![]() не хуже
не хуже ![]() » можно определить как «
» можно определить как «![]() содержится в
содержится в ![]() », то есть
», то есть ![]() . Другими словами выражение «
. Другими словами выражение «![]() содержится в
содержится в ![]() » можно рассматривать как
» можно рассматривать как ![]() . Как правило, левую часть (2) задает эксперт в рассматриваемой предметной области, а правую часть формулирует ЛПР. В такой интерпретации корректная запись неравенства (2) будет иметь вид
. Как правило, левую часть (2) задает эксперт в рассматриваемой предметной области, а правую часть формулирует ЛПР. В такой интерпретации корректная запись неравенства (2) будет иметь вид
![]() . (4)
. (4)
Предлагается следующая методика решения задачи (1-2). Критерий (1) записывается в виде четкой функции цели вида (3). Затем, в соответствии с методом, описанным в работе [3], вводятся дискретные ![]() -уровни, критерий и ограничения (4) рассматриваются применительно к каждому уровню
-уровни, критерий и ограничения (4) рассматриваются применительно к каждому уровню ![]() (
(![]() - число
- число ![]() -уровней). На уровне
-уровней). На уровне ![]() максимизируется соответствующее слагаемое критерия (3):
максимизируется соответствующее слагаемое критерия (3):
![]() (5)
(5)
Ограничения (4) записываются в виде системы интервальных ограничений на каждом ![]() -уровне:
-уровне:
![]() . (6)
. (6)
Приведение системы (6) к системе обычных линейных неравенств осуществляется записью отдельных неравенств с соответствующим отношением для левой и правой границ интервалов:
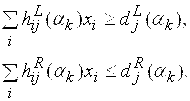 (7)
(7)
Таким образом, на каждом ![]() -уровне формируется обычная ЗЛП, решению которой приписывается соответствующее значение степени принадлежности, т. е.
-уровне формируется обычная ЗЛП, решению которой приписывается соответствующее значение степени принадлежности, т. е. ![]() -уровня. Окончательно формируется дискретное нечеткое множество решений исходной задачи. Решение в виде нечеткого множества само по себе достаточно информативно. Однако традиционный практический подход может потребовать четкого решения в виде обычного вектора х. В этом случае четкое решение можно получить, применяя один из известных методов дефаззификации, например, решение с максимальной функцией принадлежности или решение, взвешенное по методу «центра тяжести».
-уровня. Окончательно формируется дискретное нечеткое множество решений исходной задачи. Решение в виде нечеткого множества само по себе достаточно информативно. Однако традиционный практический подход может потребовать четкого решения в виде обычного вектора х. В этом случае четкое решение можно получить, применяя один из известных методов дефаззификации, например, решение с максимальной функцией принадлежности или решение, взвешенное по методу «центра тяжести».
Рассмотрим применение приведенной методики на следующем примере.
Будем рассматривать задачу начального распределения инвестиционных средств между двумя предприятиями с целью получения прибыли в течение двух последующих лет. Экспертные оценки прибыли ![]() с единицы инвестиционных средств в i-е предприятие имеют вид треугольных нечетких чисел:
с единицы инвестиционных средств в i-е предприятие имеют вид треугольных нечетких чисел: ![]() = (1; 3; 5),
= (1; 3; 5), ![]() = (1; 4; 6),
= (1; 4; 6), ![]() = (2; 3; 4),
= (2; 3; 4), ![]() = (0; 3; 6). Цель инвесторов – необходимо минимизировать суммарные инвестиции в оба предприятия, обозначив при этом нечеткие ограничения
= (0; 3; 6). Цель инвесторов – необходимо минимизировать суммарные инвестиции в оба предприятия, обозначив при этом нечеткие ограничения ![]() на ежегодную прибыль. Критерий оптимальности при этом принимает четкий вид:
на ежегодную прибыль. Критерий оптимальности при этом принимает четкий вид:
![]() , (8)
, (8)
что не мешает применять рассматриваемую методику, так как на каждом ![]() -уровне его выражение просто останется без изменений. Ограничения примут вид
-уровне его выражение просто останется без изменений. Ограничения примут вид
 (9)
(9)
![]()
Пусть ЛПР обозначил свои ограничения на прибыль первого и второго года в виде треугольных нечетких чисел ![]() =(2; 30; 60) и
=(2; 30; 60) и ![]() =(2; 30; 60). Зададим следующие
=(2; 30; 60). Зададим следующие ![]() - уровни: 0,2; 0,4; 0,6; 0,8; 1,0. Оптимальные решения
- уровни: 0,2; 0,4; 0,6; 0,8; 1,0. Оптимальные решения ![]() по
по ![]() - уровням показаны в таблице 1. Следует обратить внимание, что все ограничения согласно принятой интерпретации строго выполняются.
- уровням показаны в таблице 1. Следует обратить внимание, что все ограничения согласно принятой интерпретации строго выполняются.
Четкие ожидаемые оптимальные решения можно получить, используя методы дефаззификации:
 (10)
(10)
Таблица 1. Характеристики оптимальных решений по ![]() - уровням
- уровням
|
|
|
|
опт |
опт |
|
|
0,2 |
7,6=7,6 7,6=7,6 |
23,0<54,0 28,5<54,0 |
4,5 |
0,6 |
5,1 |
|
0,4 |
13,2=13,2 13,2=13,2 |
27,4<48,0 34,5<48,0 |
5,1 |
1,7 |
6,8 |
|
0,6 |
18,8=18,8 18,8=18,8 |
28,8<42,0 36,0<42,0 |
4,5 |
3,4 |
7,9 |
|
0,8 |
24,4=24,4 24,4=24,4 |
29,2<36,0 34,5<36,0 |
3,0 |
6,0 |
9,0 |
|
1,0 |
30=30 30=30 |
30=30 30=30 |
0 |
10,0 |
10,0 |
На основании данных таблицы 1 по формуле (10) получаем: ![]() =2,7;
=2,7; ![]() =5,9. При полученных значениях инвестиций в первое и второе предприятие совокупный доход за два года будет представлен нечетким числом
=5,9. При полученных значениях инвестиций в первое и второе предприятие совокупный доход за два года будет представлен нечетким числом
![]() =
= ![]() =(2; 7; 11)2,7+(2; 6; 10)5,9.
=(2; 7; 11)2,7+(2; 6; 10)5,9.
На основании правил перемножения нечетких чисел сначала получаем четкие интервалы на каждом ![]() - уровне нечетких чисел (четкие значения
- уровне нечетких чисел (четкие значения ![]() рассматриваются как частный случай нечеткого числа с
рассматриваются как частный случай нечеткого числа с ![]() - интервалом в виде соответствующей точки). Перемножая соответствующие концы интервалов, получим прибыль в виде нечеткого числа, заданного второй и третьей колонкой таблицы 2. В таблице 2 приведены также значения прибыли, получаемые при оптимальных решениях по
- интервалом в виде соответствующей точки). Перемножая соответствующие концы интервалов, получим прибыль в виде нечеткого числа, заданного второй и третьей колонкой таблицы 2. В таблице 2 приведены также значения прибыли, получаемые при оптимальных решениях по ![]() - уровням из таблицы 1, и значения левых и правых концов
- уровням из таблицы 1, и значения левых и правых концов ![]() - интервалов нечетких ограничений на прибыль.
- интервалов нечетких ограничений на прибыль.
Таблица 2. Прибыль в виде нечеткого числа
|
|
Прибыль при четком Решении |
Прибыль при решениях из таб. 1 |
Ограничения на прибыль |
|||
|
|
|
|
|
|
|
|
|
0,2 |
24,5 |
81,3 |
15,2 |
51,5 |
15,2 |
108,0 |
|
0,4 |
31,8 |
74,4 |
26,4 |
61,9 |
26,4 |
96,0 |
|
0,6 |
39,2 |
67,6 |
37,6 |
64,8 |
37,6 |
84,0 |
|
0,8 |
46,6 |
60,8 |
48,8 |
63,7 |
48,8 |
72,0 |
|
1,0 |
54,0 |
54,0 |
60,0 |
60 |
60,0 |
60,0 |
Полученная прибыль при четком решении не в полной мере согласуется с ограничениями (9), в отличие от решения в таблице 1. Как видно из таблицы 2, нарушение ограничений имеет место при ![]() равном 0,8 и 1,0: 46,6<48,8 и 54,0<60,0. Это объясняется заменой полученного в таблице 1 оптимального нечеткого решения его дефаззифицированным четким аналогом.
равном 0,8 и 1,0: 46,6<48,8 и 54,0<60,0. Это объясняется заменой полученного в таблице 1 оптимального нечеткого решения его дефаззифицированным четким аналогом.
Предложенная методика решения ЗНЛП позволяет получить оптимальное решение как в фаззифицированном, так и дефаззифицированном виде, хотя в последнем случае может возникать нарушение заданных нечетких ограничений. Если эти нарушения допустимы с точки зрения ЛПР и предложенная интерпретация оптимума критерия адекватна целям инвестора, то методика может применяться при решении задач нечеткого линейного программирования.
Список литературы:
1. Мелькумова Е. М. О решении некоторых задач нечеткого математического программирования / Вестник Воронежского государственного университета. Серия: «Системный анализ и информационные технологии», №2, 2009. - С. 19-24.
2. Семенов Б. А., Леденева Т. М. Многокритериальная оптимизация на основе нечеткой логики / Системы управления и информационные технологии. – М.; Воронеж: Науч. кн., 2009. - №1(35). – С. 43-47.
3. Яхъяева Г. Э. Нечеткие множества и нейронные сети. - ИНТУИТ.ru БИНОМ. Лаборатория знаний, 2008. – 320 с.
4. Klir G. Fuzzy sets and fuzzy logic: theory and applications / G. Klir, B. Yuan. – N.Y: Prentice Hall: Upper Saddle River, 1995.-574 p.
дипломов



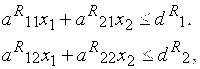
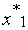
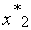

Комментарии (1)
Оставить комментарий