Статья опубликована в рамках: LV Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 24 февраля 2016 г.)
Наука: Технические науки
Секция: Приборостроение, метрология, радиотехника
Скачать книгу(-и): Сборник статей конференции
дипломов
ВЫБОР СТАТИСТИЧЕСКИ УСТОЙЧИВОЙ ПРОЦЕДУРЫ ИСКЛЮЧЕНИЯ ВЫБРОСОВ
SELECTION OF STATISTICALLY STABLE PROCEDURES FOR REMOVING OUTLIERS
Alexander Popov
candidate of Sciences, Department of mathematics
Baltic state technical university “VOENMEX” named after D.F. Ustinov,
Russia, St. Petersburg
АННОТАЦИЯ
В статье методами математического моделирования исследуется эффективность двух тестов по исключению выбросов в массиве градуировочных данных.
ABSTRACT
In article by the methods of mathematical modeling investigates the efficiency of two tests for the exclusion outliers in the array calibration data.
Ключевые слова: метод Граббса; метод Роснера; выбросы.
Keywords: Grubbs' test; generalized ESD test; outliers.
Многие статистические методы чувствительны к наличию выбросов. Например, простой расчет среднего и стандартного отклонения могут быть искажены единственным грубым наблюдением в данных.
Под выбросом, чаще всего, понимают наблюдение, которое значимо отличается по своей величине от остальных наблюдений выборки.
Проверка на выбросы должна быть обычной процедурой в каждом анализе данных. Потенциальные выбросы должны быть проинспектированы на предмет их возможной ошибочности. Если данное является ошибкой, оно должно быть по возможности исправлено или удалено. Если нет причин предполагать, что выделяющееся значения – ошибка, его удаление следует проводить после тщательного рассмотрения. В этом случае может быть оправдано использование робастных статистических процедур, которые часто снижают вес, с которым выбросы учитываются в ходе обработки данных.
Наряду с аналитическими алгоритмами для обнаружения очевидных выбросов могут быть использованы графические методы, например, гистограмма или «ящик с усами». Графическое представление данных помогает определиться с выбором алгоритма, то есть тестировать один или несколько выбросов, а также обнаружить возможные маскирующий или засасывающий эффекты.
В литературе предложено множество параметрических тестов для обнаружения выбросов. Их можно сгруппировать по следующим характеристикам: тип распределения, моделирующего данные; алгоритм тестирующий единственный выброс или группу выбросов; если тест спроектирован для определения серии выбросов, следует ли указывать точное число выбросов или достаточно указать для него верхнюю границу.
В настоящей работе исследуются наиболее распространенные тесты, основанные на критерии расстояния от среднего: последовательный тест Граббса (Grubbs’ Test) [1, с. 1–21], который рекомендуется для определения одиночного выброса, и блочный тест Роснера (General Extreme Studentized Deviate (ESD) Test) [2, c. 165–172], который требует только верхнее значения числа возможных выбросов в выборке и рекомендуется, когда точное число выбросов в выборке не известно.
Цель работы – исследовать эффективность указанных тестов в условиях специфики массива данных градуировочных испытаний, а именно:
- сравнительно небольшой объем выборки наблюдений;
- возможность наличия в выборке нескольких выбросов, причем число их заранее неизвестно;
- разнообразие и неконтролируемость законов распределений вероятностей основной совокупности наблюдений.
Тест Граббса используется для определения единственного выброса и применяется к данным, которые распределены по нормальному закону и имеют одинаковый разброс. Тест Граббса определяет следующие типы гипотез: нулевая гипотеза ![]() – в выборке нет выбросов; альтернативная гипотеза
– в выборке нет выбросов; альтернативная гипотеза ![]() – выборка содержит в точности один выброс. В качестве статистики критерия в двухсторонней версии теста используется наибольшее абсолютное отклонение выборочного среднего в единицах стандартного отклонения
– выборка содержит в точности один выброс. В качестве статистики критерия в двухсторонней версии теста используется наибольшее абсолютное отклонение выборочного среднего в единицах стандартного отклонения
![]() , 1)
, 1)
где: ![]() и
и ![]() – означают, соответственно, выборочное среднее и стандартное отклонение. При уровне значимости
– означают, соответственно, выборочное среднее и стандартное отклонение. При уровне значимости ![]() , нулевая гипотеза отклоняется, если
, нулевая гипотеза отклоняется, если
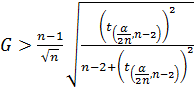 2)
2)
где: ![]() – критическая точка распределения Стьюдента с
– критическая точка распределения Стьюдента с ![]() степенями свободы.
степенями свободы.
Тест Роснера используется для определения одного или нескольких выбросов и применяется к данным, которые распределены приблизительно нормально и имеют одинаковый разброс. В тесте Роснера требуется определить лишь верхнюю границу возможного числа выбросов ![]() вместо указания их точного числа. В настоящей работе принято
вместо указания их точного числа. В настоящей работе принято ![]() . По существу, тест Роснера реализует
. По существу, тест Роснера реализует ![]() отдельных тестов: тест на один выброс, тест на два выброса и так далее вплоть до
отдельных тестов: тест на один выброс, тест на два выброса и так далее вплоть до ![]() выбросов. Тест Роснера определяет следующие типы гипотез: нулевая гипотеза
выбросов. Тест Роснера определяет следующие типы гипотез: нулевая гипотеза ![]() – в выборке нет выбросов; альтернативная гипотеза
– в выборке нет выбросов; альтернативная гипотеза ![]() – выборка содержит до
– выборка содержит до ![]() выбросов включительно. В качестве статистики критерия в двухсторонней версии теста используется
выбросов включительно. В качестве статистики критерия в двухсторонней версии теста используется
![]() , 3)
, 3)
где: ![]() и
и ![]() означают соответственно выборочное среднее и стандартное отклонение. Исключив наблюдение, которое максимизирует
означают соответственно выборочное среднее и стандартное отклонение. Исключив наблюдение, которое максимизирует ![]() , заново рассчитывается приведенная выше статистика по
, заново рассчитывается приведенная выше статистика по ![]() наблюдениям. Эта процедура повторяется пока все
наблюдениям. Эта процедура повторяется пока все ![]() наблюдений не будут удалены. Для каждого, полученного таким образом, значения
наблюдений не будут удалены. Для каждого, полученного таким образом, значения ![]() рассчитываются критические значения
рассчитываются критические значения ![]() :
:
 ,
, ![]() 4)
4)
где: ![]() – означает квантиль уровня
– означает квантиль уровня ![]() распределения Стьюдента с
распределения Стьюдента с ![]() степенями свободы и
степенями свободы и ![]() . Число выбросов определяется путем нахождения наибольшего
. Число выбросов определяется путем нахождения наибольшего ![]() , такого что
, такого что ![]() .
.
На этапе моделирования выброс в выборки объемом ![]() вводился случайно, при этом создавались маскирующий и засасывающий эффекты. Маскирующий эффект проявлялся в случае нескольких выбросов в выборке. Например, при тестировании единичного выброса методом Граббса, в то время, как на самом деле их несколько, эти дополнительные выбросы влияли на значение тестовой статистики, в результате чего ни один выброс не был обнаружен. Засасывающий эффект проявлялся в случае указания числа выбросов больше фактического. Например, при тестировании двух и более выбросов методом Роснера, в то время как на самом деле выброс был единственный – все множество подозрительных наблюдений объявлялось выбросами.
вводился случайно, при этом создавались маскирующий и засасывающий эффекты. Маскирующий эффект проявлялся в случае нескольких выбросов в выборке. Например, при тестировании единичного выброса методом Граббса, в то время, как на самом деле их несколько, эти дополнительные выбросы влияли на значение тестовой статистики, в результате чего ни один выброс не был обнаружен. Засасывающий эффект проявлялся в случае указания числа выбросов больше фактического. Например, при тестировании двух и более выбросов методом Роснера, в то время как на самом деле выброс был единственный – все множество подозрительных наблюдений объявлялось выбросами.
Основная совокупность данных генерировалась из широкого класса распределений, который включает: нормальное распределение ![]() , равномерное распределение
, равномерное распределение ![]() , экспоненциальное распределение
, экспоненциальное распределение ![]() . Уровень значимости выбирался равным
. Уровень значимости выбирался равным ![]() . Умеренным выбросом считалось наблюдение из интервала
. Умеренным выбросом считалось наблюдение из интервала ![]() ; большим выбросом – из интервала
; большим выбросом – из интервала ![]() . Эффективность отдельных процедур при каждом сочетании влияющих факторов оценивалась по схеме «успех–отказ» по каждому типу выбросов и их комбинаций по сериям из
. Эффективность отдельных процедур при каждом сочетании влияющих факторов оценивалась по схеме «успех–отказ» по каждому типу выбросов и их комбинаций по сериям из ![]() расчетов.
расчетов.
Вычислительный эксперимент проводился на языке и в программной среде статистического моделирования R [3]. В таблице 1 приведены усредненные значения частот исключения аномальных наблюдений.
Таблица 1.
Усредненные значения частот исключения выбросов
|
Метод |
Число выбросов |
Нормальное |
Равномерное |
Экспоненциальное |
|||
|
Объем выборки |
|||||||
|
|
|
|
|
|
|
||
|
Граббса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Роснера |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Результаты моделирования позволяют сделать следующие выводы:
- маскирующий эффект является основной причиной низкой эффективности последовательного применения теста Граббса, так как выбросы маскируют друг друга, в результате чего делается ложный вывод об их отсутствии;
- блочная процедура Роснера имеет эффективность не ниже
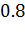 во всем диапазоне
во всем диапазоне  выбросов при объемах выборок не ниже
выбросов при объемах выборок не ниже 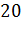 во всем классе рассматриваемых распределений;
во всем классе рассматриваемых распределений; - последовательная процедура Граббса сравнима с блочной процедурой Роснера при одном выбросе и заметно уступает ей при большем числе выбросов;
- комбинация из умеренных и больших выбросов обеими процедурами исключается реже, чем соответствующие выбросы по отдельности из-за эффекта «маскировки»;
- снижение объема выборки до 10 ухудшает эффективность процедуры Граббса на
 ,
,  и
и 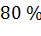 ; процедуры Роснера на
; процедуры Роснера на  ,
, 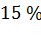 и
и 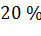 для одного, двух и трех выбросов соответственно.
для одного, двух и трех выбросов соответственно.
Таким образом, в реальных условиях анализа данных градуировочных наблюдений целесообразно ориентироваться на блочную процедуру Роснера, которая с вероятностью не ниже, чем ![]() исключает умеренные выбросы и практически достоверно – выбросы высокого уровня.
исключает умеренные выбросы и практически достоверно – выбросы высокого уровня.
Список литературы:
- Frank E. Grubbs. Procedures for Detecting Outlying Observations in Samples // Technometrics, 1969. – Vol. 11. – № 1.
- Rosner B. Percentage Points for a Generalized ESD Many Outlier Procedure. // Technometrics, 1983. – Vol. 25. – № 2.
- Core Team R.: A Language and Environment for Statistical Computing. // R Foundation for Statistical Computing, 2015.
дипломов


Оставить комментарий