Статья опубликована в рамках: LV Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 24 февраля 2016 г.)
Наука: Технические науки
Секция: Машиностроение и машиноведение
Скачать книгу(-и): Сборник статей конференции
дипломов
ОПТИМИЗАЦИОННО-МЕТРИЧЕСКИЙ СИНТЕЗ ШАРНИРНОГО ЧЕТЫРЕХЗВЕННИКА
METRIC OPTIMIZATION DESIGN OF ARTICULATED FOUR-BAR LINKAGE
Nurlan Beisenov
master of Science, senior lecturer of department of transportation and professional education of E.A. Buketov Karagandy State University,
Kazakhstan, Karagandy
АННОТАЦИЯ
Целью работы является получение приближенной шатунной кривой в виде наклонного эллипса шарнирного четырехзвенника. Предложенный алгоритм расчета проектных параметров механизма базируется на использовании методов оптимизации с применением компьютерной техники. Обоснована корректность и пригодность разработанной программы расчета оптимальных выходных параметров механизма по заданной шатунной кривой не только в виде наклонного эллипса, но и в виде окружности.
ABSTRACT
The objective of the work is the attainment of an approximate coupler curve in the form of an inclined ellipse of an articulated four-bar linkage. The suggested calculation algorithm of output mechanism parameters is based on the utilization of design methods using computer technology. The correctness and suitability of the created calculation program of optimal output mechanism parameters by the assigned coupler curve is substantiated not only in the form of an inclined ellipse, but also in the form of a circle.
Ключевые слова: шарнирный четырехзвенник; шатунная кривая; выходные параметры синтеза.
Keywords: articulated four-bar linkage; coupler curve; output design parameters.
Задача о построении механизма, который сможет удовлетворить всем наперед заданным условиям, издавна и по сей день интересует механиков. В сущности, она является одной из главнейших, если не самой главной, в кинематике механизмов. Проектирование любого механизма начинается с проектирования его схемы и определения постоянных параметров выбранной схемы механизма по заданным его свойствам. Оптимизация искомых параметров механизма с использованием современной компьютерной техники дает реальную возможность перебора вариантов случайных величин и решить любую задачу синтеза плоских механизмов.
Постановка задачи. В предлагаемой работе ставится задача получения приближенной шатунной кривой (траектории точки М) в виде наклонного эллипса шарнирного четырехзвенника, показанного на рисунке 1, удовлетворяющего условию существования кривошипа ![]() , при наложенных ограничениях на длины звеньев. В качестве проектных параметров оптимизации предлагается выбрать размеры звеньев механизма (а, b, с, f) при определенном значении расстояния между опорами d, а выбор оптимального решения проводить с помощью целевой функции, определяемой проектными параметрами.
, при наложенных ограничениях на длины звеньев. В качестве проектных параметров оптимизации предлагается выбрать размеры звеньев механизма (а, b, с, f) при определенном значении расстояния между опорами d, а выбор оптимального решения проводить с помощью целевой функции, определяемой проектными параметрами.

Рисунок 1. Синтезируемый шарнирный четырехзвенник. 1 – кривошип, 2 – шатун, 3 - коромысло
Ограничения. Первое ограничение – ограничение на длины звеньев a, b, c и d. Для того, чтобы в шарнирном четырехзвеннике не было слишком больших или слишком малых длин звеньев выбираем четыре положительных числа, удовлетворяющих условиям a < b < c < d, d/a ≤ m.
Второе ограничение – шарнирный механизм должен быть кривошипно-коромысловым, то есть должно выполняться условие ![]() .
.
Третье ограничение – угол давления на коромысло со стороны шатуна должен быть меньше допускаемого значения ![]() <
<![]() , где
, где ![]() .
.
Выбор метода оптимизации. Кинематические параметры четырехзвенного шарнирного механизма будем находить из условия минимума функции численным методом поиска с применением компьютерной техники, а выбор оптимального решения проводить с помощью целевой функции, определяемой выходными параметрами, чтобы сумма квадратов отклонении шатунной кривой точки М от заданной кривой (наклонного эллипса) была наименьшей от центра плоской фигуры. В данном случае отклонения подчиняются нормальному закону распределения, поэтому применение такого численного метода оптимизации позволяет выбрать оптимальные значения выходных параметров и достичь наилучшего варианта конструкции шарнирного четырехзвенника.
Алгоритм вычисления целевой функции. Как видно из рисунка 2, заданное кинематическое свойство механизма состоит в том, что точка М на шатуне шарнирного четырехзвенного механизма должна описывать траекторию, мало отличающуюся от заданной кривой – наклонного эллипса при произвольных координатах его центра (заданы большая полуось а1 и малая полуось b1, угол наклона большой оси ![]() ). Так как в данном случае целевая функция является неявной, составить ее в явном виде через искомые параметры синтеза не представляется возможным. Однако можно указать последовательность ее вычисления, то есть составить алгоритм вычисления, чтобы получить Δ (целевая функция) для данной комбинации параметров синтеза шарнирного четырехзвенника.
). Так как в данном случае целевая функция является неявной, составить ее в явном виде через искомые параметры синтеза не представляется возможным. Однако можно указать последовательность ее вычисления, то есть составить алгоритм вычисления, чтобы получить Δ (целевая функция) для данной комбинации параметров синтеза шарнирного четырехзвенника.
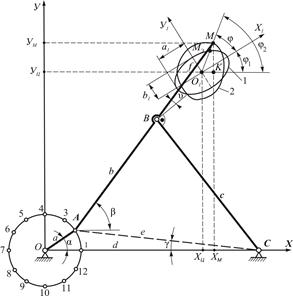
Рисунок 2. Схема плоского четырехзвенного шарнирного механизма. 1 – заданная траектория (наклонный эллипс) точки М на шатуне; 2 – траектория точки М на шатуне при произвольно выбранных выходных параметрах синтеза
Из ∆ ОАС находим диагональ АС шарнирно-рычажного четырехзвенного механизма
![]() . (1)
. (1)
Угол наклона диагонали АС равен
![]() . (2)
. (2)
Из ∆ АВС находим угол давления на коромысло ВС со стороны шатуна АВ, при условии, что сила, действующая на коромысло, направлена по оси шатуна
![]() . (3)
. (3)
Угол наклона шатуна АВ к стойке равен
![]() . (4)
. (4)
Проецируя контур ОАВМ на координатные оси составим выражения для нахождения искомых координат точки М
![]() , (5)
, (5)
![]() . (6)
. (6)
За один оборот кривошипа угол ![]() меняется от 0 до
меняется от 0 до ![]() . Разбиваем траекторию точки А на п равных частей, отсюда следует, что значение угла
. Разбиваем траекторию точки А на п равных частей, отсюда следует, что значение угла ![]() будет меняться через каждые ∆
будет меняться через каждые ∆![]() (рис. 1).
(рис. 1).
Тогда координаты центра плоской фигуры (шатунной кривой или наклонного эллипса), описываемой точкой М, равны
![]() ,
, ![]() . (7)
. (7)
После вычисления координат ![]() ,
, ![]() ,
, ![]() и
и ![]() шатунной кривой из ∆О1МК находим расстояние от центра эллипса
шатунной кривой из ∆О1МК находим расстояние от центра эллипса ![]() до точки М шатуна
до точки М шатуна
![]() . (8)
. (8)
Угол наклона радиуса ![]() к стойке равен
к стойке равен
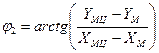 . (9)
. (9)
Тогда угол наклона радиуса ![]() к большой оси эллипса равен
к большой оси эллипса равен
![]() . (10)
. (10)
Расстояние от центра ![]() до соответствующей точки
до соответствующей точки ![]() эллипса (радиус эллипса в данной точке ) вычисляется по известной формуле
эллипса (радиус эллипса в данной точке ) вычисляется по известной формуле
![]() , (11)
, (11)
где: a1 – большая полуось эллипса;
b1 – малая полуось эллипса.
После вычисления расстояний ![]() и
и ![]() находим наиболее оптимальные искомые (выходные) параметры синтеза плоского шарнирного четырехзвенного механизма по методу наименьших квадратов, который основан на минимизации суммы квадратов невязок
находим наиболее оптимальные искомые (выходные) параметры синтеза плоского шарнирного четырехзвенного механизма по методу наименьших квадратов, который основан на минимизации суммы квадратов невязок
![]() . (12)
. (12)
Алгоритм оптимизации. После того, как составлен алгоритм вычисления целевой функции, производится поиск значений аргументов целевой функции, при которых она достигает минимума, чтобы получить оптимальные проектные параметры синтеза шарнирного четырехзвенника.
Порядок предлагаемой методики синтеза шарнирного четырехзвенника по заданной шатунной кривой в виде наклонного эллипса можно представить последовательностью следующих действий:
1. Учет исходных данных: расстояния между опорами d, большой полуоси а1 и малой полуоси b1, угла наклона большой оси ![]() эллипса к стойке.
эллипса к стойке.
2. Создание сетки в принятом диапазоне изменения аргументов целевой функции и узловых точек в ней, то есть разбиение диапазона на ряд отдельных значений, в которых необходимо вычислить целевую функцию с учетом условия a < b < c < d.
3. Учет второго ограничения в виде неравенства ![]() .
.
4. Учет третьего ограничения в виде неравенства ![]() <
<![]() .
.
5. Задание расчётных углов α на рассматриваемом участке вращения ведущего звена.
6. Вычисление значения целевой функции по предложенному выше алгоритму.
7. Определение искомых проектных длин звеньев механизма для комбинации найденного минимума целевой функции.
8. Рисование траектории точки М по найденным оптимальным проектным параметрам шарнирного четырехзвенника.
9. Рисование заданного наклонного эллипса.
8 и 9 пункты данного алгоритма дают возможность наглядно сравнить заданную и полученную траекторию движения точки М на шатуне.
Блок-схема разработанного алгоритма оптимизации проектных параметров механизма была представлена в [2, с. 15].
Полученные результаты. С помощью данной блок-схемы на алгоритмическом языке была разработана программа расчета проектных параметров шарнирного четырехзвенника, реализованная на персональном компьютере. Полученные значения параметров занесены в таблицу 1.
Таблица 1.
Проектные параметры четырехзвенного шарнирного механизма
|
Угол наклона заданного эллипса |
Выходные кинематические параметры, м |
Сумма квадратов невязок, м |
|||
|
|
|
|
|
|
|
|
π/6 |
0,18 |
0,79999 |
1,08999 |
0,46999 |
1,02·10-3 |
|
π/4 |
0,19 |
0,74999 |
1,00999 |
0,44999 |
4,9·10-4 |
|
π/3 |
0,19 |
0,79999 |
0,88999 |
0,42999 |
1,17·10-3 |
Причем, разработанная программа расчета стала пригодным для синтеза механизма по заданным шатунным кривым не только в виде наклонного эллипса, но и в виде окружности.
Оптимальные результаты расчета на ПК при ![]() π/4,
π/4, ![]() м,
м, ![]() м,
м, ![]() м и
м и ![]() м,
м, ![]() м с графическим изображением заданных и расчетных шатунных кривых приведены на рисунке 3, где а – длина кривошипа, b+f - длина шатуна, с – длина коромысла, hk – невязка, хмс и умс – координаты центра шатунной кривой.
м с графическим изображением заданных и расчетных шатунных кривых приведены на рисунке 3, где а – длина кривошипа, b+f - длина шатуна, с – длина коромысла, hk – невязка, хмс и умс – координаты центра шатунной кривой.


Рисунок 3. Расчетные параметры шарнирного четырехзвенника
Как видно из рисунка 3, разработанная программа расчета, реализованная на персональном компьютере, позволила достичь поставленной цели – приближенное воспроизведение траектории движения точки М на шатуне (шатунная кривая) в виде наклонного эллипса и окружности.
Планы положений звеньев механизма, построенные по вычисленным проектным параметрам синтеза, а также графики движения точки М, выстроенные по вычисленным координатам данной точки (по формулам 5 и 6) при соответствующих координатах центра шатунной кривой, представлены на рисунках 4 и 5.
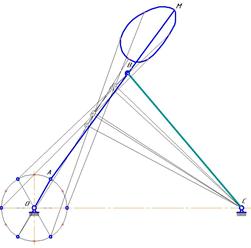
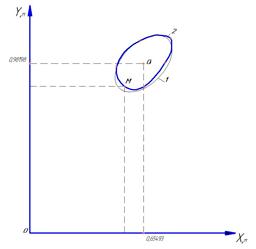
Рисунок 4. План положений механизма и график движения точки М. а =ОА=0,19 м; b=АВ=0,74999 м; с=ВС=1,00999 м; f =ВМ=0,44999 м; d=ОС=1, 2м; 1 – заданная шатунная кривая; 2 – расчетная шатунная кривая

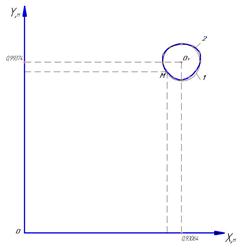
Рисунок 5. План положений механизма и график движения точки М. а= ОА=0,10999 м; b=АВ=0,69999 м; с=ВС=0,71999 м; f =ВМ=0,67 м, d=ОС=0,98 м; 1 – заданная шатунная кривая; 2 – расчетная шатунная кривая
Графическое изображение шатунной кривой, полученной при реализации на ПК разработанной программы расчета проектных параметров, и график шатунной кривой, построенной по координатам точки М, а также траектория движения, описываемой точкой М в плане положений механизма, совпали, что указывает на корректность и пригодность разработанной программы оптимизации проектных параметров четырехзвенного шарнирного механизма.
Оценка абсолютной и относительной погрешности вычисления. Важнейшей задачей синтеза приближенно-направляющих механизмов, помимо нахождения приближенной кривой линий, описываемой точкой шатуна, является оценка абсолютной и относительной погрешности.
В первом случае можно оценить погрешности приближения величины радиуса кривой, описываемой точкой М на шатуне, к величине радиуса заданного наклонного эллипса в соответствующей точке, а во втором случае, погрешности приближения величины радиуса кривой, описываемой точкой М на шатуне, к величине радиуса заданной окружности при различных углах поворота кривошипа. Тогда абсолютная погрешность определяется из выражения
![]() , (13)
, (13)
а относительная погрешность - из выражения
![]() . (14)
. (14)
Графики зависимости вычисленных по формулам (13) и (14) значения погрешностей от угла поворота кривошипа показаны на рисунке 6.
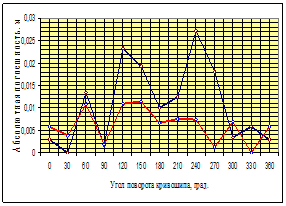
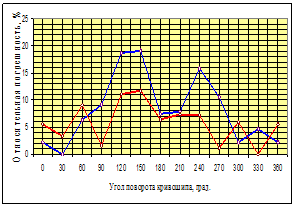
Рисунок 6. График зависимости абсолютной и относительной погрешности от угла поворота кривошипа
Средняя относительная погрешность приближения шатунной кривой к наклонному эллипсу или окружности не превышает 10 %, что указывает на оптимальность рассчитанных проектных параметров шарнирного четырехзвенника.
Вывод. Созданный программный продукт позволяет автоматизировать процесс проектирования шарнирно-рычажных четырехзвенных механизмов при воспроизводстве траекторий точки М на шатуне в виде кривой, приближенной к наклонному эллипсу или окружности.
Предложенная методика оптимизационного синтеза четырехзвенника, в отличие от существующих методик, предусматривает минимизацию отклонении точки расчетной шатунной кривой от центра плоской фигуры до соответствующей точки заданной шатунной кривой с использованием свойства эллипса, что существенно облегчает решение поставленной задачи и обеспечивает простоту и приемлемость для инженерных расчетов.
Список литературы:
1. Полак Э. Численные методы оптимизации: пер. с англ. Ф.И. Ерешко. – М.: Мир, 1974. – С. 376.
2. Бейсебаев А.К., Бейсенов Н.К. Синтез шарнирного четырехзвенника по заданной шатунной кривой // Вестник Карагандинского университета: математика. – 2014. Т. 75, № 3. – С. 11–16.
дипломов


Оставить комментарий