Статья опубликована в рамках: LII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 18 ноября 2015 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ФИНИТНОЕ УПРАВЛЕНИЕ СЕРВОПРИВОДАМИ СОЛНЕЧНЫХ МОДУЛЕЙ
Капля Егор Викторович
канд. физ.-мат. наук, доцент, ведущий научный сотрудник
филиала Московского энергетического института в г. Волжском,
РФ, г. Волжский
FINITE CONTROL BY THE SOLAR SERVO MODULES
Egor Kaplya
candidate of physics and mathematics, associate professor,
leading researcher branch of Moscow power engineering Institute in Volzhsky,
Russia, Volzhsky
Работа выполнена при поддержке проекта «Моделирование технологических процессов в системе объектов нетрадиционной и возобновляемой энергетики и оптимизация управления режимами совместной работы», выполняемого в рамках государственного задания Минобрнауки России.
АННОТАЦИЯ
Представлена новая структурная схема автоматизированного сервопривода солнечного модуля. Для поворота солнечного модуля использован сервопривод постоянного тока. Построены графики зависимости расхода энергии при финитном управлении серводвигателем от продолжительности поворота модуля. Оптимальная продолжительность поворота модуля соответствует минимуму энергетических затрат на процесс поворота.
ABSTRACT
Presents a new structural scheme of an automated servo solar module. For rotate the solar module used the DC servo motor. Graphs of the dependence of energy consumption at finite control by the solar servo on the duration of rotation. The optimal duration of rotation of the module corresponds to the minimum energy consumption for the turning process.
Ключевые слова: солнечный модуль; финитное управление; сервопривод; серводвигатель постоянного тока.
Keywords: solar module; finite control; fixed-time control; servo; servo-driver; DC servo motor.
Каждый модуль современных солнечных электростанций имеет индивидуальный сервопривод. Автоматическое позиционирование фотоэлектрических модулей, гелиостатов и параболоцилиндрических концентраторов обычно осуществляют с помощью электродвигателей. Для поворота солнечных модулей можно использовать сервопривод с двигателем постоянного тока (ДПТ), редуктором и энкодером. При угловом позиционировании солнечных модулей с помощью ДПТ целесообразно использовать систему финитного управления. Финитное управление реализуется на конечном отрезке времени [1, с. 13]. От продолжительности ![]() поворота модуля зависит количество затраченной энергии [2, с. 30].
поворота модуля зависит количество затраченной энергии [2, с. 30].
Поворот солнечного модуля вокруг горизонтальной и вертикальной осей предполагает использование двух серводвигателей. Алгоритмы управления двигателями аналогичны, поэтому рассмотрим систему позиционирования фотоэлектрического модуля при повороте вокруг одной горизонтальной оси ![]() (рис. 1). Начальное положение модуля характеризуется углом
(рис. 1). Начальное положение модуля характеризуется углом ![]() между вектором нормали к поверхности модуля и горизонтальной плоскостью. Необходимо повернуть модуль на угол
между вектором нормали к поверхности модуля и горизонтальной плоскостью. Необходимо повернуть модуль на угол ![]() с минимальными затратами энергии (рис. 2) и остановить его в положении с вектором нормали
с минимальными затратами энергии (рис. 2) и остановить его в положении с вектором нормали ![]() , направленным под углом
, направленным под углом ![]() относительно горизонтальной плоскости (рис. 1).
относительно горизонтальной плоскости (рис. 1).
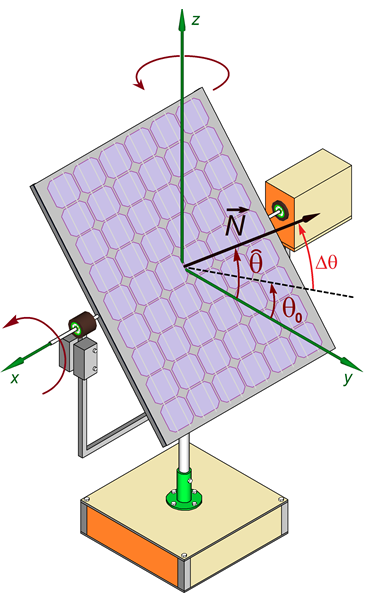
Рисунок 1. Система позиционирования фотоэлектрического солнечного модуля
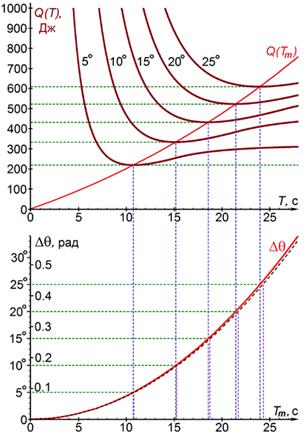
Рисунок 2. Графики зависимостей ![]() и
и ![]()
Структурная схема автоматизированного сервопривода постоянного тока с блоком финитного управления (БФУ) представлена на рис. 3.

Рисунок 3. Структурная схема автоматизированного сервопривода с блоком финитного управления
На схеме использованы следующие обозначения:
![]() – угол поворота солнечного модуля;
– угол поворота солнечного модуля; ![]() – угол поворота якоря ДПТ;
– угол поворота якоря ДПТ; ![]() – угловая скорость вала ДПТ;
– угловая скорость вала ДПТ; ![]() – угловая скорость солнечного модуля;
– угловая скорость солнечного модуля; ![]() – угловое ускорение солнечного модуля;
– угловое ускорение солнечного модуля; ![]() – угловое ускорение вала ДПТ;
– угловое ускорение вала ДПТ; ![]() – управляющее напряжение;
– управляющее напряжение; ![]() – ток в цепи якоря ДПТ;
– ток в цепи якоря ДПТ; ![]() – индуктивность цепи якоря;
– индуктивность цепи якоря; ![]() – активное сопротивление цепи якоря;
– активное сопротивление цепи якоря; ![]() – противодействующая ЭДС якоря;
– противодействующая ЭДС якоря; ![]() – коэффициент противоЭДС, связывающий
– коэффициент противоЭДС, связывающий ![]() с угловой скоростью;
с угловой скоростью; ![]() – вращающий момент, создаваемый ДПТ;
– вращающий момент, создаваемый ДПТ; ![]() – коэффициент пропорциональности, связывающий ток в цепи якоря и развиваемый двигателем вращающий момент;
– коэффициент пропорциональности, связывающий ток в цепи якоря и развиваемый двигателем вращающий момент; ![]() – момент сопротивления нагрузки, приведенный к валу двигателя;
– момент сопротивления нагрузки, приведенный к валу двигателя; ![]() – суммарный осевой момент инерции якоря ДПТ, колёс редуктора и солнечного модуля;
– суммарный осевой момент инерции якоря ДПТ, колёс редуктора и солнечного модуля; ![]() – передаточное число редуктора сервопривода.
– передаточное число редуктора сервопривода.
Жесткая механическая связь вала двигателя и вала нагрузки посредством зубчатых колес редуктора позволяет связать фазовые координаты: ![]() ;
; ![]() ;
; ![]() .
.
Измерение угла ![]() ориентации солнечного модуля осуществляется с помощью энкодера. Мгновенная угловая скорость
ориентации солнечного модуля осуществляется с помощью энкодера. Мгновенная угловая скорость ![]() и угловое ускорение
и угловое ускорение ![]() солнечного модуля вычисляются контроллером в результате численного дифференцирования функции
солнечного модуля вычисляются контроллером в результате численного дифференцирования функции ![]() по времени.
по времени.
На вход БФУ подаются заданные конечные значения фазовых координат вала солнечного модуля: ![]() ,
, ![]() ,
, ![]() , где
, где ![]() – момент времени начала поворота;
– момент времени начала поворота; ![]() – продолжительность поворота. Модуль переводится из одного неподвижного состояния в другое неподвижное состояние, поэтому начальную и конечную угловую скорость солнечного модуля примем равными нулю:
– продолжительность поворота. Модуль переводится из одного неподвижного состояния в другое неподвижное состояние, поэтому начальную и конечную угловую скорость солнечного модуля примем равными нулю: ![]() . Текущие значения фазовых координат сравниваются с заданными. БФУ вычисляет и формирует управляющий сигнал
. Текущие значения фазовых координат сравниваются с заданными. БФУ вычисляет и формирует управляющий сигнал ![]() на основе выбранного закона финитного управления.
на основе выбранного закона финитного управления.
Известный [1, с. 69] закон финитного управления при трех конечных условиях применительно к сервоприводу представим в следующем виде:
|
|
(1) |
где: ![]() – момент времени окончания переходного процесса;
– момент времени окончания переходного процесса;
![]() – жёсткость управления (временной интервал между ведущей и ведомой фазовыми точками);
– жёсткость управления (временной интервал между ведущей и ведомой фазовыми точками); ![]() ;
;
![]() – коэффициент пропорциональности между напряжением на обмотке ДПТ и угловым ускорением ротора;
– коэффициент пропорциональности между напряжением на обмотке ДПТ и угловым ускорением ротора; ![]() .
.
В основе математической модели сервопривода постоянного тока [4, с. 148] – система дифференциальных уравнений:
|
|
(2) |
|
|
(3) |
Момент сил сопротивления будем считать линейно зависящим от угловой скорости вращения ротора ДПТ:
|
|
(4) |
где: ![]() – момент трогания ротора двигателя и механической нагрузки сервопривода, приведенный к валу двигателя;
– момент трогания ротора двигателя и механической нагрузки сервопривода, приведенный к валу двигателя;
![]() – коэффициент сопротивления движению.
– коэффициент сопротивления движению.
Основной энергетической характеристикой процесса управления сервоприводом является величина электрической энергии ![]() , затраченной на питание ДПТ в процессе управления.
, затраченной на питание ДПТ в процессе управления.
Энергия, потребляемая якорем ДПТ от источника электрической энергии в процессе терминального управления сервоприводом, выражается интегралом:
|
|
(5) |
Ток в цепи якоря ДПТ представим решением уравнения (3) относительно ![]() :
:
|
|
(6) |
где ![]() – ток в цепи якоря в момент времени
– ток в цепи якоря в момент времени ![]() . При пуске двигателя можно принять
. При пуске двигателя можно принять ![]() , т. к. ток через индуктивный элемент не может измениться мгновенно.
, т. к. ток через индуктивный элемент не может измениться мгновенно.
Функция ![]() имеет минимум (рис. 3). Оптимальная продолжительность
имеет минимум (рис. 3). Оптимальная продолжительность ![]() поворота модуля соответствует минимуму целевой функции
поворота модуля соответствует минимуму целевой функции ![]() . При малых
. При малых ![]() требуются высокие напряжения (рис. 4).
требуются высокие напряжения (рис. 4).
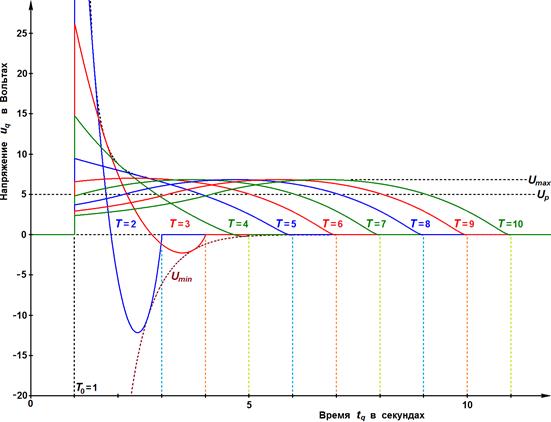
Рисунок 4. Форма управляющего сигнала при различных значениях ![]()
Величина ![]() зависит от заданных начальных и конечных условий, а также от характеристик сервопривода. В результате минимизации функции (5) при использовании управляющего сигнала (1) получена в [2, с. 30] формула:
зависит от заданных начальных и конечных условий, а также от характеристик сервопривода. В результате минимизации функции (5) при использовании управляющего сигнала (1) получена в [2, с. 30] формула:
|
|
(7) |
Формула (7) позволяет вычислить приближённое значение ![]() оптимальной продолжительности поворота модуля [3, с. 28] для заданного угла поворота
оптимальной продолжительности поворота модуля [3, с. 28] для заданного угла поворота ![]() представленного в радианах.
представленного в радианах.
Моделирование переходных процессов выполнено для сервопривода, обладающего характеристиками: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() при следующих начальных и конечных условиях:
при следующих начальных и конечных условиях: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ; приняты:
; приняты: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Графики зависимости энергии ![]() , затраченной в процессе поворота, от продолжительности
, затраченной в процессе поворота, от продолжительности ![]() поворота построены с помощью (1)–(6) при
поворота построены с помощью (1)–(6) при ![]() и показаны на рис.2. В результате минимизации функции
и показаны на рис.2. В результате минимизации функции ![]() для
для ![]() построен график зависимости
построен график зависимости ![]() , представленный в нижней части рис. 2 сплошной линией. Результаты расчёта
, представленный в нижней части рис. 2 сплошной линией. Результаты расчёта ![]() по формуле (9) представлены на рис. 2 наклонной пунктирной кривой. Близость сплошной и пунктирной расчётных кривых
по формуле (9) представлены на рис. 2 наклонной пунктирной кривой. Близость сплошной и пунктирной расчётных кривых ![]() подтверждает корректность расчёта оптимальной продолжительности поворота модуля с помощью формулы (9). Формула (9) позволяет найти оптимальную продолжительность процесса поворота солнечного модуля из одного неподвижного состояния в другое.
подтверждает корректность расчёта оптимальной продолжительности поворота модуля с помощью формулы (9). Формула (9) позволяет найти оптимальную продолжительность процесса поворота солнечного модуля из одного неподвижного состояния в другое.
Список литературы:
- Батенко А.П. Управление конечным состоянием движущихся объектов. – М.: Советское радио, 1977. – 256 с.
- Капля Е.В. Энергоэффективное терминальное управление серводвигателем постоянного тока // Автоматизация процессов управления. – 2015. – Т. 39, № 1. – С. 27–33.
- Капля Е.В. Энергоэффективное терминальное управление сервоприводами солнечных модулей // Альтернативная энергетика и экология. – 2015. – Т. 181–182, – № 17–18. – С. 24–29.
- Фираго Б.И., Павлячик Л.Б. Теория электропривода. – Мн.: ЗАО «Техноперспектива», 2004. – 527 с.
дипломов


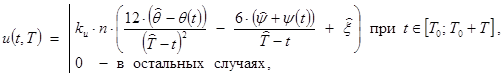
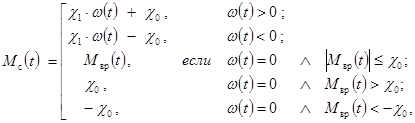
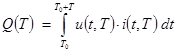 .
.
 .
.
Комментарии (1)
Оставить комментарий