Статья опубликована в рамках: XXV-XXVI Международной научно-практической конференции «Наука вчера, сегодня, завтра» (Россия, г. Новосибирск, 08 июля 2015 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ПОСТРОЕНИЕ МАТЕМАТИЧЕСКОЙ И ДИСКРЕТНОЙ МОДЕЛИ ОБЪЕКТА УПРАВЛЕНИЯ
Тимченко Ольга Викторовна
научный руководитель, канд. физ.-мат. наук, СКФУ, филиал, РФ, г. Пятигорск
E-mail: popeye125544@mail.ru
Джамалов Адиль Чубанович
студент 3 курса, инженерного факультета, Северо-Кавказский федеральный университет, филиал, РФ, г. Пятигорск
Пирмагомедов Олег Владимирович
студент 3 курса, инженерного факультета, Северо-Кавказский федеральный университет, филиал, РФ, г. Пятигорск
Чеченова Миранда Мирановна
студент 1 курса, экономического факультета, Северо-Кавказский федеральный университет, филиал, РФ, г. Пятигорск
Трегуб Александра Дмитриевна
студент 2 курса, инженерного факультета, Северо-Кавказский федеральный университет, филиал, РФ, г. Пятигорск
В данной работе рассмотрено построение математической модели теплопроводности пластины с конечными размерами.
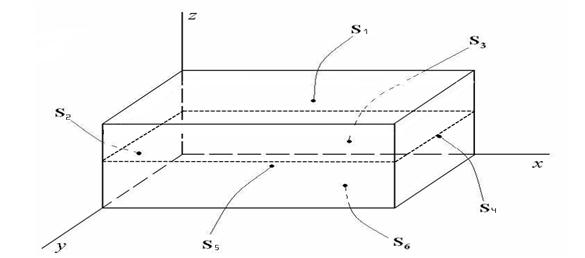
Рисунок 1. Физическая модель объекта
Параметры пластины приведены в таблице 1.
Таблица 1.
Начальные параметры пластины
|
Плоскость |
Граничные условия |
|
S1 |
T |
|
S2 |
0 |
|
S3 |
1 |
|
S4 |
0 |
|
S5 |
1 |
|
S6 |
0 |
где:
Т — входное воздействие в виде заданной температуры;
1 — температура поверхности равна 0;
0 — поверхность теплоизолированная.
Задана прямоугольная пластина c линейными размерами и величиной входного воздействия, вычисляемым по формулам:
![]() ;
;
![]() ;
;
![]() ;
;
![]() , где N =2
, где N =2
Математической моделью технологического процесса (объекта управления) называют систему математических отношений между входными и выходными параметрами процесса и конструктивными величинами, показателями качества, а также ограничения, накладываемые на параметры.
При изучении любого физического или другого какого-либо явления сначала получают качественное описание проблемы. На этапе моделирования качественное представление переходит в количественное. Одновременно определяют функциональные зависимости между переменными, и для каждого варианта входных данных находят выходные данные системы.
Для перехода от содержательного описания к математической модели необходимо:
1. провести декомпозицию объекта, разделив его на элементарные блоки, узлы, контуры, процессы, элементы и составить структурную схему объекта;
2. для каждого блока, элемента, контура составить уравнения, описывающие его поведение и определить математические соотношения между параметрами и показателями процесса;
3. записать все математические соотношения между элементами системы управления.
Для математического описания процессов, происходящих в объекте необходимо использовать:
· уравнения материального, теплового и энергетического баланса с учетом гидродинамики потоков и физических свойств жидкостей;
· ограничения на параметры процесса.
При построении математической модели используются:
1. алгебраические уравнения для описания статических, стационарных, режимов работы;
2. обыкновенные дифференциальные уравнения для описания динамических объектов с сосредоточенными параметрами или с распределенными параметрами;
3. дифференциальные уравнения в частных производных в случае описания статических моделей объектов с распределенными параметрами по нескольким координатам или для описания динамических нестационарных процессов объектов с распределенными параметрами [2, с. 63].
Уравнение, описывающее процесс распространения температуры в пластине запишем в виде
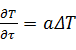 - Общий вид уравнения теплопроводности
- Общий вид уравнения теплопроводности
![]() (1)
(1)
уравнение теплопроводности для прямоугольной системы координат
где: 0 <x<Lx, 0 <y<Ly, 0 <z<Lz; a — коэффициент температуропроводности;
![]() — температурное поле пластины;
— температурное поле пластины;
τ — время.
Запишем граничные условия:
![]()
![]()
![]()
![]()
![]()
![]()
Пластина изготовлена из стали, поэтому для неё принимаем следующие значения: коэффициент температуропроводности а = 0,000019 м2/с.
Для реализации модели проведем дискретизацию (рис. 2). Разобьём пластину на зоны по всем трём пространственным координатам:
по оси X![]() с шагом дискретизации
с шагом дискретизации ![]() ;
;
по оси Y![]() с шагом дискретизации
с шагом дискретизации ![]() ;
;
по оси Z![]() с шагом дискретизации
с шагом дискретизации ![]() .
.
Шаг дискретизации по времени возьмём ![]() с.
с.
Определим линейные размеры пластины:
Lx = 0,01*2 = 0,02 м,
Ly = 0,02*0,4 = 0,008 м,
Lz = 0,02*0,2 = 0,004 м.
Шаги дискретизаций высчитаем по формулам:
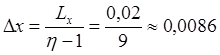 м,
м,
![]() м,
м,
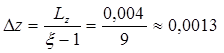 м.
м.
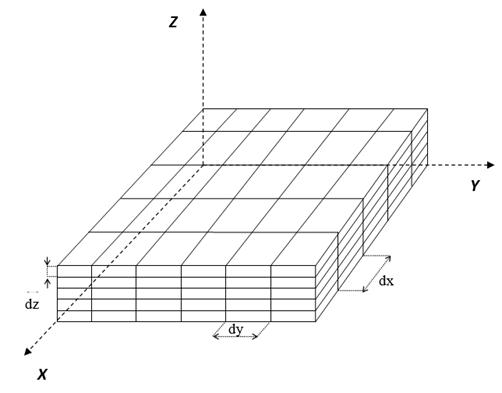
Рисунок 2. Дискретная модель пластины
Входное воздействие в виде заданной температуры ![]() . Тогда получим
. Тогда получим
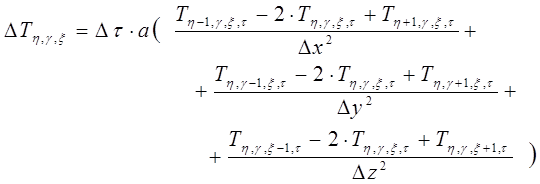 (2)
(2)
где: ![]() — разность температур в соседних точках через промежуток времени τ.
— разность температур в соседних точках через промежуток времени τ.
Температура в заданной точке вычисляется по формуле:
![]() .
.
Учитывая граничные условия, циклы для вычисления температуры по всем трём пространственным координатам будут иметь вид:
по оси X![]() ;
;
по оси Y![]() ;
;
по оси Z![]() .
.
График изменения температуры для точки с течением времени имеет вид (рис. 3):
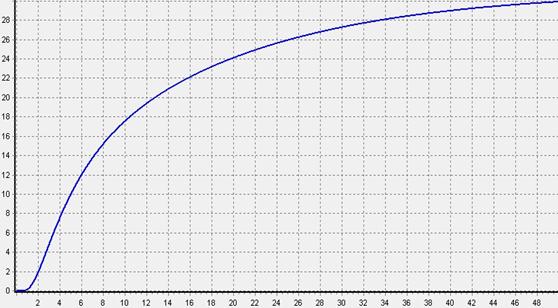
Рисунок 3. График изменения температуры пластины
В ходе работы была построена математическая модель нестационарного температурного поля внутри пластины заданных размеров. Для вычисления температурных полей можно выбрать императивный, структурированный, объектно- ориентированный язык Delphi, и среду разработки Embarcadero.
Список литературы: 1. Базаров И.П. Термодинамика / М.: Высшая школа, 1983. — 344 с.2. Боглаев Ю.П. Вычислительная математика и программирование / М.: Высш. Шк., 1990. — 544 с.3. Першин И.М Системы с распределенными параметрами. Анализ и синтез; М.: Научный мир, 2012. — 476 с.4. Сухарев М.В. Основы Delphi. Профессиональный подход; М.: Наука и техника, 2004. — 600 c.
дипломов


Оставить комментарий