ПРИМЕНЕНИЕ  МОДУЛЯРНОЙ  АРИФМЕТИКИ  В  СИСТЕМАХ  ОБРАБОТКИ  ИНФОРМАЦИИ

Иващенко  Виктория  Валерьевна

студент  4  курса  Полтавского  национального  технического  университета,  Украина,  г.  Полтава

E-mail: 

Черевко  Александр  Николаевич

канд.  техн.  наук,  зав.  кафедрой  теоретической  механики,  доцент  Полтавского  национального  технического  университета,  Украина,  г.  Полтава

E-mail: 

В  зависимости  от  способа  изображения  чисел  с  помощью  цифр  существующие  системы  счисления  условно  разделяют  на  позиционные  и  непозиционные.  Позиционная  система  счисления  —  это  такая  система  счисления,  в  которой  количественное  значение  каждой  цифры  разряда  зависит  от  ее  позиции  в  исходном  числе.  В  позиционной  системе  счисления  какое-либо  число  изображается  в  виде  последовательности  цифр  заданной  системы  счисления 

,

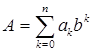где:    —  целые  числа, 

  —  разрядность  числа. 

При  этом  каждая  цифра  может  принимать  одно  из  возможных  значений  .  Количество    различных  цифр,  используемых  для  изображения  чисел  в  любых  позиционных  системах  счисления,  называются  основаниями    —  той  системы  счисления.  Так  для  десятичной  системы  счисления,  ,  а  для  двоичной  —  .

На  сегодняшний  день  основной  проблемой  построения  вычислительных  систем  остается  задача  обеспечения  ее  надежного,  отказоустойчивого  и  длительного  функционирования.  Особенно  эта  задача  актуальна  в  тех  отраслях,  в  которых  ошибка  или  сбой  работы  системы  могут  привести  к  ужасным  и  даже  непоправимым  последствиям,  таким,  к  примеру,  как  экологическая  катастрофа  или  человеческие  жертвы.  Методы  и  алгоритмы,  существующие  в  позиционных  системах  исчисления,  не  могут  полностью  обеспечить  эти  требования,  в  результате  этого  возникают  задачи  поиска  путей  совершенствования  систем  обработки  информации  путем  использования  нетрадиционных  систем  счисления.  Опираясь  на  исследования  специалистов  можно  сказать,  что  одним  из  перспективных  и  многообещающих  путей  решения  задачи  сокращения  времени  обработки  данных  и  повышения  надежности  вычислительных  средств  является  применение  различных  форм  параллельной  обработки  данных  в  том  числе  и  на  основе  числовых  систем  с  параллельной  структурой.  Одним  из  ведущих  направлений  среди  современных  подходов  к  созданию  отказоустойчивых  и  быстродействующих  средств  обработки  информации  является  использование  системы  остаточных  классов  или  как  ее  еще  называют  модулярная  система  счисления.

Модулярная  система  счисления  (СС)  (от  англ.  Residue  number  system)  —  это  непозиционная  система  счисления.  Представление  числа  в  данной  системе  основано  на  китайской  теореме  об  остатках,  а  операции  с  числами  выполняются  по  правилам  модульной  арифметики,  которая  используется  для  представления  больших  целых  чисел  в  виде  набора  небольших  целых  чисел  и  позволяет  оптимизировать  операции  с  большими  целыми  числами.

Преимуществами  модулярной  системы  счисления  есть:

1.  Высокая  скорость. 

Отсутствие  распространения  переноса  между  арифметическими  блоками  ведет  к  высокоскоростной  обработке  информации.

2.  Уменьшение  энергетических  затрат.

Использование  малых  арифметических  единиц  в  реализации  процессора  в  модулярной  системе  исчисления  уменьшает  количество  переключений  в  каждом  канале.  Это  в  свою  очередь  уменьшает  динамическую  мощность,  так  как  последняя  прямо  пропорциональна  переключающему  действию.

3.  Уменьшение  сложности.

Поскольку  представление  в  модулярной  системе  счисления  ведет  за  собой  преобразование  большого  числа  в  набор  остатков,  снижается  сложность  арифметических  единиц  в  каждом  модуле.  Это  облегчает  и  упрощает  общее  представление  чисел,  а  также  обнаружение  и  исправление  ошибок.  Так  как  модулярная  СС  не  является  позиционной  системой,  она  не  имеет  зависимости  между  каналами,  вследствие  чего  ошибка  в  одном  канале  не  распространяется  на  другие.  Изоляция  неисправных  остатков  повышает  отказоустойчивость  системы. 

Под  системой  остаточных  классов  (СОК)  понимают  такую  непозиционную  систему  счисления,  в  которой  целое  положительное  число    можно  представить  в  виде  набора  остатков  от  деления  этого  числа  на  выбранные  основы  (модули)  системы,  то  есть  ,  . 

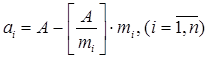Возможность  такого  представления  числа  определяется  теоремой  о  делении  с  остатком  в  кольце  целых  чисел  и  Китайской  теореме  об  остатках.

Зафиксируем  некоторое  число  ,  назовем  его  модулем.  Каждому  соответствует  определенный  остаток  от  деления  данного  числа  на  .  Назовем  два  числа    и    сопоставимыми  по  модулю,  если  при  делении  они  дают  одинаковый  остаток.  Это  записывается  в  виде:  .

Выполнение  сложения  и  умножения  выполняется  в  модулярной  арифметике  аналогично  тем  же  операциям  в  позиционной  системе  счисления  но  с  единственной  поправкой:  МСС  должна  содержать  достаточное  количество  допустимых  чисел  для  представления  результата  операции.  Если  данное  условие  не  выполняется,  говорится,  что  МСС  переполнена.  Это  означает  что  полученный  результат  имеет  более  одного  представления  чисел  в  реальной  системе  счисления.  Сумма  или  произведение,  которые  остаются  после  переполнения,  являются  корректной  суммой  по  отношению  к  модулю  численно  равному  числу  состояний  в  конечной  системе  счисления.  Соответствующие  цифры  должны  иметь  одинаковые  модули.  Модуль  результата  сложения  чисел  с  различными  модулями  в  основе  является  не  определенным.  Процесс  вычитания  в  МСС  осуществляется  основываясь  на  представлении  чисел  в  виде  дополнения,  которое  состоит  из  аддитивной  инверсии  относительно  положительных  чисел  в  МСС.  Аддитивная  инверсия  всегда  существует,  поскольку  каждое  число  в  МСС  является  элементом  поля.  Стоит  отметить,  что  отношение  между  остатком    и  его  аддитивной  инверсией    определяется  сравнением  .  Аддитивная  инверсия  может  быть  найдена  путем  использования  следующего  оператора  .

Процесс  деления  является  основным  препятствием  для  применения  МСС,  так  как  это  очень  трудоемкая  операция  по  двум  причинам: 

•      Отсутствие  мультипликативной  инверсии  для  0;

•      Соотношение  между  делением  в  МСС  и  в  нормальном  делении  возможно  лишь  в  случае,  когда  результат  арифметической  операции  является  целым  числом. 

Мультипликативная  инверсия    к  остатку    в  МА  определяется  сравнением  ,  где    существует  только  в  том  случае,  когда    и    взаимно  просты. 

Процесс  деления  традиционно  изображается  с  помощью  формулы:  ,  которую  можно  переписать  в  другом  виде,    где    -  это  знаменатель.

В  представлении  МСС  данная  операция  аналогична  сравнению  .  Умножив  обе  части  на  мультипликативную  инверсию    получим  .  В  случае,  когда  результат  операции  является  целым  числом,  получаем  результат  деления,  в  противном  случае  –  полученный  результат  не  будет  эквивалентным  делению  в  позиционной  системе  счисления.

Деление  в  МА  имеет  достаточно  интересные  свойства,  и  может  быть  использовано  для  решения  специфических  проблем,  но,  к  сожалению,  им  нельзя  заменить  процесс  нормального  деления.

Учитывая  то,  что  МА  является  не  позиционной  системой  счисления,  она  имеет  один  недостаток  —  невозможность  визуально  определить  величину  числа,  представленного  в  данной  СС.  Одним  из  путей  решения  данной  проблемы  есть  превращение  числа  с  МА  в  ПСС.  Существует  несколько  традиционных  методов  преобразования  чисел  с  МА  в  обобщенную  ПСС: 

•      метод  ортогональных  базисов;

•      метод  интервальных  оценок;

•      метод  с  использованием  коэффициентов  обобщенной  позиционной  системы  счисления.

В  целом,  конструирование  эффективных  схем  превращает  МА  в  узкоспециализированную  систему  счисления.

На  текущем  этапе  работы  можно  сказать,  что  МА  будет  эффективной  в  приложениях  и  программах,  где  необходимо  проводить  интенсивные  вычисления,  общей  арифметической  операцией  которых  будет  рекурсивное  сложение  и  умножение.  Достаточно  эффективно  применение  МА  в  таких  алгоритмах  как:  алгоритм  быстрого  преобразования,  преобразования  Фурье,  криптографических  алгоритмах  с  открытым  ключом  и  в  фильтрах  с  ограниченной  частотной  характеристикой. 

Применение  МА  также  будет  эффективным  в  той  области,  где  скорость  и  потребление  энергии  имеет  очень  важное  значение.  Особого  внимания  заслуживает  применение  МА  в  интегральных  схемах,  ведь  на  сегодняшний  день  данные  схемы  изготавливают  с  большой  плотностью,  где  провести  полное  тестирование  невозможно.  Благодаря  применению  МА  можно  избежать  распространения  ошибок  между  каналами,  а  поскольку  порядок  представления  остатков  не  важен,  остатки  с  ошибками  могут  быть  отброшены  и  исправлены  отдельно. 

Учитывая  изложенное,  можно  сделать  вывод,  что  МСС  является  весьма  важным  направлением  для  исследований,  в  связи  с  тем,  что  особенности  и  возможности  данной  системы  счисления  являются  востребованными  в  современных  вычислительных  алгоритмах.

Список  литературы:

1.Сиора  А.А.,  Краснобаев  В.А.,  Харченко  В.С.  Отказоустойчивые  системы  с  версионно-информационной  избыточностью/  Под  ред.  Харченко  В.С.;  ХАИ.  Харьков,  2009.  —  321  с.

2.Amos  Omondi,  Benjamin  Premkumar,  Residue  Number  Systems:  Theory  and  Implementation,  2007.  —  293  p.