Статья опубликована в рамках: XIII Международной научно-практической конференции «Наука вчера, сегодня, завтра» (Россия, г. Новосибирск, 09 июня 2014 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ДИССИПАТИВНОЕ ОТОБРАЖЕНИЕ ЦИЛИНДРА: НЕПОДВИЖНЫЕ ТОЧКИ КОЛЕБАТЕЛЬНОГО ТИПА
Лебедева Лариса Владимировна
канд. физ.-мат. наук, доцент ВГАВТ, РФ, г. Нижний Новгород
E -mail: Anoshina51@mail.ru
Отображение
|
|
(1) |
является математической моделью ряда радиофизических систем [2, с. 161; 3, с. 23; 5, с. 115]. Кроме того, это интересный математический объект [4, с 72; 6, с. 138]. Цель настоящей работы: установить области параметров, при которых отображение имеет в окрестности начала координат неподвижные точки, и определить характер устойчивости этих неподвижных точек.
1. Общие свойства отображения. Предположим, что параметры ![]() ,
, ![]() и
и ![]() отображения принадлежат области
отображения принадлежат области ![]() .
.
Очевидно [2, с. 16, 2] (в силу периодичности фазовых картин отображения по координате ![]() и симметричности фазового портрета в плоскости
и симметричности фазового портрета в плоскости ![]() относительно начала координат), что свойства отображения
относительно начала координат), что свойства отображения ![]() определяются свойствами отображения
определяются свойствами отображения 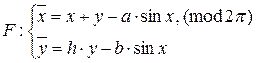 , являющегося отображением цилиндра
, являющегося отображением цилиндра ![]() на себя.
на себя.
Отличительной особенностью рассматриваемого отображения является наличие притягивающего слоя в его фазовом пространстве.
Теорема 1 . Любая траектория фазового пространства отображения (1) приходит в слой ![]() и не покидает его.
и не покидает его.
Доказательство . Приращение ![]() по переменной
по переменной ![]() имеет вид:
имеет вид: ![]() . Предположим, что
. Предположим, что ![]() . Тогда выполняется неравенство:
. Тогда выполняется неравенство: ![]() . Аналогично из неравенства
. Аналогично из неравенства ![]() следует неравенство
следует неравенство ![]() . Таким образом, траектории, начинающиеся вне слоя
. Таким образом, траектории, начинающиеся вне слоя ![]() (т. е. с координатами, удовлетворяющими условию:
(т. е. с координатами, удовлетворяющими условию: ![]() ), стремятся к слою
), стремятся к слою ![]() .
.
Докажем, что если точка с координатами ![]() принадлежит слою
принадлежит слою ![]() , то принадлежит слою
, то принадлежит слою ![]() и ее образ — точка с координатами
и ее образ — точка с координатами ![]() . Сначала рассмотрим случай
. Сначала рассмотрим случай ![]() . При этом справедливо неравенство
. При этом справедливо неравенство ![]() . Оценим разность
. Оценим разность ![]() . Имеем
. Имеем ![]() . Чтобы доказать, что при
. Чтобы доказать, что при ![]() справедливо неравенство
справедливо неравенство ![]() , оценим разность
, оценим разность ![]() . Очевидно, что она неотрицательна. Получили: если
. Очевидно, что она неотрицательна. Получили: если ![]() , то для всех
, то для всех ![]() точка с координатами
точка с координатами ![]() принадлежит слою
принадлежит слою ![]() . Аналогично рассматривается случай
. Аналогично рассматривается случай ![]() .
.
Теорема доказана.
Замечание 1. Утверждение теоремы справедливы не только в области параметров ![]() , но и для параметров из области
, но и для параметров из области ![]() .
.
Замечание 2. Если ![]() , то ширина притягивающего слоя — величина
, то ширина притягивающего слоя — величина ![]() — стремится к значению
— стремится к значению ![]() , а если
, а если ![]() , то эта величина неограниченно возрастает. Если
, то эта величина неограниченно возрастает. Если ![]() , то слой
, то слой ![]() — это весь цилиндр
— это весь цилиндр ![]() .
.
2. Неподвижные точки
Последовательность точек ![]()
![]() ...,
..., ![]() ,…, где
,…, где ![]() — точка с координатами
— точка с координатами ![]() ,
, ![]()
![]() и
и 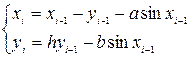 , назовем траекторией отображения
, назовем траекторией отображения ![]() . Будем говорить, что траектория является
. Будем говорить, что траектория является ![]() -циклом, если для ее точек верно соотношение: для
-циклом, если для ее точек верно соотношение: для ![]() выполнено, а для любого
выполнено, а для любого ![]() не выполнено условие
не выполнено условие ![]() . Неподвижной точкой типа
. Неподвижной точкой типа ![]() отображения
отображения ![]() назовем любую из точек
назовем любую из точек ![]() -цикла. При этом
-цикла. При этом ![]() соответствует циклу (неподвижной точке) вращательного (колебательного) типа. (Эти и другие используемые термины можно посмотреть в [1, с. 87].).
соответствует циклу (неподвижной точке) вращательного (колебательного) типа. (Эти и другие используемые термины можно посмотреть в [1, с. 87].).
2.1. Неподвижные точки типа ![]() .
.
Теорема 2 . Если параметры, принадлежат области ![]() , то отображение
, то отображение ![]() имеет неподвижные точки
имеет неподвижные точки ![]() и
и ![]() (и на цилиндре совпадающую с ней точку
(и на цилиндре совпадающую с ней точку ![]() ) типа
) типа ![]() . Неподвижная точка
. Неподвижная точка ![]() при всех значениях параметров — гиперболическая (седловая). Неподвижная точка
при всех значениях параметров — гиперболическая (седловая). Неподвижная точка ![]() устойчива в области
устойчива в области ![]() , где
, где ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() и неустойчива в области
и неустойчива в области ![]() .
.
Доказательство . Координаты неподвижных точек типа ![]() есть решения системы
есть решения системы  . Откуда и следует первая часть утверждения. Характеристическое уравнение [3, с. 82] системы (1) имеет вид:
. Откуда и следует первая часть утверждения. Характеристическое уравнение [3, с. 82] системы (1) имеет вид: ![]() , где
, где ![]() ,
, ![]() . Если
. Если ![]() , то при любых значениях параметров из области
, то при любых значениях параметров из области ![]() выполняется неравенство
выполняется неравенство ![]() . Таким образом, неподвижные точки
. Таким образом, неподвижные точки ![]() имеют гиперболический характер устойчивости [1, с. 95]. Если
имеют гиперболический характер устойчивости [1, с. 95]. Если ![]() , то
, то ![]() ,
, ![]() . Условие устойчивости в данном случае запишется как соотношение
. Условие устойчивости в данном случае запишется как соотношение ![]() . Поскольку при
. Поскольку при ![]() выполняется неравенство
выполняется неравенство ![]() , то в области
, то в области![]() точка
точка ![]() устойчива.
устойчива.
Следствие. Неподвижная точка ![]() теряет свою устойчивость либо при переходе через прямую
теряет свою устойчивость либо при переходе через прямую ![]() (в результате бифуркации удвоения, превращаясь в «обратное седло»), либо при переходе через прямую
(в результате бифуркации удвоения, превращаясь в «обратное седло»), либо при переходе через прямую ![]() (превращаясь в неустойчивый фокус или неустойчивый узел).
(превращаясь в неустойчивый фокус или неустойчивый узел).
2.2. Неподвижные точки типа ![]() .
.
Теорема 3 . При 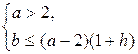 отображение
отображение ![]() имеет неподвижные точки
имеет неподвижные точки ![]() типа
типа ![]() , координаты которых суть решения системы:
, координаты которых суть решения системы:
|
|
(2) |
Кроме этих точек при ![]() отображение
отображение ![]() имеет неподвижные точки с координатами, определяемыми системой:
имеет неподвижные точки с координатами, определяемыми системой:
|
|
(3) |
Доказательство . Координаты неподвижных точек типа ![]() есть решения системы
есть решения системы 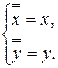 т.е. системы
т.е. системы 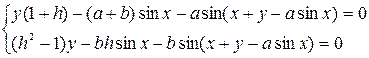 . Выполнив некоторые алгебраические преобразования системы, получим, что, если неподвижные точки типа
. Выполнив некоторые алгебраические преобразования системы, получим, что, если неподвижные точки типа ![]() существуют, то их координаты являются решениями системы:
существуют, то их координаты являются решениями системы:  , т.е . решением одной из двух систем:
, т.е . решением одной из двух систем:
|
А). |
или |
В). |
Решение системы А . Эта система может быть преобразована к виду:  Второе уравнение имеет решение на множестве
Второе уравнение имеет решение на множестве ![]() только при выполнении условия
только при выполнении условия ![]() (т. е. или
(т. е. или ![]() , или
, или ![]() ). Первое положение теоремы доказано.
). Первое положение теоремы доказано.
Решени системы В . Система может быть преобразована к виду: 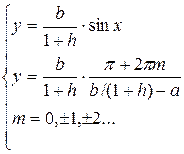 . Она имеет решение, если верно неравенство
. Она имеет решение, если верно неравенство 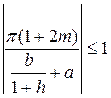 . Следовательно, необходимое
. Следовательно, необходимое
условие существования решения системы В — это истинность неравенства: ![]() . Соответствующее решение записывается в виде системы (3). Теорема доказана.
. Соответствующее решение записывается в виде системы (3). Теорема доказана.
Следствие 1 (обобщение следствия 1 из теоремы 2). При переходе через бифуркационную прямую ![]() неподвижная точка
неподвижная точка ![]() теряет свою устойчивость, и из нее рождается пара неподвижных точек, координаты которых есть решения системы (2).
теряет свою устойчивость, и из нее рождается пара неподвижных точек, координаты которых есть решения системы (2).
Замечание. Неподвижные точки вида (3) существуют только при ![]() , т. е. вне рассматриваемой области параметров
, т. е. вне рассматриваемой области параметров ![]() .
.
Теорема 4 . Неподвижные точки ![]() устойчивы, если выполнена одна из систем неравенств:
устойчивы, если выполнена одна из систем неравенств:
|
А. |
|
|
|
или |
|
В. |
|
Доказательство . Характеристическое уравнение отображения 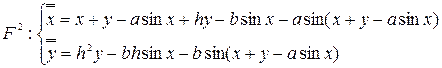 имеет вид:
имеет вид: ![]() , где (т.к.
, где (т.к. ![]() )
) ![]() ,
, ![]() . Чтобы неподвижная точка была устойчива, должны выполняться [3, с. 91] три неравенства
. Чтобы неподвижная точка была устойчива, должны выполняться [3, с. 91] три неравенства ![]() ,
, ![]() ,
, ![]() . Проанализируем их.
. Проанализируем их.
Рассматривая разность ![]() , установим, что, если истинно неравенство
, установим, что, если истинно неравенство 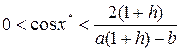 , то выполняется и соотношение
, то выполняется и соотношение ![]() .
.
Если ввести замену ![]() ,
, ![]() , то разность
, то разность ![]() можно записать в виде суммы двух квадратов
можно записать в виде суммы двух квадратов ![]()
![]() . Значит, в области
. Значит, в области ![]() неравенство
неравенство ![]() является верным.
является верным.
Условие ![]() , очевидно, записывается одной из двух систем неравенств.
, очевидно, записывается одной из двух систем неравенств.
Или в виде системы А.  , или в виде системы
, или в виде системы
В.  . Учитывая, что при
. Учитывая, что при ![]() неравенство
неравенство  справедливо, получаем доказательство теоремы.
справедливо, получаем доказательство теоремы.
Следствие . Неподвижные точки типа ![]() не имеют бифуркации удвоения.
не имеют бифуркации удвоения.
4. Заключение. Установлено существование области параметров, при которых отображение имеет устойчивую неподвижную точку или устойчивый ![]() -цикл. Значит, возможно глобально асимптотически устойчивое колебательное движение фазовых траекторий вблизи начала координат. Это важно с точки зрения работы реальных радиофизических систем [5, с. 197], математической моделью которых является рассматриваемое отображение.
-цикл. Значит, возможно глобально асимптотически устойчивое колебательное движение фазовых траекторий вблизи начала координат. Это важно с точки зрения работы реальных радиофизических систем [5, с. 197], математической моделью которых является рассматриваемое отображение.
Список литературы:
1.Арнольд В.И. Дополнительные главы теории обыкновенных дифференциальных уравнений. М., Наука, 1978.
2.Белых В.Н. Модели дискретных СФС и их исследование. В кн. Системы фазовой синхронизации // Под ред. В.В. Шахгильдяна, Л.Н. Белюстиной. М.: Радио и связь, 1982, — с. 161—162.
3.Белых В.Н Качественные методы теории нелинейных колебаний сосредоточенных систем. Учебное пособие. Горький, ГГУ, 1980.
4.Лебедева Л.В. Динамика импульсных систем фазовой синхронизации второго порядка // Сб. тез. Всесоюзной конф. «Развитие и совершенствование устройств синхронизации в системах связи». М. 1988.
5.Шахгильдян В.В., Ляховкин А.А. Системы фазовой автоподстройки частоты с элементами дискретизации. М.: Связь, 1979.
6.Lebedeva L.V. Bifurcation Sequence of One Cylinder Map // International Conference on CONTEMPORARY PROBLEMS in THEORY of DYNAMICAL SYSTEMS (CPTDS 96) Abstracts, Nizhny Novgorod, Russia, 1996.
дипломов


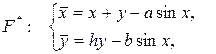
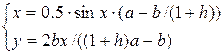

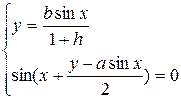
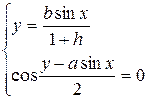


Оставить комментарий