Статья опубликована в рамках: XI Международной научно-практической конференции «Наука вчера, сегодня, завтра» (Россия, г. Новосибирск, 07 апреля 2014 г.)
Наука: Математика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
СОУДАРЕНИЕ ДВУХ АБСОЛЮТНО ЖЕСТКИХ ТЕЛ С УПРУГИМ ПРОМЕЖУТОЧНЫМ ЭЛЕМЕНТОМ, ИМЕЮЩИМ НЕЛИНЕЙНУЮ ХАРАКТЕРИСТИКУ
Попелло Егор Сергеевич
студент Оренбургского государственного университета, РФ, г. Оренбург
Е-mail : mouse-ka001@mail.ru
Кудина Лариса Ивановна
доцент Оренбургского государственного университета, РФ, г. Оренбург
Трактовки понятия удара различны. Но все они имеют общие характерные черты, а именно: относительную скорость тел к моменту их соприкосновения и наличие процесса перехода кинетической энергии в потенциальную энергию деформации. Таким образом, механическим ударом называется явление, возникающее при столкновении тел, сопровождающееся полным или частичным переходом кинетической энергии тел в энергию их деформации. Формулы классической теории удара успешно применяются в том случае, если время удара ![]() в несколько (3—5) раз превышает наибольший период собственных колебаний соударяющихся тел Т. Однако в формулы классической теории удара время не входит. Кроме того, с помощью этих формул нельзя рассчитать силу удара, напряжение в соударяющихся телах, их перемещения и ускорения. Для их определения приходиться комбинировать методы классической механики удара с элементами теории упругости [1, с. 5].
в несколько (3—5) раз превышает наибольший период собственных колебаний соударяющихся тел Т. Однако в формулы классической теории удара время не входит. Кроме того, с помощью этих формул нельзя рассчитать силу удара, напряжение в соударяющихся телах, их перемещения и ускорения. Для их определения приходиться комбинировать методы классической механики удара с элементами теории упругости [1, с. 5].
Рассмотрим ударную систему, у которой промежуточный элемент настолько мягок, а соударяющиеся тела настолько жесткие, что деформацией соударяющихся тел можно пренебречь, учитывая лишь деформацию промежуточного упругого элемента. Положение, показанное на рисунке пунктиром, соответствует моменту касания упругим элементом ударяемого тела — началу удара [2, c. 50].
Из рисунка (рисунок 1) очевидны равенства (1) и (2):
![]() =
= ![]() (1)
(1)
α= ![]() – l =
– l =![]() (2)
(2)
где: α — сжатие промежуточного элемента;
![]() — длина промежуточного элемента после во время удара;
— длина промежуточного элемента после во время удара;
![]() — длина пружины до удара;
— длина пружины до удара;
![]() перемещение центров тяжести тел соответственно [2, c. 60].
перемещение центров тяжести тел соответственно [2, c. 60].
Сила сопротивления сжатию упругого элемента N зависит от его конструкции
N = f(α) (3)
f(α) = cα (4)
Сила сжатия упругого элемента действует на оба тела, сообщая им ускорения. Следствии этого скорость центров тяжести тел изменится и после удара будет иметь значение: для ударника, для ударяемого тела:
![]() (5)
(5)
![]() . (6)
. (6)

Рисунок 1. Процесс деформации упругого элемента при ударе
|
Обозначим соответственно ускорения ударника и ударяемого тела.
![]() (7)
(7)
![]() (8)
(8)
За положительное направление сил, скоростей, ускорений примем направление первоначальных перемещений. Тогда дифференциальное уравнение движения тел получат вид :
![]() (9)
(9)
![]() (10)
(10)
Принимая для простоты, что ударяемое тело до удара было неподвижно, а упругий элемент не имел начального сжатия, присоединяя к дифференциальным уравнения движения тел, получим систему дифференциальных уравнений:
![]() (11)
(11)
![]() (12)
(12)
![]()
N = f(α) ![]()
t=0 ![]()
![]() =
=![]() =0 α =0 N = 0
=0 α =0 N = 0
![]() :
:
![]() (13)
(13)
![]() (14)
(14)
Исключая интеграл силы по времени, находим:
![]() =
=![]() (15)
(15)
![]() =
=![]() (16)
(16)
Дифференцируем уравнения по времени и делаем подстановки, преобразования. Откуда получаем зависимость сжатия тел α по времени:
t=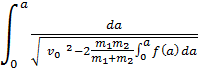 (17)
(17)
Максимальному сближению тел во время удара ![]() соответствует условие экстремума da/dt=0. В этом случае:
соответствует условие экстремума da/dt=0. В этом случае:
![]() =
=![]() (18)
(18)
![]() (19)
(19)
A п — часть кинетической энергии ударника, которая в процессе удара переходит в потенциальную энергию. Находим время соответствующее максимальному сжатию :
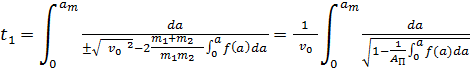 (20)
(20)
Таким образом полное время удара:
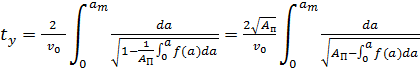 =
=
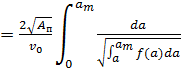 (21)
(21)
Максимальную сила удара будет соответствуем наибольшему сжатию упругого элемента, т. е.
![]() =f(
=f(![]() ) (22)
) (22)
Наибольшие ускорения соответствуют наибольшей силе.
![]() (23)
(23)
![]() (24)
(24)
Рассмотрим случай, когда упругий элемент имеет нелинейную характеристику.
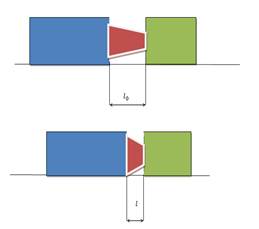
Рисунок 2. Процесс деформации упругого элемента при ударе
Рассмотрим наиболее общий случай, когда силы упругости элемента не линейны его деформации, а изменяются по степенному закону (рисунок 2). Величина ударной силы будет равна:
![]() , (25)
, (25)
где: ![]() — условный коэффициент жесткости упругого элемента, Н/мn;
— условный коэффициент жесткости упругого элемента, Н/мn;
a — деформация упругого элемента, м;
![]() — показатель степени.
— показатель степени.
Максимальная ударная сила будет соответствовать наибольшему сжатию упругого элемента.
Определим работу, совершаемую ударной силой:
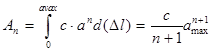 , (26)
, (26)
где: ![]() — максимальная абсолютная деформация упругого элемента, м.
— максимальная абсолютная деформация упругого элемента, м.
Работа ударной силы будет равна потенциальной энергии деформированного упругого элемента A:
![]() , (27)
, (27)
где ![]() ,
, ![]() — массы тел соответственно, кг;
— массы тел соответственно, кг;
![]() — относительная скорость тел в момент начала удара, м/с.
— относительная скорость тел в момент начала удара, м/с.
Приравнивая выражения (26) и (27), выразим максимальную абсолютную деформацию.
 . (28)
. (28)
После подстановки выражения (28) в формулу (25) можно получить максимальную ударную силу и максимальные ускорения тел ![]() и
и ![]() .
.
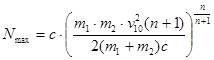 , (29)
, (29)
![]() , (30)
, (30)
![]() . (31)
. (31)
Построим график зависимости ударной силы от степени n (рисунок 3).
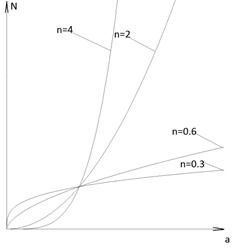
Рисунок 3. График зависимости ударной силы от степени n
По построенному графику можно сделать вывод: чем меньше степень n, тем меньше N, следовательно, меньше динамические нагрузки на соударяемые тела.
Практическое применение данной работы, заключается в следующем. Промежуточный элемент с нелинейными характеристиками может иметь широкий спектр применения, так как эффективнее справляется с гашением динамических нагрузок, нежели элемент с линейной зависимостью.
Данный промежуточный элемент может применяться:
· для обеспечения пассивной безопасности автомобиля при столкновениях;
· как элемент обшивки речного транспорта для более безопасной швартовки в портах;
· как подушка конечного торможения скоростного лифта;
· в других случаях, когда имеется ударная нагрузка.
Список литературы:
1.Александров Е.В., Соколинский В.Б. Прикладная теория и расчеты ударных систем / Е.В. Александров, В.Б. Соколинский. М.: Наука, 1969. — 199 с.
2.Власов Ю.Л. Удар. Общие рекомендации по решению задач: методические указания к практическим занятиям по дисциплине «Теоретическая механика»/ Ю.Л. Власов. Оренбург: ОГУ, 2010. — 36 c.
дипломов


Оставить комментарий