ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКОЙ КОМПЕТЕНЦИИ УЧАЩИХСЯ В ПРОЦЕССЕ РЕШЕНИЯ СТОХАСТИЧЕСКИХ ЗАДАЧ

Блинова Татьяна Леонидовна

канд. пед. наук, доцент УрГПУ,

 г. Екатеринбург

E-mail: 

Демократизация и гуманизация российского общества, активизация социальных и экономических отношений привели к появлению новых требований к результатам образования. Традиционные общеобразовательные цели дополняются новыми — формированием высокого уровня компетентности выпускников школ. Одним из основных направлений реализации поставленных целей является расширение познавательно-мотивационной сферы деятельности учащихся, что невозможно без формирования у них предметной компетенции.

В соответствии с разделением содержания образования на общее метапредметное (для всех предметов), межпредметное (для цикла предметов или образовательных областей) и предметное (для каждого учебного предмета), компетенции выстраиваются три уровня:

1. ключевые компетенции — относятся к общему (метапредметному) содержанию образования;
2. общепредметные компетенции — относятся к определенному кругу учебных предметов и образовательных областей;
3. предметные компетенции— частные по отношению к двум предыдущим уровням компетенции, имеющие конкретное описание и возможность формирования в рамках учебных предметов [2].

Анализ возможностей использования в процессе обучения стохастических задач позволил выделить умения, формируемые в процессе их решения, необходимые для формирования математической компетенции:

• умение формулировать проблему, выдвигать и доказывать гипотезу, критически анализировать результат. Постановка проблемы на «открытие» новых знаний возможна при проведении опыта обобщения результатов решения задач;
• умение производить наблюдение математических объектов и сравнивать результаты наблюдений, проводить математический эксперимент (выполнять вычисления, построения, измерения, моделировать объекты);
• умение выявлять связи между объектами задачи и их свойствами, связи между полученными связями, умение находить дополнительные элементы в задаче, связи между ними и данными элементами тесно связаны с приёмами «синтез», «анализ», «сравнение». Особенно роль анализа значима при формировании второго умения, так как практика показывает, что увидеть нужные дополнительные элементы задачи могут не все учащиеся. Овладевая этими умениями, школьники накапливают опыт отбора необходимой информации для решения задачи, синтезируют всю информацию об объектах;
• умение разбивать задачу на подзадачи, где учащиеся могут свести исходную задачу к решению более простых задач или задач, решение которых им известно. Адаптация известной информации к решаемой задаче является показателем организации мыслительной деятельности учащихся;
• умение находить различные способы решения задачи, которое способствует более глубокому освоению учащимися знаний, формированию действия контроля и оценки. Обсуждая направление возможных путей решения задачи, школьники становятся соучастниками познавательного и научного поиска;
• умение составлять взаимно-обратные задачи, обобщать задачу. При этом происходит не только систематизация знаний, но возникает желание составлять новые исследовательские задачи, что выводит учеников на новый виток знаний.

Основная эвристическая деятельность учащихся в учебном исследовании связана с выдвижением гипотезы, так как проблема чаще всего формулируется самим учителем, а доказательство или опровержение гипотезы сводится к доказательству соответствующей теоремы.

В зависимости от способа выдвижения гипотезы Е.В. Баранова выделяет следующие виды учебных исследований [1]:

а) интуитивно-опытные;

б) опытно-индуктивные;

в) индуктивные;

г) дедуктивные.

Реализация данных видов учебных исследований при решении стохастических задач будут в полной мере содействовать формированию математической компетенции.

Каждый вид учебного исследования связан с раскрытием новых математических фактов. Причем открытию нового материала может способствовать каждый из указанных видов, а для углубления знаний учащихся, т. е. получения дополнительных математических сведений более целесообразно использовать индуктивные и дедуктивные учебные исследования. В процессе выполнения дедуктивных учебных исследований осуществляется также и систематизация изученных школьниками знаний.

В обучении стохастике особое значение приобретает исследовательская деятельность учащихся при решении задач. В процессе работы над задачей учащиеся учатся самостоятельно выделять главные и вспомогательные объекты, анализировать отобранную информацию, обобщать и систематизировать ее, открывать, а затем использовать алгоритмы решения математических задач, овладевать определенной системой эвристик, находить наиболее рациональные приемы решения задач, критически осмысливать полученные результаты и применять их в дальнейшем.

Приведем пример организации решения исследовательской стохастической задачи, направленной на формирование математической компетенции учащихся:

Задача: экспериментально определить частоту выпадения орла при подбрасывании монеты.

1 этап

Приготовьте монету (одну на двух учащихся, сидящих за одной партой). Чтобы определить, как часто при бросании монеты выпадает орел, будем подбрасывать монету и фиксировать число выпадений орла. Если выпал орел — ставьте черточку в первой строке, если решка — во второй строке. Чтобы работа шла быстро, один ученик из пары бросает монету и называет выпавшую сторону, а второй вписывает черточки в таблицу 1.

Таблица 1

Бросьте монету 40 раз и заполните таблицу 1.

2 этап

1. заполните последний столбец таблицы 1, определив частоту выпадения орла по формуле (все числа округлите до сотых):

2.

В данном эксперименте знаменатель во всех вычислениях равен 40 — общему числу бросков, а в числитель подставьте числа, полученные в опыте.

3.предположите, какая теоретически должна быть частота выпадения орла при бросании монеты?____________________ Почему? _____________________________________________________________ _____________________________________________________________

4.сравните свои экспериментально полученные результаты с предполагаемым:___________________________________________________________________________________________________________

5.как можно найти частоту появления решки в данном эксперименте? (Укажите два способа!) _______________________________________________________________________________________________________________________________________________________________________________________

3 этап

Обсудим результаты работы всего класса.

1.сколько пар учащихся получили в результате частоту ровно 0,5? ________________

2.сколько пар учащихся получили частоту большую 0,5? _________________

3.сколько пар учащихся получили частоту меньшую 0,5? ________________

4.сравните число ответов на два предыдущих вопроса 2) и 3) ______________________

5.объясните результат, полученный в пункте 4 __________________________________________________________________________________________________________________________

4 этап

Обобщим полученные результаты.

Каждая пара бросила монету лишь 40 раз. Если мы объединим результаты бросков всего класса, то получим во много раз большее число опытов. (Например, если в классе присутствует 20 человек, то они образовали 10 пар и сделали 400 бросков).

Поочередно сообщая свои результаты, заполните таблицу 2 (кроме последнего столбца). Найдите и впишите в ячейку последнего столбца общее количество выпавших орлов, сложив числа, названные отдельными парами.

Найдите общее число бросков и найдите частоту выпадения орла при общем числе бросков.

Таблица 2

Результаты, полученные разными группами учеников

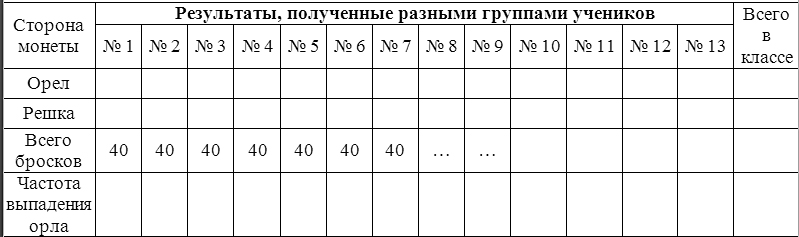
В целом по классу частота выпадения орла получилась равной ___________________

1.Зависит ли полученный результат от длины серии эксперимента (количества бросков)? _____________ Стал ли «общий» результат ближе к 0,5, по сравнению с результатами отдельных учащихся? ______________________________________________

2.Предположите, сколько раз мы можем ожидать выпадение орла, если сделать 10000 бросков монеты? ________________________________ А если сделать 24 000 бросков? ___________ При 4040 бросках монеты? ___________

Сделайте общий вывод.

Таким образом, можно сделать вывод, что использование в процессе обучения математике задач такого типа в полной мере способствует формированию соответствующей предметной компетенции.

Список литературы:

1. Баранова Е.В. Как увлечь школьников исследовательской деятельностью // Математика в школе. — 2004. — № 2. — С. 3—5.
2. Хуторской А.В. Технология проектирования ключевых и предметных компетенций // Интернет-журнал «Эйдос». — 2005. — 12 декабря. http://www.eidos.ru/journal/2005/1212.htm