ПОИСК И УСТРАНЕНИЕ ВЫБРОСОВ И СХОЖИХ ЭЛЕМЕНТОВ ВЫБОРКИ В ЗАДАЧЕ ВОССТАНОВЛЕНИЯ ФУНКЦИИ ПО ЭКСПЕРИМЕНТАЛЬНЫМ ДАННЫМ

Копылов Иван Владимирович

аспирант, Череповецкий государственный университет,

РФ, г. Череповец

E-mail: ivv.kopylov@gmail.com

Царев Владимир Александрович

канд. техн. наук, генеральный директор ООО «Малленом Системс»,

РФ, г. Череповец

E-mail: tsarev@mallenom.ru

SEARCH AND ELIMINATION OF NOISE AND SIMILAR ELEMENTS WHEN RESTORING FUNCTION ON THE EXPERIMENTAL DATA

Ivan Kopylov

postgraduate student, Cherepovets State University,

Russia, Cherepovets

Vladimir Tsarev

ph.D., Chief Executive Officer at “Mallenom Systems” company,

Russia, Cherepovets

АННОТАЦИЯ

В данной статье исследуется метод машинного обучения, основанный на теории случайных функций. Показано, что для данного метода существует быстрый способ обнаружения шумовых данных в обучающей выборке, а также схожих элементов, которые незначительно влияют на результирующий вид обученной «модели». Под «моделью» понимается построенная по обучающим данным интерполирующая или аппроксимирующая функция.

ABSTRACT

We investigate machine learning method based on the theory of random functions. This paper shows a quick method of detecting noise data and similar items in the training set. The similar items have a little effect on the resulting type of learning “model”. The term 'model' means interpolating or approximating function constructed from the training data. 

Ключевые слова: машинное обучение; интерполяция; аппроксимация; случайные функции; шумовые данные.

Keywords: machine learning; interpolation; approximation; random functions; noise data.

Введение.

Одним из эффективных вариантов решения задач многомерной интерполяции и аппроксимации является использование теории случайных функций. Предложенное в [1; 3] решение можно рассматривать как метод машинного обучения с учителем в признаковом пространстве, гарантирующий получение оптимального результата с точки зрения рассматриваемого математического аппарата теории случайных функций.

В данном методе машинного обучения – многомерная интерполяция и аппроксимация на основе теории случайных функций – искомая функция (обученная «модель») является наиболее вероятной реализацией случайной функции и выглядит следующим образом:

              (1)

где:  некая функция, характеризующая зависимость ожидаемого различия между значениями функции  в некоторых двух точках от расположения этих точек; коэффициенты ) находятся при обучении «модели» на эмпирических данных.

Последовательность  и соответствующие им  - представляют собой обучающую выборку.

Зачастую в обучающих данных присутствуют ложные элементы, или выбросы, а также элементы слабо влияющие на итоговый вид обученной «модели».

Рассматриваемый метод без особых затрат способен выявить лишние элементы в выборке. Математический аппарат метода позволяет провести процедуру кросс-валидации по отдельным объектам выборки без необходимости постоянного переобучения «модели» [2; 4; 5]. При сравнении значений функции (1) , полученной при обучении на эмпирических данных без элемента , с действительными значениями  возможно построить распределение отклонений между сравниваемыми значениями. По характеристикам распределения таким как математическое ожидание и среднеквадратическое отклонение возможно обнаружение шума в выборке, а также элементы, оказывающие допустимо малое воздействие на вид обученной «модели».

Кросс-валидация по отдельным объектам выборки.

Во многих случаях необходимо провести оценку качества обобщающих способностей построенной «модели». Процесс оценки представляет собой сравнение оцененных значений  с действительными известными значениями  (рис. 1). Этот процесс называется валидацией метода.

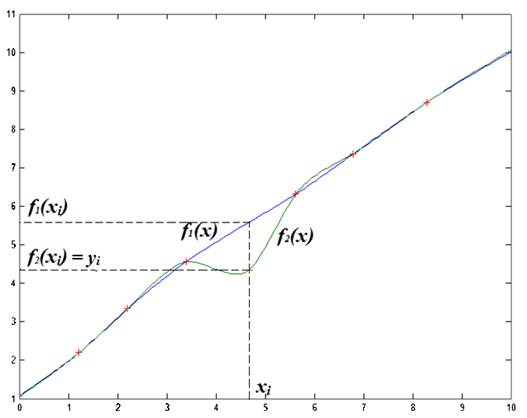
Рисунок 1. Графики вариантов функции , полученной при обучении на всех элементах обучающей выборки (функция ) и без  элемента (функция ). Разница  показывает величину отклонения функции от реального значения в случае, когда  элемент не участвовал в обучении

Кросс-валидация (cross-validation) позволяет проводить анализ «модели», используя только обучающие данные [4; 5]. При этом оценка обобщающих способностей полученной на этих же данных функции является несмещенной. Суть такого подхода заключается в том, что для  элементов обучающей выборки строится столько же вариантов аппроксимирующей функции . При получении вида -го варианта функции , где , используются все элементы обучающей выборки, кроме . В результате, при оценке обобщающих способней, сравниваются значения  и ,

Проведение подобного процесса оценки качества «модели» является достаточно дорогой процедурой с точки зрения затрат времени на вычисления, т. к. приходится строить «модель» заново ровно столько раз, сколько обучающих данных.

В статье [2] было показано, что в рамках рассматриваемого метода можно провести оценку обобщающих способностей обученной «модели» с помощью процедуры скользящего контроля leave-one-out cross-validation [4; 5] без необходимости постоянного проведения дорогостоящей процедуры переобучения. Полученная оценка качества будет в точности такая же, как если процедуру поэлементной валидации проводили с постоянным обучением «модели» заново при каждом удалении -го элемента из обучающей выборки.

Удаление выбросов и схожих элементов выборки.

При проведении поэлементной процедуры кросс-валидации возможно построить распределение отклонений значений функции (1)  в удаляемых – их элементах от известных значений .

По характеристикам распределения, таким как математическое ожидание и среднеквадратическое отклонение, возможно выявить шум в выборке, а также элементы, оказывающие допустимо малое воздействие на вид обученной «модели» (рис. 2).

Рисунок 2. Закрашенные красным цветом точки (ромбы) – выбросы, зеленым (кружки) – схожие элементы обучающей выборки. Красным цветом (пунктир) показан график функции (1), полученной при обучении на всех данных, включая шумовые. Синим цветом показан график функции, полученной при обучении без шумовых и схожих элементов выборки

Заключение.

В данной статье показано, что за счет особенностей математического аппарата метода машинного обучения, основанного на теории случайных функций, возможно быстрым способом обнаружить шумовые элементы в обучающей выборке, а также схожие элементы, которые незначительно влияют на результирующий вид обученной «модели». Это позволяет получить наиболее подходящий вид аппроксимирующей функции (1), а также сократить количество её слагаемых.

Список литературы:

1.    Бахвалов Ю.Н., Зуев А.Н., Ширабакина Т.А. Метод распознавания образов на основе теории случайных функций. – Санкт Петербург: Известия вузов. Приборостроение, 2005. Т. 48, № 2. С. 5–8. 

2.    Бахвалов Ю.Н, Копылов И.В. Обучение и оценка обобщающей способности методов интерполяции. – Ижевск: Компьютерные исследования и моделирование, 2015, Т. 5, № 5. С. 1023–1031. 

3.    Бахвалов Ю.Н., Малыгин Л.Л., Черкас П.С. Метод машинного обучения на основе алгоритма многомерной интерполяции и аппроксимации случайных функций. Вестник Череповецкого государственного университета 2012. – 2012, № 2, Т. 2. – С. 7–9.

4.    Скользящий контроль – [Электронный ресурс] – Режим доступа. – URL: http://www.machinelearning.ru/wiki/index.php?title=Кросс-валидация (Дата обращения 03.01.2016).

5.    Ron Kohavi. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. Computer Science Department, Stanford University, 1995, Р. 2–3.