ВЫБОР МЕТОДА УТОЧНЕНИЯ КОРНЕЙ С ПРИМЕНЕНИЕМ ПРОГРАММНОГО ПРОДУКТА

Насырова Регина Талгатовна

ассистент филиала ФГБОУ ВПО «Уфимский государственный нефтяной технический университет»,

РФ, г. Салават

E-mail: bareta@bk.ru

Самков Денис Борисович

студент 3 курса, филиал ФГБОУ ВПО «Уфимский государственный нефтяной технический университет»,

РФ, г. Салават

E-mail: dens9526@mail.ru

Покало Юлия Дмитриевна

студент 3 курса, филиал ФГБОУ ВПО «Уфимский государственный нефтяной технический университет»,

РФ, г. Салават

E-mail: ypokalo@mail.ru

CHOICE OF METHOD ROOTS UPDATE USING THE SOFTWARE

Regina Nasyrova

the assistant to branch “The Ufa state oil technical university”,

Russia, Salavat

Denis Samkov

the student 3 courses, branch “Ufa state oil technical university”,

Russia, Salavat

Yulia Pokalo

the student 3 courses, branch “Ufa state oil technical university”,

Russia, Salavat

АННОТАЦИЯ

Предложен программный продукт для уточнения корней алгебраических уравнений, который выполняет вычисления с высокой точностью четырьмя методами. Результатом работы является программный продукт. Данный программный продукт будет способствовать поиску наиболее эффективного метода решения конкретного уравнения.

ABSTRACT

Proposed software to clarify the roots of algebraic equations, which performs calculations with high accuracy by four methods.The result of a software product. This software will help find the most effective method of solving a particular equation.

Ключевые слова: численный метод; вычислительная математика; корень; точность; отрезок.

Keywords: numerical analysis; computational mathematics; root; precision cut.

В наши дни вычислительная техника (ВТ) представляет собой мощное средство для выполнения вычислений высокой точности. Поэтому появилась возможность отказаться от приближенной трактовки прикладных задач и перейти к их решению в точной постановке. Эффективная эксплуатация современной ВТ немыслима без грамотного применения методов приближенного и численного анализа.

Задача уточнения корней уравнения встречается в различных областях научных исследований и актуальна в наши дни. Она часто является элементарным шагом при решении научных и технических задач.

Численные методы ориентированы на решение задач, возникающие на практике. Решение задач данными методами происходит за счёт применения арифметических и логических действий над числами, что позволяет эффективно применять ВТ. Условия и решения задач чаще всего являются неточными, что является следствием наличия погрешностей. Причиной их присутствия может стать несоответствие построенной математической модели реальному объекту, погрешность исходных данных, погрешность метода решения, погрешность округления и т. д.

Решение алгебраических уравнений представляет собой одну из самых распространённых задач прикладного анализа, необходимость которой возникает в многочисленных и самых разнообразных разделах физики, механики и естествознания при самой разнообразной трактовке данных терминов.

Этап уточнения корней заключается в том, что находится приближенное значение корня, принадлежащего отрезку [a,b], с заданной точностью (погрешностью) ε. Говоря о погрешностях вычислений, следует отметить, что

,

где: x – точное значение корня,

 – приближенное значение корня,

ε – погрешность.

На практике широкое распространение получили следующие методы уточнения корней:

1)  метод половинного деления;

2)  метод хорд;

3)  метод касательных (Ньютона);

4)  метод простой итерации.

Опишем ход работы каждого метода:

·     метод половинного деления: пусть дана функция y=F(x), которая определена и непрерывна на промежутке [a,b], причем F(a)F(b)<0. Необходимо определить корень на заданном отрезке с точностью ε. Для нахождения корня следует делить отрезок [a,b] пополам точкой . Если , то возможны два случая: F(x) имеет противоположные знаки на отрезке [a,c] или F(x) меняет знак на отрезке [c,b]. Дл последующего уточнения корня следует выбрать тот отрезок, на котором функция меняет знак [1]. Если F(x) меняет знак на отрезке [a,c], то b=c; если F(x) меняет знак на отрезке [c,b], то a=c. Новый уменьшенный отрезок снова делим пополам и проводим тот же анализ. Условием окончания счета станет . В результате получаем на определенном шаге точный корень уравнения: . Погрешность метода:.

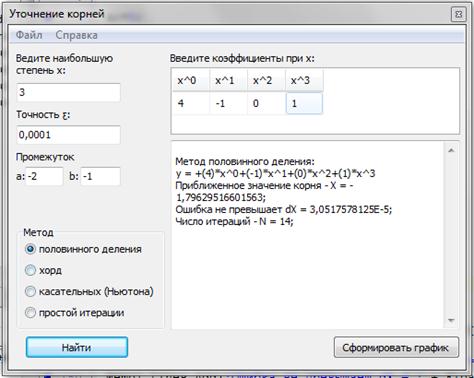
Рисунок 1. Метод половинного деления

·     метод хорд: пусть функция y=F(x) определена и непрерывна на отрезке [a,b] и F(a)F(b)<0. Необходимо найти корень на отрезке с точностью ε. В качестве приближений к корню принимаются значения c₀, c₁, c₂… точек пересечения хорды с осью абсцисс  или . Точка c делит отрезок [a,b] на две части. Ту из них, на которой функция знак не меняет, отбрасываем (аналогично методу половинного деления).

В качестве условия окончания счета можно принять условия:  (Минаева);  (Турчак). Корень уравнения: c_i.

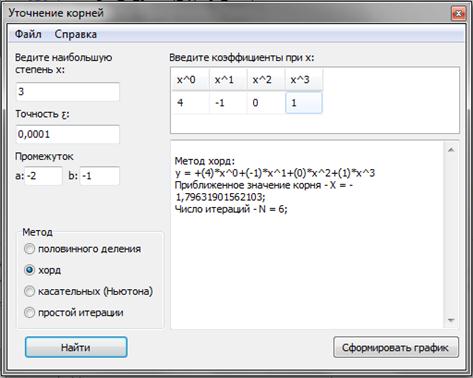
Рисунок 2. Метод хорд

·     метод касательных: пусть функция y=F(x) определена, непрерывна, монотонна и дифференцируема в некоторой окрестности корня. Требуется найти корень на отрезке с точностью ε. На k-ой итерации проводится касательная к графику функции y=F(x) при x=c_k и находится точка пересечения касательной с осью абсцисс [1]. При этом достаточно задать начальное приближение c₀, а не указывать отрезок [a,b].

Уравнение касательной к графику функции y=F(x) в точке x₀ имеет вид: . Пересечение с осью Ox находится из условия y=0, откуда . Таким образом, получается формула для нахождения последовательности c₁, c₂… точек пересечения касательных с осью абсцисс: .Условие окончания счета:. Корень уравнения: c_i+1.

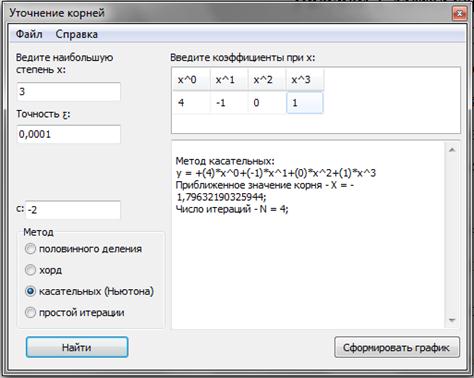
Рисунок 3. Метод касательных

·     метод простой итерации: заменим уравнение F(x)=0 равносильным уравнением x = f(x). Пусть уравнение x=f(x) имеет единственный корень на отрезке [a,b] и выполнены условия:

1) функция f(x) определена и дифференцируема на отрезке [a,b];

2) x[a,b], f(x) [a,b]

3) q,x[a,b], |f’(x)|q<1

Тогда итерационная последовательность x_n=f(x_n-1) (n=1,2,...) сходится при любом начальном члене x₀[a,b]. В зависимости от вида функции сходимость может происходить ступеньками либо по спирали [2].

Для оценки погрешности n-го приближения используется формула . Приняв за нулевое приближение x_n-1 и учитывая, что при 0<q<1 будет qⁿ<q, для оценки погрешности n-го приближения можно использовать формулу .

Значение q можно получить как верхнюю грань модуля производной |f’(x)| при xÎ[a,b]. Чем q меньше, тем быстрее сходится ряд.

Чтобы  достаточно потребовать , откуда получим условие окончания счета .

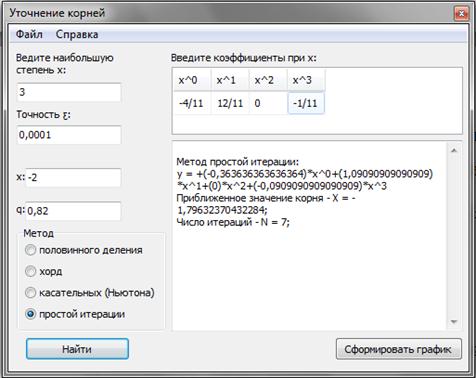
Рисунок 4. Метод простой итерации

Программная реализация решения уравнений, может быть использована как в учебных целях, так и в инженерной сфере. Решение уравнений является одной из задач, наиболее часто встречающихся в практике инженера.

Использование данного программного продуктапозволит выбрать метод решения конкретной задачи в зависимости от предъявляемых требований к скорости и точности.

Список литературы:

1.            Колдаев В.Д. Численные методы и программирование. – М.: ИД «ФОРУМ», 2009. – 336 с.

2.            Умергалин Т.Г. Основы вычислительной математики: Учебное Пособие. – Уфа, Изд-во УГНТУ, 2003. – 106 с.