ОПТИМАЛЬНОЕ  УПРАВЛЕНИЕ  ВИБРАТОРОМ  ДЛЯ  ВНЕДРЕНИЯ  В  ГРУНТ  СВАИ

Ле  Тхи  Тхань

аспирант,  кафедра  математического  моделирования,

Тульский  государственный  университет, 
РФ,  г.  Тула

E-mail: 

OPTIMAL  CONTROL  OF  VIBRATOR  FOR  INTRODUCTION  IN  THE  SOIL  POLING

Le  Thi  Thanh

PhD  student  Department  of  Mathematical  Modeling,

Tula  State  University, 
Russia,  Tula

АННОТАЦИЯ

Задачу  об  оптимальном  управлении  можно  решить  различными  способами.  В  настоящей  работе  минимум  функционала  платы  можно  найти,  построив  функции  состояния  и  функцию  управления  в  виде  многочлена  по  степеням  параметра    с  дополнительным  слагаемым  и  исследовав  на  экстремум  минимизирующий  функционал  по  дополнительному  параметру.

ABSTRACT

The  problem  of  optimal  control  can  be  solved  by  various  methods.  In  this  paper,  the  functional  minimum  fee  can  be  found  by  constructing  functions  of  state  and  function  of  control  in  the  polynomial  form  along  degree  of  parameter    with  additional  summand,  and  research  on  minimizing  functional  extremum  along  additional  parameter.

Ключевые  слова:  оптимальное  управление;  многочлен;  минимум  функционала.

Keywords:  optimal  control;  polynome;  functional  minimum.

Рассмотрим  задачу  о  максимальном  внедрении  в  грунт  сваи,  на  которую  действует  сила,  вырабатываемая  быстрым  управляемым  вибратором  при  минимальных  затратах  энергии  [2].  Математической  моделью  этой  задачи  является  задача  оптимального  управления  материальной  точкой  массы    на  отрезке  времени  .

Динамика  быстрого  управляемого  вибратора  имеет  вид:

,                                     (1)

,                          (2)

где:    –  управление, 

  –  малый  параметр, 

  –  коэффициент  трения,  причем  .  Текущие  расходы

энергии  вибратора    описываются  уравнением

.                                       (3)

Динамика  материальной  точки  имеет  вид

,                                                 (4)

,                                     (5)

где:    –  вертикальная  координата  точки, 

  –  гармоническая  вынуждающая  сила  с  большой  частотой,  создаваемая  вибратором, 

  –  ускорение  свободного  падения, 

  –  сила  трения,  пропорциональная    –  скорости  точки, 

  –  коэффициент  пропорциональности.

Заданы  следующие  условия

,          (6)

.         (7)

Допустимое  управление    принадлежит  классу    измеримых  функций.  Требуется  минимизировать  следующий  функционал  платы:

.

Чтобы  минимизировать  функционал  платы,  нам  надо  найти  функции  состояния  и  функцию  управления  системы,  состоящей  уравнений  (1),  (2),  (3),  (4),  (5)  с  условиями  (6),  (7).

Метод  определения  функции  состояния    и  функцию  управления    в  виде  многочлена  по  степеням  параметра    с  дополнительным  слагаемым  и  метод  проверки  условия  управляемости  мы  знаем.

С  известными  функциями

мы  имеем:

Получим: 

.                 (8)

Выражение  (8)  можно  записать  в  следующем  виде:

  ,

где    неизвестно.

Чтобы  ,  нам  надо  оценить  . 

C  помощью  Mathematica  4.2  мы  получаем:

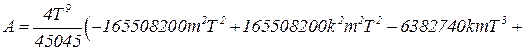
где:    –  малый  параметр, 

  –  коэффициент  трения  (большой),  причем  ,  создаваемая  вибратором, 

  –  коэффициент  пропорциональности, 

  –  большая  масса.  Из  этого  следует,  что  в  последнем  выражении  все  слагаемые,  которые  содержат  ε,  стремятся  к  нулю.

Следовательно, 

Мы  имеем    –  коэффициент  трения  (большой),  причем  ,  создаваемая  вибратором,    –  коэффициент  пропорциональности,    –  большая  масса.  Поэтому:

Действительно,  . 

Имеем    –  квадратный  трехчлен,  где  с  неизвестно,    ,  то  существует  минимум  .  Таким  образом,  существует  такой,  что  ,  где  .

Список  литературы:

1. Андреев  Ю.Н.  Управление  конечномерными  линейными  объектами.  –  М.:  Наука,  1976.  –  424  с. 
2. Колпакова  Е.А.,  Субботина  Н.Н.  Об  определении  асимптотики  одного  класса  сингулярно  возмущенных  задач  вибрационной  механики  //  Автоматика  и  Телемеханика.  –  2007.  –  №  11.  –  C.  150–163.
3. Понтрягин  Л.С.  Обыкновенные  дифференциальные  уравнения.  –  М.:  Наука,  1982.  –  329  с.
4. Уонэм  У.М.  Линейные  многомерные  системы  управления.  –  М.:  Наука,  1980.  –  376  с.