ОБ  ОСНАЩЕНИЯХ  КАРТАНА  БАЗИСНЫХ  ПОДРАССЛОЕНИЙ  СКОМПОНОВАННОГО  SH-РАСПРЕДЕЛЕНИЯ

Будылкин  Андрей  Александрович

аспирант,  институт  прикладной  математики  и  информационных  технологий  Балтийский  федеральный  университет  имени  И.  Канта,

РФ,  г.  Калининград

E-mail: 

ABOUT  CARTAN  EQUIP  OF  BASIS  SUBBUNDLES  OF  COMPOSITED  SH-DISTRIBUTION

Budylkin  Andrey

graduate  student,  Baltic  federal  university  of  I.Kant,  institute  of  applied  mathematics  and  information  technologies

Russia,  Kaliningrad

АННОТАЦИЯ

В  данной  работе  рассмотрим  скомпонованные  распределения  (SH-распределения)  проективного  пространства  [1].  Изучение  SH-распределений  актуально,  так  как  теорию  SH-распределений  можно  применить  для  исследования  регулярных  гиперполос  в  P_n  и  гиперполос  специальных  классов  [6];  [7],  а  также  для  гиперполосных  распределений  [8];  [9].  Для  Λ-,  L-подрасслоений  SH-распределения  построены  оснащения  в  смысле  Э.  Картана  [10].  Найдены  условия  инвариантности  и  неподвижности  плоскостей  Картана  и  связь  оснащения  Картана  с  нормализацией  Нордена  [4].  В  работе  использован  метод  Лаптева  Г.Ф.  [2];  [3]  Индексы  принемают  значения 

ABSTRACT

In  this  paper,  we  consider  the  distribution  of  assembled  (SH-distribution)  projective  space.  Theory  SH-distributions  can  be  applied  to  the  study  of  regular  hyperbands  in  Pn  and  hyperbands  special  classes,  as  well  as  for  hyperband  distributions.  For  Λ-,  L-subbundles  SH-distribution  equipment  constructed  in  terms  of  Cartan.  The  conditions  of  invariance  and  the  stationary  plane  and  communication  equipment  Cartan  Cartan  Norden's  normalization.  The  paper  used  the  method  of  GF  Laptev  ,  The  index  values  Accepted

Ключевые  слова:  распределение;  оснащение;  условия  инвариантности.

Keywords:  distribution;  equipment;  invariance  conditions.

§  1.  О  голономности  SH-  распределения

1.  В  проективном  пространстве  P_n  рассмотрим  скомпонованное  гиперплоскостное  распределение  (SH-распределение)  [1].  Выберем  подвижной  репер  R₀  ={}  нулевого  порядка  ассоциированный  с  SH-распределением 

AA₀,  {A_i}⊂Λ(A₀),  {A_α}⊂L(A₀),  A_nH_n-1(A₀),

формулы  инфинитезимального  перемещения  которого  запишем  в  виде

(1)

Известно  [1],  что  SH-распределение  в  репере  R₀  задается  уравнениями  (2),(3):

         (2)

,  ,

,

,  ,

,                 (3)

,  ,

,

,,

.

Имеет  место  теорема  существования  [1]:

Теорема  1.  В  n-мерном  проективном  пространстве  P_n  скомпонованное  SH-распределение  в  репере  нулевого  порядка  R₀  определено  с  произволом  (2m+1)(n-m-1)  +  m  функций  n  аргументов.

2.  Тензоры  {},{},{},{}  1-го  порядка,  вообще  говоря,  не  симметричны  по  индексам  i,j,  но  именно  ими  охватываются  симметрические  тензоры  },{},{,},{,}:

где 

и  кососимметрические  тензоры  ,{}, {}:

3.  Уравнение 

                                                (4)

Ассоциированное  [2]  с  оснащающим  распределением  гиперплоскостей  Н,  вполне  интегрируемо  тогда  и  только  тогда,  когда  обращается  в  нуль  тензор  {}:

                                                (5)

В  этом  случае  (5)  оснащающее  Н-подрасслоение  определяет  однопараметрическое  семейство  гиперповерхностей  V_n-1,  огибающих  элементы  Н-подрасслоения.  При  смещении  центра  А₀  вдоль  фиксированной  гиперповерхности  V_n-1  уравнения  (2)-(4)  задают  гиперповерхность  V_n-1,  касательные  плоскости  H_n-1  которой  образуют  поле  скомпонованных  плоскостей  таких,  что  в  каждой  точке  А₀nbsp; V_n-1  выполняется  соотношение  [Λ(A₀),L(A₀)]=H_n-1(A₀).  Условия  (5)  характеризуют  голономность  [2]  H-подрасслоения.  Тензор  {}  назовем  тензором  неголономности  оснащающего  Н-подрасслоения.

4.  Аналогично,  система    ассоциированная  с  базисным  распределением  плоскостей  L_n-m-1,  вполне  интегрируема  тогда  и  только  тогда,  когда  обращается  в  нуль  тензор  {,}:

                 (6)

В  этом  случае  (6)  L-подрасслоение  порождает  (m+1)-параметрическое  семейство  поверхностей  V_n-m-1,  огибаемых  плоскостями  L_n-m-1  (элементами  L-подрасслоения).

При  смещении  центра  А₀  вдоль  фиксированной  поверхности  V_n-m-1  уравнения  (2),(3)  вместе  с    представляют  собой  дифференциальные  уравнения  регулярной  (n-m-1)-мерной  гиперполосы  [6];  [7],  оснащенной  полем  Λ-плоскостей.  Такие  гиперполосы  назовем  гиперполосами  H_n-m-1(Λ).  Следовательно,  обращение  в  нуль  тензора  {,}  есть  условие,  при  котором  пространство  P_n  расслаивается  на  (m+1)-параметрическое  семейство  регулярных  гиперполос  H_n-m-1(Λ)  так,  что  каждая  плоскость  L_n-m-1(A₀)  в  центре  А₀  является  касательной  плоскостью  базисной  поверхности  V_n-m-1  гиперполосы  H_n-m-1(Λ).  Тензор  {,}  назовем  тензором  неголономности  [6];  [7]  L-подрасслоения.

5.  Также  система  ,  ассоциированная  с  базисным  распределением  плоскостей  Λ_m,  вполне  интегрируема  тогда  и  только  тогда,  когда  обращается  в  нуль  тензор :

           (7)

В  этом  случае  (7)  базисное  Λ-подрасслоение  определяет  (n-m)-параметрическое  семейство  m-мерных  поверхностей  (плоскости  Λ_m  огибаются  m-мерными  поверхностями  (n-m)-параметрического  семейства).  При  смещении  центра  А₀  вдоль  фиксированной  поверхности  V_m  уравнения  (2),(3)  вместе  с    представляют  собой  дифференциальные  уравнения  регулярной  m-мерной  гиперполосы,  оснащенной  полем  L-плоскостей.  Такие  гиперполосы  назовем  H_m(L).  Следовательно,  обращение  в  нуль  тензора  {,}  есть  условие,  при  котором  пространство  P_n  расслаивается  на  (n-m)-параметрическое  семейство  регулярных  гиперполос  H_m(L)  так,  что  каждая  плоскость  Λ_m(A₀)  в  центре  А₀  является  касательной  плоскостью  базисной  поверхности  V_m  гиперполосы  H_m(L).  Таким  образом,  условия  (7)  определяют  голономность  [2]  Λ-подрасслоения.  Тензор  {,}  назовем  тензором  неголономности  Λ-подрасслоения.

Определение.  Скомпонованное  Н-распределение  назовем  голономным  [9],  если  оба  базисных  подрасслоения  (L  и  Λ)  голономны,  т.е.  выполняются  условия  (6),  (7)  и  полуголономным,  если  выполняется  только  одно  условие:  либо  (6),  либо  (7).

6.  В  общем  случае  плоскость  L(A)  в  каждом  центре  А  не  совпадает  с  характеристикой  Х_n-m-1(A)  [9]  гиперплоскости  Н(А),  т.  е. 

.

В  частности,  если 

,

то  SH(L)  распределение  есть  гиперполосное  распределение,  которое  исследовал  Столяров  А.В.  [9]  Таким  образом,  теорию  регулярного  скомпонованного  SH-распределения  проективного  пространства  P_n  можно  применить  как  для  исследования  регулярных  гиперполос  H_m  ⊂  P_n  и  гиперполос  специальных  классов,  так  и  для  гиперполосных(полосных)  распределений.

§2.  Инвариантное  оснащение  Λ-подрасслоения  данного  SH-распределения  в  смысле  Э.  Картана

1.  В  дифференциальной  окрестности  1-го  порядка  рассмотрим  квазитензоры  {},{},{},{},  компоненты  которых  удовлетворяют  соответственно  уравнениям:

                       (8)

              (9)

      (10)

           (11)

Уравнения  (9),(8)  задают  нормали  1-го  рода  [1],  а  уравнения  (11),(10)  задают  поля  нормалей  2-го  рода  соответственно  L-подраслоения  и  Λ-подрасслоения  в  дифференциальной  окрестности  1-го  порядка.

Охваты  (10),(11)  носят  более  общий  характер:

  (12)

где  квазитензоры  ,  {}  задают  соответственно  нормали  1-го  рода  Λ-  и  L-подрасслоений  произвольного  порядка,  а  квазитензоры  {},  {}  —  задают  нормали  2-го  рода  Λ-  и  L-подрасслоений  того  же  порядка.

Определение.  Λ-подрасслоение  m-  мерных  линейных  элементов  данного  SH-распределения  назовем  оснащенным  в  смысле  Э.  Картана  [10],  если  каждому  центру  А₀  поставлена  в  соответствии  плоскость  K_n-m-1(A₀),  не  имеющая  общих  точек  с  текущим  элементом  Λ_m(A₀)  базисного  Λ-подрасслоения. 

Плоскость  K_n-m-1(A₀)  в  каждом  центре  А₀  зададим  точками

.(11)

Функции,  входящие  в  соотношения  (11),  удовлетворяют  уравнениям

                                    (13)

которые  задают  условие  инвариантности  плоскости  Картана 

K_n-m-1(A₀)  =  [K_α,  K_n].  В  дальнейшем,  если  специально  не  оговорено,  в  качестве  функций    берем  соответственно  охваты 

если    то  .  Таким  образом,  оснащение  Λ-подрасслоения  данного  SH  -  распределения  в  смысле  Э.  Картана  равносильно  заданию  на  подмногообразии  SH  полей  геометрических  объектов  ,{},{}.  Заметим,  что  плоскость  K_n-m-1(A₀)  пересекает  L_n-m-1(A₀)  по  плоскости 

K_n-m-2(A₀)=  L_n-m-1(A₀)  K_n-m-1(A₀)=  [  K_α]=[  K_α=+],

и  если  ,  то  плоскость  K_n-m-2(A₀)  является  осью  плоскости  Кёнигса  [5].  В  силу  этого  плоскость  K_n-m-2(A₀)  =  [K_α]  назовем  осью  оснащающей  плоскости  K_n-m-1(A₀)  =  [K_α,  K_n].  Ясно,  что  оснащение  Λ-подрасслоения  в  смысле  Э.  Картана  влечет  за  собой  оснащение  Λ-подрасслоения  полем  нормалей  1-го  рода .  Верно  и  обратное  утверждение:  если  на  Λ-подрасслоении  задано  поле  нормалей  1-го  рода  ,  то  такое  оснащение  определяет  оснащение  в  смысле  Э.  Картана  Λ-подрасслоения,  так  как  в  качестве  одного  из  возможных  охватов  функции    можно  взять

                       (14)

или 

  .                              (15)

При  таком  охвате  (14),(15)  функции    оснащающая  плоскость  K_n-m-1(А₀)  —  называется  плоскостью  Кёнигса  [10]  нормали  {}.  Охват  (15)  универсален  в  том  смысле,  что  он  справедлив  для  любого  поля  нормалей  1-го  рода  {}.  Из  охвата  (15)  функции    следует:

Теорема  2.  В  каждом  центре  А₀  SH-распределения  инвариантные  оснащающие  плоскости  Кёнигса  ()  всех  нормалей  1-го  рода  N_n-m(  Λ-подрасслоения  принадлежат  одной  связке,  (n-m-2)-мерная  вершина  K_n-m-2=[  которой  является  осью  каждой  из  плоскостей  Кёнигса.

2.  Пусть  Λ-подрасслоение  оснащено  полями  нормалей  {}  1-го  рода.  Следуя  работе  Столярова  А.В.  [8],  найдем  условия  неподвижности  плоскости  Э.  Картана  K_n-m-1(А₀)  =  [K_α,  K_n].  Разложив  dK_α,  dK_n  по  реперу  {A₀,A_j,  K_β  ,  K_n  }  и  приравняв  коэффициенты  при  A₀,  A_j  к  нулю,  находим

  (16)

           (17)

,  (18)

.                               

Одновременное  выполнение  соотношений  (18),(19)  является  условием  того,  что  смещение  оснащающей  плоскости  K_n-m-1()  не  выходит  из  нормали  1-го  рода  N_n-m().  При  этом  оснащающая  плоскость  K_n-m-1()  является  плоскостью  Кёнигса  [3]  нормали  {},  так  как  из  соотношений  (19),(18)  непосредственно  следует 

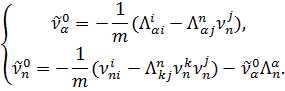
В  работе  [9]  доказано,  что  при  m2  для  гиперполосных  распределений  из  соотношений  (18),(19)  вытекают  соотношения  (16),(17).  Так  же  можно  показать,  что  для  Λ-подрасслоения  данного  SH-распределения  условий  (18),(19)  достаточно,  чтобы  восстановить  (16),(17).  В  случае  m2  аналогично  доказываем,  что  при  любом  смещении  центра  А₀  SH-распределения  смещение  оснащающей  плоскости  Э.  Картана  K_n-m-1  не  выходит  из  нормали  1-го  рода  {}  тогда  и  только  тогда,  когда  оснащающая  плоскость  K_n-m-1  неподвижна.  В  этом  случае  плоскость  K_n-m-1  является  плоскостью  Кёнигса  [9]  нормали  {}.

§  3.  Инвариантное  оснащение  L-подрасслоения  в  смысле  Картана

1.  Пусть  теперь  задано  поле  нормалей  1-го  рода  {}  L-подрасслоения.  Тогда  поле  квазитензора

заданное  уравнениями

определяет  поле  нормалей  2-го  рода  L-подрасслоения.

Определение.  L-подрасслоение  (n-m-1)-мерных  плоскостей  данного  SH-распределения  назовем  оснащенным  в  смысле  Картана  [10],  если  каждому  центру  А₀  поставлена  в  соответствие  плоскость  К_m(A₀),  не  имеющая  общих  точек  с  текущим  элементом  L(A₀)  базисного  L-подрасслоения.

В  плоскости  нормали  N_m+1()  найдем  ивариантную  плоскость  К_m()=[C_i,C_n],  натянутую  на  точки:

,  ,

uде

Согласно  (1),(2),(9),(12),(13)  находим  условия  инвариантности  плоскости  К_m()=[C_i,C_n]:

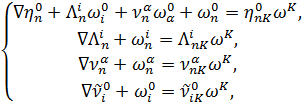                            (20)

Таким  образом,  оснащение  L-подрасслоения  данного  SH-распределения  в  смысле  Э.  Картана  равносильно  заданию  на  подмногоообразии  SH  полей  геометрических  объектов  {},{},{,}  (20).  Отметим  что  плоскость  K_m()  пересекает  плоскость  Λ_m(A₀)  по  плоскости 

K_m-1(A₀):K_m-1(A₀):  K_m(A₀)    Λ_m(A₀)  =  [,

которую  будем  будем  называть  осью  плоскости  K_m  Э.  Картана.  Ясно,  что  если  ,  то  плоскость  K_m-1(A₀)  является  осью  плоскостей  Кёнигса  [3]  в  этом  случае 

,  .

Оснащение  L-подрасслоения  в  смысле  Э.  Картана  полем  плоскостей  K_m()  влечет  за  собой  оснащение  L-подрасслоения  полем  нормалей  1-го  рода  {}.  Верно  и  обратное  утверждение:  если  на  L-подрасслоении  задано  поле  нормалей  1-го  рода  {},  то  такое  оснащение  определяет  оснащение  в  смысле  Э.  Картана  L-подрасслоения,  так  как  в  качестве  одного  из  возможных  охватов  функции    можно  взять

                          (21)

или

.                         (22)

При  охвате  (21),(22)  функции   оснащающая  плоскость  K_m(A₀)  [9]  является  плоскостью  Кёнигса  нормали  {}.  Охват  (22)  универсален  в  том  смысле,  что  он  справедлив  для  любого  поля  нормалей  {}  1-го  рода  L-подрасслоения  в  данном  центре  А₀.

2.  Пусть  L-подрасслоение  оснащено  полем  нормалей  {}  1-го  рода.  Аналогично  (см  §2)  найдем  условия  неподвижности  плоскости  Э.Картана  К_m(A₀)=[C_i,C_n].  Разложив  dC_n,  dC_i  по  реперу  {A₀,A_α,C_i,C_n}  и  приравняв  коэффициенты  при  A₀  и  A_α  к  нулю,  находим

(23)

(24)

    (25)

.                                         (26)

Следуя  работе  [8]  можно  показать,  что  условия  (23),(24)  являются  следствиями  (25),  (26),  а  при  n-m-12  условий  (25),(26)  достаточно,  чтобы  плоскость  Э.  Картана  К_m(A₀)  была  неподвижной.  В  этом  случае  плоскость  К_m(A₀)  является  плоскостью  Кёнигса  [9]  так  как  из  (25),  (26)  следует,  что

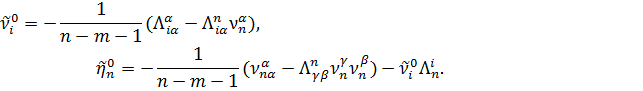
Для  инвариантных  оснащений  в  смысле  Картана  L-подрасслоения  имеет  место  теорема  аналогичная  теореме  2.

Теорема  3.  В  каждом  центре  А₀  SH-распределения  инвариантные  оснащающие  плоскости  Кёнигса  ()  всех  нормалей  1-го  рода  N_m+1()  L-  подрасслоения  принадлежат  одной  связке,  (m-1)-мерная  вершина  K_m-1=[  которой  является  осью  каждой  из  плоскостей  Кёнигса  K_m(A₀).

Резюмируя,  приходим  к  следующим  предложениям

Теорема  4.  При  m2  при  любом  смещении  центра  А₀  SH-распределения  в  дифференциальной  окрестности  1-го  порядка  оснащающая  плоскость  Э.  Картана  K_n-m-1=[K_α(),  K_n()]  (является  плоскостью  Кёнигса)  не  выходит  из  нормали  1-го  рода  {}  Λ-подрасслоения  тогда  и  только  тогда,  когда  она  неподвижна.  Условия  (18),(19)  —  аналитический  признак  неподвижности  плоскости  Кёнигса  K_n-m-1. 

Теорема  5.  При  n-m-12  при  любом  смещении  центра  А₀  SH-распределения  в  дифференциальной  окрестности  1-го  порядка  оснащающая  плоскость  Э.  Картана  К_m()=[C_i,C_n]  (плоскость  Кёнигса)  не  выходит  из  нормали  1-го  рода  {}  L-подрасслоения  тогда  и  только  тогда,  когда  она  неподвижна.  Условия  (22),(23)  —  аналитический  признак  того,  что  «вращаясь»  вокруг  своей  оси  K_n-m-2  =[],  плоскость  К_m  остается  неподвижной. 

Список  литературы:

1. Будылкин  А.А.  Инвариантные  нормализации  скомпонованного  гиперплоскостного  распределения  проективного  пространства//  Естественные  и  математические  науки  в  современном  мире/  г.  Новосибирск,  —  2015.  —  вып.  №  2(26)  —  с.  24—33.
2. Лаптев  Г.Ф.  Распределение  касательных  элементов.  Тр.  Геометр.  семинара.  ВИНИТИ,  АНСССР,  —  1971.  —  т.  3,  —  с.  29—48.
3. Лаптев  Г.Ф.,  Остиану  Н.М.  Распределения  m-мерных  линейных  элементов  в  пространстве  проективной  связности.  Труды  геометрического  семинара.  Т.  3.  —  М-ВИНИТИ  АН  СССР,  1971,  —  с.  49—94.
4. Норден  А.П.  Пространства  аффинной  связности.  М.  изд.  «Наука»,  1976.  —  432  с.
5. Остиану  Н.М.  Распределение  гиперплоскостных  элементов  в  проективном  пространстве.  Тр.  Геометрич  семинара.  АНСССР,  —  1973.  —  т.  4  —  с.  71—120.
6. Попов  Ю.И.  Общая  теория  регулярных  гиперполос:  учебное  пособие  /Калининград  ун-т,  Калининград,  1988,  —  82  с.
7. Попов  Ю.И.  Столяров  А.В.  Специальные  классы  гиперполос  проективного  пространства.  Учебное  пособие,  Калининград,  БФУ  им.  И.  Канта,  —  122  с.
8. Столяров  А.В.  Двойственная  теория  оснащенных  многообразий;  Монография  2-е  изд.  /  Чуваш.  Ин-т,  Чебоксары  1994  г.  —  290  с.
9. Столяров  А.В.  Проективно-дифференциальная  геометрия  регулярного  гиперполосного  распределения  m-мерных  линейных  элементов  //  Проблемы  геометрии//  ВИНИТИ  АНСССР  —  1975.  —  Т.  7.  —  с.  117—151.
10. Cartan  E.  Les  espaces  a  connexion  projective  //  Тр.  семинара  по  векторному  и  тензорному  анализу  /  МГУ.  М.  —  1977.  —  вып.  4  —  с.  147—159.