ГИПЕРПОЛОСНОЕ  РАСПРЕДЕЛЕНИЕ  H(L)  АФИННОГО  ПРОСТРАНСТВА

Попов  Юрий  Иванович

канд.  ф-м.  наук,  профессор  института  прикладной  математики  и  информационных  технологий 
Балтийский  федеральный  университет  имени  И.  Канта, 

РФ,  г.  Калининград

E-mail: 

 

HYPERBAND  DISTRIBUTION  H(L)  OF  AFINNE  SPACE

Yuri  Popov

candidate  of  science,  professor  of  institute  of  applied  mathematics  and  information  technologies 
Baltic  federal  university  of  I.  Kant,

Russia,  Kaliningrad

 

АННОТАЦИЯ

Дано  задание  H(L)-распределения  [7];  [8]  в  репере  0-го  порядка  и  репере  1-го  порядка.  Введено  соответствие  Бомпьяни-Пантази  между  нормалями  1-го  и  2-го  рода  основных  структурных  подрасслоений  данного  H(L)-распределения.  Для  H-,X-,L-подрасслоений  найдены  их  фокальные  многообразия,  а  также  поля  нормализаций  и  пучки  нормалей  1-го  и  2-го  рода  Нордена  в  дифференциальной  окрестности  1-го  порядка.  Изучение  H(L)-распределений  актуально,  так  как  теорию  H(L)-распределений  можно  применить  для  изучения  торсовых  поверхностей,  регулярных  одномерных  гиперполос,  а  также  специальных  классов  гиперполос  и  гиперповерхностей  афинного  пространства.  Работа  выполнена  методом  Лаптева  Г.Ф.  [3].  В  работе  индексы  принимают  значения:

 

 

ABSTRACT

Given  the  task  of  H(L)-distribution  in  the  frame  of  zero  order  and  datum  of  the  1st  order.  Permission  ratio  Bompiani  -  Pantazi  between  the  normals  of  the  1st  and  2nd  kind  of  major  structural  subbundles  of  H(L)-Distribution  (H-,  X-,  L-  subbundles).  For  H-,  X-,  L-subbundles  found  their  focal  manifolds,  as  well  as  the  field  of  normalization  and  the  normal  bundles  of  1st  and  2nd  kind  Nord  differential  neighborhood  of  the  1st  order.  Study  of  H  (L)-distributions  of  actual,  as  the  theory  of  H  (L)-distributions  can  be  used  to  study  torsovyh  surfaces,  dimensional  hyperbands  regular  and  special  classes  hyperbands  and  hypersurfaces  of  affine  space.  This  work  by  GF  Laptev.  In  all  the  indices  take  the  values:

 

 

Ключевые  слова:  гиперполосное  распределение;  афинное  пространство;  фокальный  образ.

Keywords:  hyperband  distribution;  affine  space;  focal  image.

 

§  1.  Задание  гиперполосного  H(L)-распределения  аффинного  пространства

1.  Пусть  дано  n-мерное  аффинное  пространство  A_n,  отнесенное  к  подвижному  реперу  {А,},  дифференциальные  уравнения  инфинитезимального  перемещения  которого  имеет  вид

 

         (*)

 

Инвариантные  формы    и    аффинной  группы  преобразований  удовлетворяют  структурными  уравнениями  аффинного  пространства  A_n:

 

 

Рассмотрим  H(L)-распределение  аффинного  пространства  А_n.  При  этом  распределение  прямых  L(A)  назовем  базисным  распределением  (или  L-подрасслоением),  а  распределение  гиперплоскостей  H(A)-оснащающим  распределением  (или  H-подрасслоением).  В  репере  R⁰ 

(})  H(L)-распределение  задается  уравнениями:

 

  (1)

 

В  дальнейшем  мы  рассматриваем  регулярные  гиперполосные  распределения  [7];  [8]  для  которых  главный  фундаментальный  тензор    что  позволяет  ввести  в  рассмотрение  обратный  фундаментальный  тензор  1-го  порядка 

 

                                 (2)

 

Из  уравнений  (1)  следует,  что  регулярное  H(L)-распределение  аффинного  пространства  A_n  существует  и  определяется  с  произволом  2(n-2)+1=2n-3  функций  n  аргументов  в  дифференциальной  окрестности  1-го  порядка.

2.  Для  регулярного  Н-распределения  согласно  лемме  Н.М.  Остиану  [6]  возможна  частичная  канонизация  репера  R⁰,  как  это  следует  из  дифференциальных  уравнений

 

                            (3)

 

Действительно,  полагая 

 

 

и  учитывая  (2),  разрешим  уравнения  (3)  относительно  форм 

 

.

 

Геометрический  смысл  такой  канонизации  заключается  в  том,  что  векторы  {}  помещаются  в  характеристику  X_n-m-1(A)  гиперплоскости  H(A),полученную  при  смещении  центра  А  вдоль  кривых,  принадлежащих  L-подрасслоению.  Выбранный  таким  образом  репер  R₁  [6]  является  репером  1-го  порядка  H(L)-распределения.  В  дифференциальной  окрестности  2-го  порядка  H(L)-распределение  задается  относительно  репера  R  [6]  уравнениями:

 

    (4)

                 (5)

 

где  коэффициенты  в  правых  частях  уравнений  (5)  не  симметричны  по  нижним  индексам.  Отметим,  что  геометрические  объекты  Г₁={},  Г₂={Г₁,}  являются  фундаментальными  геометрическими  объектами  H(L)-распределения  соответственно  1-го  и  2-го  порядка  [3].  В  общем  случае  (при  локальной  постановке  вопроса)  определители    отличны  от  нуля.  Компоненты  определителя  Н₀  имеют  следующее  строение

 

 

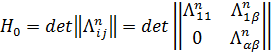
и  удовлетворяют  дифференциальным  уравнениям 

 

.

 

Для  невырожденных  тензоров  {}  и  {}  введем,  вообще  говоря,  несимметрические  обращенные  тензоры  1-го  порядка  {}  и  {},  компоненты  которых  удовлетворяют  соотношениям  [3];  [4]:

 

 

и  соответственно  дифференциальным  уравнениям

 

 

Тензоры  {},  {}  и  {},  {}  являются  фундаментальными  тензорами  1-го  порядка  и  обращенными  фундаментальными  тензорами  1-го  порядка  соответственно  Х-подрасслоения  (распределение  характеристик  Н(L)-распределения)  и  Н-подрасслоения  (распределения  Н-плоскостей)

 

§  2.  Соответствие  Бомпьяни-Пантази

1.  Следуя  работам  [1];  [4]  введем  биекцию  Бомпьяни-Пантази  между  нормалями  1-го  и  2-го  рода,  для  H-,  L-,  X-подрасслоений,  ассоциированных  с  H(L)-распределением.

Определение.  Нормалью  1-го  рода  элемента  Н-распределения  (плоскости  Н(А))  называется  инвариантная  прямая  N₁(A),  удовлетворяющая  условию  N₁(A)H(A)=A,  а  нормалью  2-го  рода  —  инвариантная  плоскость  _n-2(A)  такая  что,  _n-2(A)⊂Н(А),  А∉_n-2(A).

Поля  нормалей  1-го  рода  N₁(A)  и  нормалей  2-го  рода  _n-2(A)  задаются  соответственно  полями  объектов  {},{}:

 

 

Определение.  Будем  говорить,  что  Н-подрасслоение  (соответственно  L-подрасслоение,  Х-подрасслоение)  нормализовано,  если  оно  одновременно  оснащено  полями  нормалей  1-го  рода  и  2-го  рода  Нордена  [5],  а  саму  нормализацию  будем  обозначать    или  (N₁,_n-2)  (соответственно  символами    или  (N_n-1,₀),  (N₂,_n-3)).

2.  Зададим  точку  FH(A)  следующим  образом

 

,                                            (6)

 

Потребуем,  чтобы  она  не  выходила  из  гиперплоскости  Н(А)  при  смещении  центра  А  Н(L)-распределения  вдоль  кривой 

 

,

 

касающейся  нормали  =[A,]  =  [А,]  1-го  рода  гиперплоскости  Н(А),  т.  е.,  чтобы 

 

,  ().                                 (7)

 

Определение.  Точка  F,  удовлетворяющая  условию  (7)  называется  фокальной  точкой  гиперплоскости  Н(А)  [1];  [6]  а  направление  смещения  точки  А,  соответствующие  фокальной  точке  F-фокальным  направлением.

Из  (7)  в  силу  (*),  (6)  следует

 

                          (8)

 

Уравнение  (8)  определяет  многообразие  фокальных  точек  гиперплоскости  Н(А),  которые  согласно  (3),(4),(5)  приведем  к  виду:

 

                               (9)

 

где 

 

          (10)

.

 

Таким  образом,  уравнения  (9)  задают  в  локальном  репере  R₁  [1]  нормаль  2-го  рода  плоскости  Н(А),  а  поле  нормалей  2-го  рода  Н-подрасслоения  задается  дифференциальными  уравнениями  (10).  Разрешим  уравнения  (10а)  относительно 

 

         (11)

 

где

 

                  (12)

 

Итак,  при  помощи  формул  (10а)  и  (11а)  устанавливается  взаимно  однозначное  соответствие  между  нормалями  1-го  и  2-го  рода  Н-распределения.  Это  соответствие  (биекция)  является  для  оснащающего  Н-подрасслоения  аналогом  соответствия  Бомпьни-Пантази  [1];  [4].

Аналогично,  устанавливаем  соответствие  Бомпьяни-Пантази  между  нормалями  1-го  рода  N₂()  и  нормалями  2-го  рода  _n-3()  Х-подрасслоения:

 

           (13)

                        (14)

 

где 

 

                 (15)

 

3.  Из  (12)  следует,  что  компонента  {}  квазитензора  {}  имеет  следующее  строение

 

 

и  является  квазитензором  1-го  порядка

 

.                                             (16)

 

Будем  искать  соответствие  Бомпьяни-Пантази  между  нормалями  1-го  и  2-го  рода  L-подрасслоения  в  виде  (11),  (13)

 

                       (17)

 

Разрешив  уравнения  (17)  относительно  величины  {}  получим

 

,

 

где

 

 

4.  Отметим,  что  поле  квазитензора  {}  (12)  для  гиперплоскостного  распределения  аффинного  пространства  было  введено  Алшибая  Э.Д.  [1];  [2]  и  дана  его  геометрическая  интерпретация.  В  силу  этого  поле  нормалей  1-го  рода  N_{1  1}  (поле  нормалей  )  оснащающего  Н-подрасслоения  данного  Н(L)-распределения,  будем  называть  в  дальнейшем  полем  нормалей  Алшибая  Э.Д.  В  соответствии  с  этой  терминологией  поле  нормалей  1-го  рода  N₂₂  (N_n-1n-1),  определяемое  полем  квазитензора    (15)  (),  назовем  полем  нормалей  Алшибая  1-го  рода  Х-подрасслоения  (L-подрасслоения).  Следуя  работам  [1];  [2]  аналогично  можно  показать,  что  свойства  нормалей  Алшибая    сохраняют  силу  и  в  случае  H(L)-распределения:

а.   при  смещении  центра  А  H(L)-распределения  вдоль  кривой,  касающейся  нормали  Алшибая  ,  гиперплоскостной  элемент  Н(А)  смещается  параллельно;

б.  в  биекции  Бомпьяни-Пантази  (11)  нормали  Алшибая  ,  определенной  объектом  {}  (12),  соответствует  бесконечно  удаленная  (n-2)  —  плоскость  гиперплоскости  Н(А)  (в  этом  случае  в  уравнении  (10)  ).

 

§  3.  Фокальные  образы

1.  Пусть  задано  поле  нормалей  1-го  рода  N₁=[A,]  оснащающего  Н-подрасслоения:

 

.

 

Рассмотрим  фокальные  образы,  связанные  с  L-,  X-подрасслоениями  данного  H(L)-распределения.  Найдем  фокальное  многообразие    нормали  1-го  рода  N_n-1(A)=[A,]  прямой  L(A)  при  смещении  центра  А  вдоль  кривых  (),  принадлежащих  L-подрасслоению:

 

 

Пусть  F  —  фокальная  точка  плоскости  N_n-1(A):

 

 

где

 

 

Из  условия  ее  фокальности

 

 

в  силу  соотношений  (1),  (3),  (14),  (17)  находим 

 

  (18)

 

где 

 

 

Так  как  уравнения  (18)  выполняются  тождественно,  то

 

 

где 

 

         (19)

 

Итак,  фокальное  многообразие  Ф(N_n-2,L),  которое  в  локальном  репере  R¹  задается  уравнениями

 

 

есть  плоскость  K_n-2⊂N_n-1(A).  Плоскость  K_n-2­(А)  является  аналогом  плоскости  Кёнигса  [8]  для  данного  H(L)-распределения.  Точку  пересечения  нормали    с  плоскостью  K_n-2­(А),  т.  е.  точку

 

,

 

назовем  точкой  Кёнигса  нормали  ,  ассоциированной  с  L-подрасслоением  или  кратко    —  виртуальной  точкой  Кенигса.  Определим  в  каждом  центре  А  еще  одну  инвариантную  плоскость 

 

К_n-3(A)=X(A)  K_n-2­(А):  (20)

 

которая  является  нормалью  2-го  рода  плоскости  X(A).  Итак,  структура  плоскости  Кенигса    такова,  что 

 

.

 

Если  задать  другое  поле  инвариантных  нормалей    H-подрасслоения,  то  в  соответствующей  точке  А  плоскость  Кенигса  имеет  вид

 

,

 

т.  е.  плоскость    есть  ось  оснащающих  плоскостей  Кёнигса  в  нормалях  1-го  рода  N_n-1  L-подрасслоения  в  данном  центре  А.

Следовательно,  имеет  место

Теорема  1.  Для  пучка  нормалей  1-го  рода  N_n-1(A)  прямой  L(А)  в  данном  центре  А  все  плоскости  Кенигса  проходят  через  неподвижную  (инвариантную)  плоскость    (20)  —  ось  пучка  плоскостей  Кенигса.

2.  Аналогично,  находим  в  каждом  центре  А  фокальное  многообразие  Ф(N₂,X(A))  нормали  1-го  рода  N₂(А)  плоскости  X(A),  при  смещениях  центра  А  вдоль  кривых  ():

 

 

принадлежащих  Х-подрасслоению.

Зададим  фокальную  точку  F  плоскости  N₂(A)  вектором:

 

 

где

 

 

Требование  инвариантности  точки  F,  т.  е.

 

 

приводит  к  соотношениям

 

            (21)

 

где 

 

                              (22)

 

Условие  (21)  выполняется  тождественно,  поэтому

 

           (23)

 

Свертывая  по  α  и  β  выражение  (23)  и  преобразуя,  получим

 

 

где 

 

                               (24)

             (25)

 

Таким  образом,  фокальное  многообразие  Ф(N₂,Х),  представляет  собой  прямую  ⊂N₂(A),  которая  относительно  локального  репера  R¹  задается  системой  уравнений:

 

                                (26)

 

Прямую    (26)  назовем    —  виртуальной  прямой  Кёнигса  плоскости  N₂(A)  =  [A,L,]  в  центре  А.

Поле  прямых  (26)  задается  уравнениями  (24),(25),(14)  т.  е.  полями  объектов  {},{,}.

Точка    =    является  нормалью  2-го  рода  в  смысле  Нордена  прямой  L(A):

 

                   (27)

 

Если  тензор  ,  то  точка  ⊂L(A)  есть  несобственная  точка  прямой  L(A).  Точку    (27)  назовем    —  виртуальной  точкой  Кёнигса  прямой  L(A),  так  как  она  зависит  от  выбора  нормали  {}  (нормали  плоскости  H(A)).

Точку

 

,

 

·     точку  пересечения  нормали  N₁()  c  прямой    (26),  назовем  точкой  Кёнигса  нормали  N₁=[A,],  ассоциированной  с  плоскостью  X(A),  или  коротко  X  —  виртуальной  точкой  Кёнигса.  Итак,  структура  прямой  (26)  такова:

 

=[,].

 

Заметим,  что  порядок  охвата  тензоров    (19),    (25),  на  единицу  выше,  чем  порядок  объекта  {}(14).

 

§  4.  Поля  нормализаций  и  пучки  нормалей  1-го  и  2-го  Нордена  основных  структурных  подрасслоений  H(L)-распределения  в  дифференциальной  окрестности  1-го  порядка

1.  Согласно  уравнениям  (5),  (2)  убеждаемся,  что  функции 

 

,                      (28).

 

образуют  квазитензор  1-го  порядка  и,  следовательно,  дифференциальные  уравнения  (28)  задают  поле  нормалей  1-го  рода  V₂  X-подрасслоения.

Используя  биекцию  (13),  находим  соответствующее  поле  нормалей  2-го  рода  Х-подрасслоения:

 

 

Далее  с  помощью  объекта  {}  и  соотношения  (22)  построим  тензоры  {}  и  {}:

 

  .  (29)

 

Полю  нормалей  2-го  рода  {}  (29)  в  силу  биекции  (17)  соответствует  поле  нормалей  1-го  рода  {}  L-подрасслоения:

 

, 

 

В  дифференциальной  окрестности  1-го  порядка  введем  функции

 

{},                            (30)

 

удовлетворяющие  соответственно  уравнениям: 

 

.

 

Заметим,  что  геометрические  объекты  (30)  соответствуют  друг  другу  в  биекции  Бомпьяни-Пантази  (10)(или  (11)).

2.  Для  Н-подрасслоения  гиперполосного  Н(L)-распределения  справедливо  предложение,  доказанное  для  гиперплоскостного  распределения  аффинного  пространства  А_n  Алшибая  Э.Д.  [1]/

Теорема  2.  Однопараметрическому  пучку  нормалей  1-го  рода  (();),  определенному  в  данном  центре  А  Н-подрасслоения  (-параметр),  в  биекции  Бомпьяни-Пантази  соответствует  однопараметрический  пучок  параллельных  (n-2)-плоскостей  (пучок  нормалей  2-го  рода),  лежащих  в  плоскости  H(A).

Покажем,  что  аналогичное  предложение  имеет  место  и  для  Х-подрасслоения  данного  H(L)-распределения  пространства  A_n.  Пусть  в  центре  А  H(L)-распределения  задан  пучок  нормалей  1-го  рода  {}  X-подрасслоения  в  смысле  Нордена:

 

,                                  (31)

 

где  объект  {}  задает  произвольную  инвариантную  нормаль  N₂(A)  плоскости  Х(А).  В  силу  формул  (13)  пучку  (31)  в  биекции  (13)  соответствует  пучок  нормалей  2-го  рода,  в  смысле  Нордена  следующего  вида:

 

 

т.  е.  пучок  параллельных  (n-3)-плоскостей,  лежащих  в  плоскости  X_n-2(A). 

Итак,  справедлива

Теорема  3.  Однопараметрическому  пучку  нормалей  1-го  рода  (31)  Х-подрасслоения  в  биекции  Бомпьяни-Пантази  (13)  соответствует  однопараметрический  пучок  параллельных  (n-3)-плоскостей-нормалей  2-го  рода  Нордена  Х-подрасслоения.

Аналогичное  утверждение  имеет  место  и  для  L-подрасслоения.

Теорема  4.  Однопараметрическому  пучку  ()  (32)  нормалей  1-го  рода  Нордена  L-подрасслоения,  где 

 

  ,                                 (32)

 

в  биекции  Бомпьяни  –  Пантази  соответствует  однопараметрическое  семейство  точек  ,  —  нормалей  2-го  рода  в  смысле  Нордена  L-подрасслоения.

3.  Квазитензоры  {},{}  в  общем  случае  функционально  независимы  и  поэтому  определяют  в  дифференциальной  окрестности  1-го  порядка  в  каждом  центре  А  однопараметрический  пучок  нормалей  1-го  рода  Н-подрасслоения: 

 

,                                    (33)

 

которым  в  биекции  (10)  согласно  теореме  3  соответствует  пучок  параллельных  (n-2)-плоскостей  (нормалей  2-го  рода  Н-подрасслоения) 

 

,                                                  (34)

 

где 

 

, 

 

Пучки  (33)  и  (34)  порождают  соответственно  пучки  нормалей  1-го  и  2-го  рода  Х-,  L-подрасслоений  в  смысле  Нордена:

 

, 

, 

 

где 

 

,  ,

,  .

 

В  результате  имеет  место 

Теорема  5.  H(L)-распределение  внутренним  инвариантным  образом  порождает  пучки  нормалей  1-го  рода  (;),  (;),  (;)  и  2-го  рода  (),  (;),  (;)  в  смысле  Нордена  соответственно  H-,X-,  L-  подрасслоений,  а  также  их  нормализации  (;),(;),(;)  в  дифференциальной  окрестности  1-го  порядка.

 

Список  литературы:

1. Алшибая  Э.Д.  Геометрия  распределений  гиперплоскостных  элементов  в  аффинном  пространстве.  Из-во  Тбилисского  ун-та,  Тбилиси,  1999.  —  106  с.
2. Алшибая  Э.Д.  К  геометрии  распределений  гиперплоскостных  элементов  в  аффинном  пространстве  //  Тр.  геометрического  семинара  /ВИНИТИ  АН  СССР.  —  1974.  —  Т.  5.  —  С.  169—193.
3. Лаптев  Г.Ф.  Дифференциальная  геометрия  погруженных  многообразий.  Теоретико-групповой  метод  дифференциально-геометрических  исследований  //  Тр.  Моск.  Об-ва.  —  1953.  —  Т.  2.  —  с.  275—382.
4. Лаптев  Г.Ф.  Остиану  Н.М.  Распределения  m-мерных  линейных  элементов  в  пространстве  проективной  связности  I.//Труды  геометрического  семинара  —  1971.  —  Т.  3  —  с.  49—94.
5. Норден  А.П.  Пространства  аффинной  связности.  М.  1976.  —  432  с.
6. Остиану  Н.М.  О  канонизации  подвижного  репера  погруженного  многообразия//Rev.  Math.  Pures  et  appl(RPR)  —  1962.  —  Т.  7.  —  №  2.  —  С.  239—263.
7. Попов  Ю.И.  Нормали  гиперполосного  распределения  аффинного  пространства//Сб.  «Дифф.  геом.  многообразий  фигур».  —  1988  —  Вып.  19  —  с.  69—79.
8. Столяров  А.В.  Проективно-дифференциальная  геометрия  регулярного  распределения  m-мерных  линейных  элементов//Проблемы  геометрии/Итоги  науки  и  техники  ВИНИТИ  АН  СССР.  —  1975.  —  Т.  7.  —  С.  117—151.