МОДЕЛИ  ПРЫЖКОВОГО  ТРАНСПОРТА  НОСИТЕЛЕЙ  ЗАРЯДА  КАК  ЕДИНАЯ  ОСНОВА  ДЛЯ  АНАЛИЗА  ПОЛЯРИЗАЦИИ  И  ЭЛЕКТРОПРОВОДНОСТИ  В  НЕУПОРЯДОЧЕННЫХ  ДИЭЛЕКТРИКАХ

Ханин  Самуил  Давидович

д-р  физ.-мат.  наук,  профессор,  заведующий  кафедрой  физической  электроники 
Российского  государственного  педагогического  университета  им.  А.И.  Герцена, 
РФ,  г.  Санкт-Петербург

Рябоконь  Дарья  Владимировна

старший  преподаватель  кафедры  физики 
Военной  академии  связи  им.  Маршала  Советского  Союза  С.М.  Буденного, 
РФ,  г.  Санкт-Петербург

Е-mail :  ryabokon90@gmail.com

THE  MODELS  OF  HOPPING  TRANSPORT  OF  CHARGE  CARRIERS  AS  THE  UNIFORM  BASIS  FOR  THE  ANALYSIS  OF  THE  POLARIZATION  AND  CONDUCTIVITY  IN  THE  DISORDERED  DIELECTRICS

Samuil  Khanin

doctor  of  physical  and  mathematical  sciences,  professor,  the  head  of  the  physical  electronics  department 
of  the  Russian  state  pedagogical  university  named  by  A.I.  Herzen, 
Russia,  St.  Petersburg

Darya  Ryabokon

senior  teacher  of  the  physics  department 
of  Military  academy  of  communication  named  by  Marshall  of  the  Soviet  Union  S.M.  Budenny , 
Russia,  St.  Petersburg

АННОТАЦИЯ

Рассматриваются  возможности  совместного  анализа  поляризации  и  электропроводности  в  неупорядоченных  диэлектриках  на  основе  моделей  нестационарной  и  нелинейной  прыжковой  электропроводности.  Развитые  представления  конкретизируются  применительно  к  явлениям  переноса  в  аморфных  диэлектрических  пленках  оксида  тантала.

ABSTRACT

The  possibilities  of  the  conjoint  analysis  of  the  polarization  and  conductivity  in  the  disordered  dielectrics  on  the  basis  of  the  non-stationary  and  nonlinear  hopping  conductivity  models  are  considered.  The  developed  representations  are  concretized  in  relation  to  the  transfer  phenomena  in  tantalum  oxide  amorphous  dielectric  films.

Ключевые  слова:   неупорядоченный  диэлектрик;  прыжковый  транспорт;  релаксационные  токи;  неомическая  проводимость. 

Keywords :  disordered  dielectric;  hopping  transport;  relaxation  currents;  nonohmic  conductivity.

В  ряду  явлений  переноса  заряда,  изучаемых  в  неупорядоченных  диэлектриках,  центральное  место  занимают  поляризация  и  электропроводность.  Это  обусловлено,  по  крайней  мере,  следующими  двумя  обстоятельствами.  Во-первых,  определяющей  ролью  указанных  явлений  в  формировании  функциональных  свойств  электронных  устройств  на  основе  неупорядоченных  диэлектриков.  Во-вторых,  структурной  чувствительностью  этих  явлений,  что  позволяет  восстанавливать  значимые  данные  об  атомном  и  электронном  строении  изучаемых  материалов  на  основе  экспериментально  установленных  закономерностей  электрических  явлений. 

Как  правило,  постановка  задачи  и  исследования  поляризации  и  электропроводности  диэлектриков  осуществляются  сепаратно.  Вместе  с  тем,  для  ряда  диэлектрических  материалов  может  иметь  место  общность  элементарных  актов  поляризации  и  электропроводности,  что  позволяет  осуществлять  их  анализ  с  единых  позиций.  В  настоящей  работе  показывается,  что  основой  для  такого  анализа  могут  служить  модели  нестационарной  и  нелинейной  прыжковой  электропроводности  в  неупорядоченных  системах  [2],  а  результатом  анализа  —  определение  значимых  для  прыжкового  переноса  микроскопических  параметров. 

В  качестве  объекта  исследования  в  работе  выступают  аморфные  диэлектрические  пленки  оксидов  ниобия  и  тантала,  полученные  методом  электрохимического  оксидирования  металлов.  Как  показывает  эксперимент,  для  таких  оксидов  характерна  длительная  изотермическая  релаксация  тока,  предшествующая  установлению  статической  (строго  говоря,  квазистатической)  проводимости  диэлектрика  (рис.  1). 

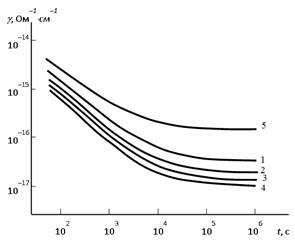
Рисунок  1.  Зависимость  электронной  проводимости  оксида  тантала  от  длительности  нагружения  при  напряжении  электрического  поля  2×10⁵  В/см  (1);  6×10⁵  В/см  (2);  9×10⁵  В/см  (3);  1,5×10⁶  В/см  (4);  3×10⁶  В/см  (5)

Наблюдаемая  степенная  зависимость  релаксационного  тока  от  времени  может  быть  описана  в  рамках  модели  нестационарной  прыжковой  электропроводности,  связывающей  спад  тока  с  увеличением  размера  кластера  локализованных  состояний,  по  которым  происходит  прыжковы   й  транспорт,  с  последовательным  включением  в  него  перескоков  со  всё  меньшей  вероятностью.  Установление  стационарной  проводимости,  по  которой,  как  правило,  судят  об  электропроводности,  происходит,  согласно  данной  модели,  при  включении  наиболее  трудного,  так  называемого,  критического  прыжка,  осуществляемого  с  минимальной  вероятностью  . 

Как  видно  из  рисунка  1,  росту  тока  с  увеличением  напряженности  электрического  поля  предшествует  область  его  падения.  Это  объясняется  в  рамках  рассматриваемой  модели  переходом  от  изотропного  протекания  к  направленному  [1;  2].  Данный  эффект  выразителен  при  условии  достаточно  больших  размеров  кластера  локализованных  состояний,  что  проявляется  в  усилении  зависимости  нестационарной  проводимости  диэлектрика  от  напряженности  электрического  поля  с  увеличением  длительности  нагружения.

Согласно  теории  нестационарной  прыжковой  электропроводности  [2],  зависимость  проводимости  от  времени  и  напряженности  поля  имеет  вид: 

,

где:  ; 

  —  вероятность  критического  прыжка,  определяющего  момент  возникновения  проводящего  кластера,  замыкающего  электроды  (установления  статической  проводимости); 

  —  величина  размерности  проводимости,  равная  по  порядку  величины  статической  проводимости  материала  .

Представленная  на  рисунке  2  (сплошная  кривая)  линеаризация  экспериментально  полученной  зависимости  в  координатах,  отвечающих  приведенной  формуле,  обнаруживает  хорошее  соответствие  прогнозу  теории  (штриховая  линия).

Рисунок  2.  Линеаризация  временной  зависимости  проводимости  оксида  тантала  при  напряженности  электрического  поля  6×10⁵  В/см

Используя  рассматриваемую  модель,  из  экспериментальных  данных,  представленных  на  рисунке  2,  может  быть  восстановлена  вероятность  критического  прыжка  в  зависимости  от  напряженности  поля  . 

Полученная  зависимость  хорошо  соответствует  наблюдаемому  поведению  статической  проводимости  металлооксида  в  области  сильных  электрических  полей  (рис.  3). 

Рисунок  3.  Зависимость  проводимости  оксида  тантала  от  напряженности  электрического  поля  при  различных  температурах  э  298  К  (1),  323  К  (2),  343  К  (3),  363  К  (4)

Представленная  на  рисунке  3  зависимость  статической  проводимости  от  напряженности  электрического  поля  описывается  аналитическим  выражением  для  неомической  прыжковой  электропроводности:  ,  где    —  проводимость  материала  в  омической  области  напряжений;

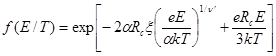
Здесь    —  радиус  локализации  электронных  состояний;    —  длина  прыжка;    —  критический  индекс,    —  численный  коэффициент.

Указанные  выражения  дают  основание  для  восстановления  из  экспериментальных  данных  концентрации  и  радиуса  локализации  состояний,  по  которым  осуществляется  транспорт.

Еще  одним  подтверждением  правомерности  предлагаемого  подхода  является  экспериментально  установленное  усиление  температурной  зависимости  нестационарной  проводимости  с  увеличением  длительности  электрического  нагружения  (рис.  4). 

Рисунок  4.  Температурная  зависимость  нестационарной  (1,2)  и  статической  проводимости  (3)  оксида  тантала.  Длительность  электрического  нагружения  оксида  60  с  (1);  3,6×103  с  (2);  более  105  с  (3)

Этот  факт  укладывается  в  рамки  рассматриваемой  картины  прыжкового  транспорта  носителей  заряда,  если  допустить,  что  вероятность  определяющего  проводимость  прыжка  уменьшается  с  увеличением  его  энергии  активации.  При  этом  статической  проводимости,  определяемой  вероятностью  критического  прыжка,  должна  соответствовать  максимальная  энергия  активации.

Список  литературы :

1.Ханин  С.Д.  Электронные  свойства  аморфных  диэлектрических  оксидов  металлов.  —  В  кн.  «Физика  неупорядоченных  и  наноструктурированных  оксидов  и  халькогенидов  маталлов»:  Монография  /  Под  ред.  Г.А.  Бордовского.  СПб.:  Изд-во  РГПУ  им.  А.И.  Герцена.  —  2011.  —  с.  69—104.

2.Böttger  H.  Hopping  Conduction  in  Solids.  /  H.  Böttger,  V.  Bryksin  —  1985.  —  VCH.  —  420  p.