ПРИМЕНЕНИЕ  АЛГОРИТМА  ПОСЛЕДОВАТЕЛЬНОЙ  РАСКРАСКИ  ГРАФА  В  СОТОВОЙ  СЕТИ

Мурзаков  Денис  Эрионович

студент  3  курса,  кафедра  геоинформатики  и  информационной  безопасности,  СГАУ  им.  Королёва,  РФ,  г.  Самара

Е-mail :  Murzakov.d@gmail.com

Зенков  Михаил  Андреевич

студент  3  курса,  кафедра  геоинформатики  и  информационной  безопасности,  СГАУ  им.  Королёва,  РФ,  г.  Самара

Е-mail :  zenkovma94@gmail.com

Жуков  Александр  Дмитриевич

студент  3  курса,  кафедра  геоинформатики  и  информационной  безопасности,  СГАУ  им.  Королёва,  РФ,  г.  Самара

Е-mail:  alexzhuk163@gmail.com

Тишин  Владимир  Викторович

доцент,  кафедра  прикладной  математики,  СГАУ  им.  Королёва,  РФ,  г.  Самара

USE  OF  ALGORITHM  OF  SEQUENTIAL  COLORING  OF  DIAGRAM  IN  CELLULAR  NETWORK

Denis  Murzakov

3-year  student,  Geoinformatics  and  Information  Security  Chair,  Samara  State  Aerospace  University  named  after  Korolev,  Russia,  Samara

Mikhail  Zenkov

3-year  student,  Geoinformatics  and  Information  Security  Chair,  Samara  State  Aerospace  University  named  after  Korolev,  Russia,  Samara

Aleksandr  Zhukov

3-year  student,  Geoinformatics  and  Information  Security  Chair,  Samara  State  Aerospace  University  named  after  Korolev,  Russia,  Samara

Vladimir  Tishin

associate  professor,  Applied  Mathematics  Chair,  Samara  State  Aerospace  University  named  after  Korolev,  Russia,  Samara

АННОТАЦИЯ

В  данной  статье  рассматривается  проблема  распределения  диапазонов  частот  в  системах  сотовой  связи.  Показано  решение  с  помощью  теории  графов.  Продемонстрирован  алгоритм  последовательной  раскраски  графа.

ABSTRACT

The  article  deals  with  the  problem  of  the  distribution  of  frequency  bands  in  the  cellular  network.  Solution  is  shown  with  the  help  of  diagram  theory.  Algorithm  of  sequential  diagram  coloring  is  demonstrated. 

Ключевые  слова:  приложение  теории  графов;  алгоритм  раскраски  графа;  последовательная  раскраска;  сотовая  связь;  распределение  частотных  диапазонов.

Keywords:  attachment  of  diagram  theory;  algorithm  of  diagram  coloring;  sequential  coloring;  cellular  network;  distribution  of  frequency  bands. 

Введение

Сотовая  связь  —  один  из  видов  мобильной  радиосвязи,  в  основе  которого  лежит  сотовая  сеть.  Общая  зона  покрытия  делится  на  ячейки  (соты),  определяющиеся  зонами  покрытия  отдельных  базовых  станций.  Соты  частично  перекрываются  и  вместе  образуют  сеть.  На  ровной  поверхности  без  застройки  зона  покрытия  одной  базовой  станции  представляет  собой  круг,  поэтому  составленная  из  них  сеть  имеет  вид  шестиугольных  ячеек. 

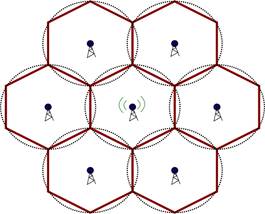
Рисунок  1.  Зоны  покрытия  БС

Из-за  ограниченного  числа  диапазонов  частот,  которые  могут  использоваться  в  системе  мобильной  радиосвязи,  нельзя  исключить  использование  различными  базовыми  станциями  одинаковых  диапазонов,  в  результате  чего  возникают  взаимные  помехи.  Распределение  частот  между  отдельными  базовыми  станциями  поэтому  должно  осуществляться  таким  образом,  чтобы  обеспечить  максимально  свободную  от  взаимных  помех  работу  систем  мобильной  радиосвязи.  На  Рис.  2.  тремя  разными  цветами  обозначены  три  разных  диапазона  частот  базовых  станций.

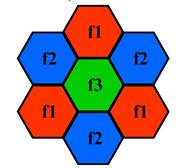
Рисунок  2.  Частотные  диапазоны  базовых  станций

Количество  абонентов,  обслуживаемых  базовой  станцией  в  определенный  момент  времени,  напрямую  зависит  от  ширины  её  канала.  Поэтому  эффективнее  использовать  наименьшее  число  различных  частотных  диапазонов,  тем  самым  увеличивая  их  ширину.  На  Рис.  3.  приведен  пример  неэффективного  использования  частотных  диапазонов. 

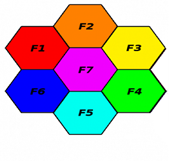
Рисунок  3.  Частотные  диапазоны  базовых  станций

Цель  нашей  работы  —  Распределить  частотный  диапазон  между  базовыми  станциями  таким  образом,  чтобы  минимизировать  помехи,  оказываемые  станциями  друг  на  друга.

Для  достижения  нашей  цели  были  поставлены  следующие  задачи:

1.  Построить  граф  согласно  структуре  сети.

2.  Применить  алгоритм  последовательной  раскраски  к  полученному  графу.

3.  Распределить  частотный  диапазон  в  соответствии  с  результатами  раскраски

Алгоритм  последовательной  раскраски  графа

1.  Упорядочить  вершины  по  невозрастанию  степени.

2.  Окрасить  первую  вершину  в  цвет  1.

3.  Выбрать  цвет  окраски  1.

4.  Пока  не  окрашены  все  вершины,  повторять:

4.1.Окрасить  в  выбранный  цвет  всякую  вершину,  которая  не  смежна  с  другой,  уже  окрашенной  в  этот  цвет.

4.2. Выбрать  следующий  цвет.

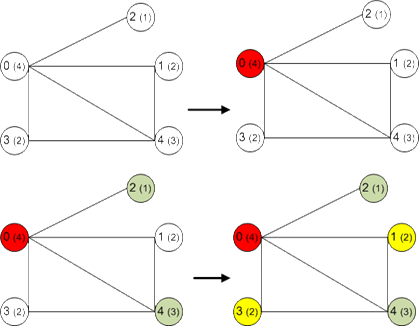
Рисунок  4.  Работа  алгоритма

Применение  алгоритма

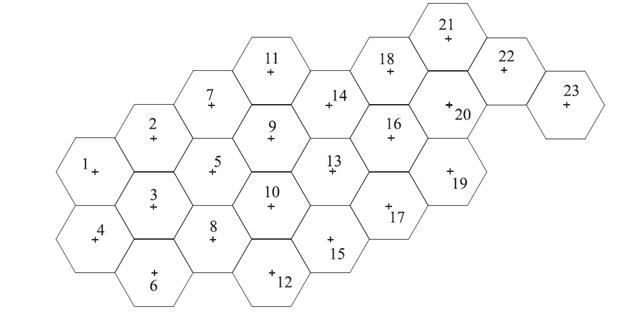
Рисунок  5.  Рассматриваемая  сеть

Данные  и  необходимые  расчеты:

•    Для  базовых  станций  радиус  зон  покрытия  базовых  станций  равен  3  км,  координационное  расстояние  —  9,2  км.

•    Вычислим  расстояние  до  ближайших  станций:

  r1=r(1;2)=r(1;3)=r(1;4)=R0=3√3≈5,1;

  r2=r(1;5)=r(1;6)=3Rзоны=9;

  r3=r(1;7)=r(1;8)=2R0≈10,3;

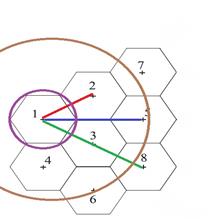
Рисунок  6.  Расстояния  между  станциями

Представим  сеть  в  виде  графа:

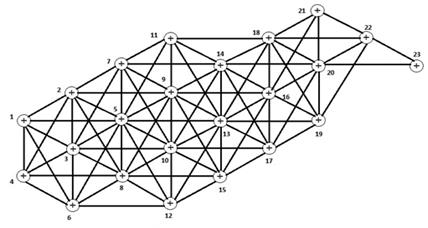
Рисунок  7.  Граф

Первый  шаг:

Степени  вершин:

11:  5,13;

10:  9,10;

9:  8,14,16;

8:  3,18,20;

7:  2,7,15,17;

6:  6,11,12,19;

5:  1,4,22;

4:  21;

2:  23;

Выделяем  первое  независимое  множество:

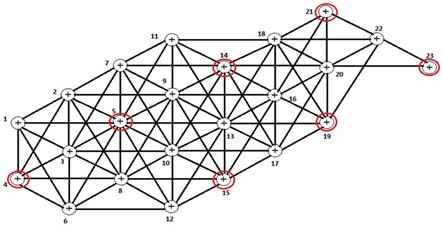
Рисунок  8.  Выделяем  первое  независимое  множество

Получаем  следующий  граф: 

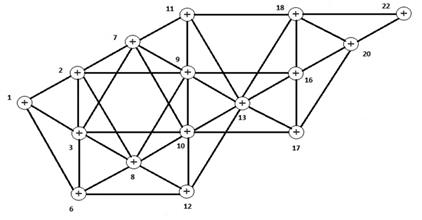
Рисунок  9.  Новый  граф

Второй  шаг:

Оставшиеся  вершины  и  их  степени:

11:  13;

10:  9,10;

9:  8,16;

8:  3,18,20;

7:  2,7,17;

6:  6,11,12;

5:  1,22;

Выделяем  второе  независимое  множество:

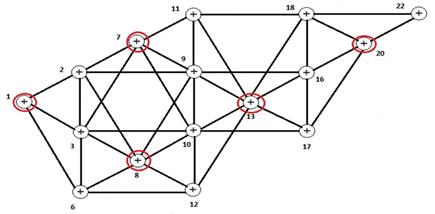
Рисунок  10.  Выделяем  второе  независимое  множество

Получаем  следующий  граф:

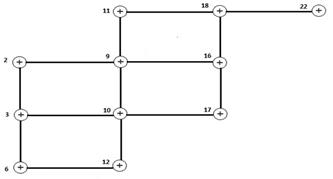
Рисунок  11.  Новый  граф

Третий  шаг:

Оставшиеся  вершины  и  их  степени:

10:  9,10;

9:  16;

8:  3,18;

7:  2,17;

6:  6,11,12;

5:  22;

Выделяем  третье  независимое  множество:

Рисунок  12.  Выделяем  третье  независимое  множество

Окончательно  получаем  граф  вида:

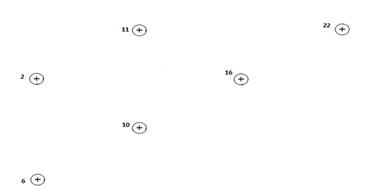
Рисунок  13.  Новый  граф

Группы  базовых  станций:

•    1  группа:  4,5,14,15,19,21,23;

•    2  группа:  1,7,8,13,20;

•    3  группа:  3,9,12,17,18;

•    4  группа:  2,6,10,11,16,22;

Согласно  результатам  проводим  раскраску:

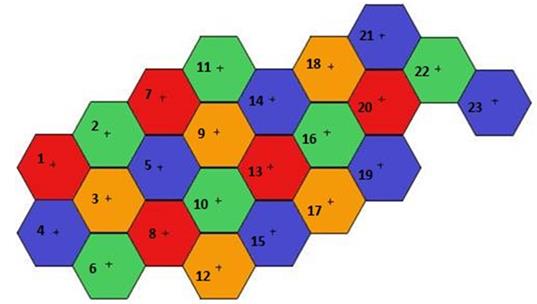
Рисунок  14.  Результат

Согласно  результатам  работы  алгоритма,  если  для  оператора  сотовой  связи  выделены  следующие  диапазоны  частот:  1770,1—1798,7  МГц.  Итого  28,6  МГц,  тогда:

1.  1770,1—1777,25  (МГц).

2.  1177,25—1784,4  (МГц).

3.  1784,4—1791,55  (МГц).

4.  1791,55—1798,7  (МГц).

Заключение:

Теория  графов  позволяет  решать  огромное  количество  практических  задач,  включая  и  нашу  исходную  задачу,  которой  мы  посвятили  эту  работу,  а  именно  применение  алгоритма  последовательной  раскраски  графа  в  сотовой  сети.

Для  достижения  нашей  цели  были  выполнены  следующие  задачи:  построен  граф,  согласно  структуре  сети;  Применен  алгоритм  последовательной  раскраски  к  полученному  графу;  Распределен  частотный  диапазон  в  соответствии  с  результатами  раскраски.

Список  литературы:

1.Алгоритм  раскраски  графа  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://urban-sanjoo.narod.ru/colours.html001  (дата  обращения  20.04.2015).

2.Додонова  Н.Л.  Конспект  лекций  по  дисциплине  теория  конечных  графов  и  ее  применения  Самара:  2010  —  с.  52.

3.Носов  В.И.,  Бернштейн  Т.В.  Элементы  теории  графов.  Учебное  пособие.  Новосибирск,  2008.  —  107  с.

4.Принцип  повторного  использования  частот  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://afu.com.ua/gsm/princip-povtornogo-ispolzovaniya-chastot  (дата  обращения  20.04.2015).

5.Сотовая  связь  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://klin-gsm.ru/index.php?id=001  (дата  обращения  20.04.2015).