О  Τ-ЗАМКНУТЫХ  N -КРАТНО  Ω-БИКАНОНИЧЕСКИХ  ФОРМАЦИЯХ  КОНЕЧНЫХ  ГРУПП

Сорокина  Марина  Михайловна

канд.  физ.-мат.  наук,  доцент  Брянского  государственного  университета,  РФ,  г.  Брянск

E -mail: 

Петрушин  Павел  Викторович

магистрант  направления  «Математика»  физико-математического  факультета  Брянского  государственного  университета,  РФ,  г.  Брянск

ON  Τ-CLOSED  N-MULTIPLY  Ω-BICANONICAL  FORMATIONS  OF  FINITE  GROUPS

Sorokina  Marina

candidate  of  Physical  and  Mathematical  Sciences,  assistant  professor  of  Bryansk  State  University,  Russia,  Bryansk

Petrushin  Pavel

undergraduate  of  Mathematics  Direction  of  Faculty  of  Physics  and  Mathematics  of  Bryansk  State  University,  Russia,  Bryansk

АННОТАЦИЯ

Работа  посвящена  исследованию  Ω-расслоенных  формаций  конечных  групп.  Свойства  таких  формаций  зависят  от  свойств  двух  описывающих  их  функций:  Ω-спутника  и  направления.  Целью  данной  статьи  является  исследование  свойств  Ω-биканонических  формаций,  которые  представляют  один  из  видов  Ω-расслоенных  формаций.  При  исследовании  используются  методы  доказательств  теории  классов  групп.  В  статье  установлена  взаимосвязь  между  τ-замкнутостью  -кратно  Ω-биканонической  формации  и  τ-замкнутостью  ее  -спутника. 

ABSTRACT

This  article  is  devoted  to  Ω-foliated  formations  of  finite  groups.  Properties  of  such  formations  depend  on  the  properties  of  the  two  functions  which  describe:  Ω-satellite  and  direction.  The  purpose  of  this  paper  is  to  study  the  properties  of  Ω-bicanonical  formations,  which  are  a  type  of  Ω-foliated  formations.  In  the  study  used  methods  of  proof  of  the  theory  of  classes  of  groups.  In  this  article  there  has  been  established  a  connection  between  τ-closure  of  n-multiply  Ω-bicanonical  formation  and  τ-closure  of  its  -satellite. 

Ключевые  слова:   конечная  группа;  класс  групп;  формация  групп;  Ω-расслоенная  формация;  Ω-биканоническая  формация;  подгрупповой  функтор.

Keywords:   a  finite  group;  a  class  of  groups;  a  formation  of  groups;  Ω-foliated  formation;  Ω-bicanonical  formation;  a  subgroup  functor.

В  современной  теории  классов  групп  центральное  место  занимают  формации  конечных  групп,  введенные  в  рассмотрение  В.  Гашюцем  в  1963  году  [8].  Важнейшие  результаты  о  формациях  конечных  групп  представлены  в  монографии  Л.А.  Шеметкова  [7].  В  теории  формаций  конечных  групп  большую  роль  играют  функциональные  методы.  Так,  например,  наиболее  изученные  в  настоящее  время  локальные  и  композиционные  формации  построены  с  помощью  специальных  функций  —  экранов  [7].  В  1999  году  В.А.  Ведерниковым  был  разработан  новый  функциональный  подход  к  исследованию  классов  групп,  при  котором  формации  (названные  в  [1]  Ω-расслоенными)  строятся  с  помощью  двух  сопутствующих  функций  —  функции-спутника  (аналог  экрана)  и  функции-направления  [1].  Важным  видом  Ω-расслоенных  формаций  являются  Ω-биканонические  формации,  изучаемые  в  данной  статье.

В  ходе  исследований  (см.,  например  [1;  9])  было  выявлено,  что  свойства  Ω-расслоенных  формаций  во  многих  случаях  зависят  от  свойств  их  спутников.  В  работе  [4]  получены  результаты  о  спутниках  τ-замкнутых  Ω-расслоенных  формаций.  В  [7]  была  исследована  взаимосвязь  между  τ-замкнутостью  n-кратно  Ω-расслоенной  формации  и  τ-замкнутостью  ее  -спутника  в  случае,  когда  .  Данная  работа  продолжает  исследования  в  этом  направлении  для  Ω-биканонических  формаций  и  произвольного  класса  простых  групп  .

Рассматриваются  только  конечные  группы.  Используются  определения  и  обозначения,  принятые  в  [1;  9].  Приведем  лишь  некоторые  из  них.  Пусть    —  класс  всех  конечных  простых  групп,    —  класс  всех  простых  групп,  изоморфных  композиционным  факторам  группы  ;    —  объединение  классов    для  всех  ,  Ω  —  непустой  подкласс  класса  ,    —  класс  всех  конечных  Ω-групп,  т.е.  таких  групп,  что  . 

Функция  {формации  групп}  называется  ΩF-функцией;  функция  {непустые  формации  Фиттинга}  называется  FR-функцией.  Функции    и    принимают  одинаковые  значения  на  изоморфных  группах  из  области  определения  [1,  с.  126].  Формация 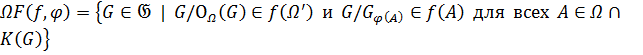   называется  Ω-расслоенной  формацией  с  Ω-спутником    и  направлением    [1,  с.  127].  Формация    называется  Ω-биканонической,  или,  коротко,  ΩB-формацией,  если    для  любой  абелевой  группы    и    для  любой  неабелевой  группы  ,  и  обозначается    [1,  с.  129].  Направление  Ω-биканонической  формации  обозначается  через  .

Пусть  ,    —  некоторая  FR-функция.  Всякая  формация  считается  0-кратно  Ω-расслоенной  формацией  с  направлением  .  При    формация    называется  n-кратно  Ω-расслоенной  с  направлением  ,  или,  иначе,  -расслоенной  формацией,  если    обладает  -спутником,  т.  е.  таким  Ω-спутником,  всякое  значение  которого  является  -кратно  Ω-расслоенной  формацией  с  направлением  φ  [9,  с.  218].  n-кратно  Ω-биканоническую  формацию  кратко  будем  называть  -биканонической.

Пусть  τ  —  отображение,  которое  ставит  в  соответствие  всякой  группе    некоторую  систему    ее  подгрупп.  Отображение  τ  называется  подгрупповым  функтором,  если    для  любого  изоморфизма    каждой  группы    [3,  с.  13].  Подгрупповой  функтор  τ  называется  регулярным,  если  выполняются  два  условия:  1)  ,  ;  2)    [2,  с.  14].  Подгрупповой  функтор  τ  называется  Ω-радикальным,  если  для  любой  группы    и  для  любой    справедливо  ;  φ-радикальным,  если  для  любой  группы    и  для  любой    для  всех    выполняется  ;  Ωφ-радикальным,  если    является  Ω-радикальным  и  -радикальным,  где  φ  —  некоторая  FR-функция  [3,  с.  76].  Подгрупповой  функтор  τ  называется  замкнутым  относительно  композиционных  факторов,  если  для  любой    справедливо  включение    для  каждой  группы    [4,  с.  76].

Формация    называется  τ-замкнутой,  если    для  любой  группы    [5,  с.  23].  Ω-спутник  Ω-расслоенной  формации    называется  τ-замкнутым,  если  все  его  значения  являются  τ-замкнутыми  формациями.

В  следующей  теореме  устанавливается  взаимосвязь  между  τ-замкнутостью  -кратно  Ω-биканонической  формации  и  τ-замкнутостью  ее  -спутника.

Теорема  1.  Пусть    —  Ω-биканоническая  формация,  τ  —  регулярный  Ω-радикальный  подгрупповой  функтор,  замкнутый  относительно  композиционных  факторов,  .  Тогда  формация    является  τ-замкнутой  -биканонической  формацией  в  том  и  только  том  случае,  когда    обладает  хотя  бы  одним  τ-замкнутым  -спутником.

Доказательство.  Необходимость.  Пусть    —  τ-замкнутая  -биканоническая  формация.  По  следствию  12  [9,  с.  224]    имеет  единственный  максимальный  внутренний  Ω-спутник  ,  причем    для  всех    и    для  всех  ,  где    —  произвольный  внутренний  Ω-спутник  формации  .  Поэтому  для  любого    формация    является  τ-замкнутой,  а  согласно  лемме  2.1  [6,  с.  26]  —  -биканонической  формацией.

Пусть  .  Покажем,  что    —  τ-замкнутая  -биканоническая  формация.  Согласно  доказательству  леммы  2  [3,  с.  77],    —  τ-замкнутая  формация.  Покажем,  что    —  -биканоническая  формация.  Так  как    —  -каноническая  формация,  то    обладает  -спутником  .  Пусть    —  ΩF-функция,  такая,  что    для  всех  .  Согласно  лемме  4  [1,  с.  128],    является  Ω-спутником  формации  .  Так  как  по  лемме  2.1  [6,  с.  26]    является  -биканонической  формацией,  то  по  лемме  2.4  [6,  с.  27]    —  -биканоническая  формация  для  любого  .  Таким  образом,  Ω-спутник    формации    является  -спутником.  Кроме  того,  по  лемме  2.3  [6,  с.  27]  формация    является  -биканонической.  Тогда,  согласно  теореме  5.38  [4,  с.  191]  и  следствию  9  [2,  с.  223],    —  -биканоническая  формация.  Из  строения    следует,  что    является  внутренним  Ω-спутником  формации  ,  и  поэтому  .  Тем  самым  установлено,  что    —  τ-замкнутый  -спутник  формации  .

Достаточность.  Пусть    —  τ-замкнутый  -спутник  формации  ,    и  .  Покажем,  что  .  Так  как  ,  то    для  любой  абелевой  группы    и    для  любой  неабелевой  группы  .  Поскольку    и  τ  —  подгрупповой  функтор,  замкнутый  относительно  композиционных  факторов,  то  ,  и  значит,    для  любой  абелевой  группы  .  Пусть  .  Из  ,  ввиду  регулярности  подгруппового  функтора  τ,  получаем  .  Отсюда,  в  силу  τ-замкнутости  формации  ,  следует,  что  .  Так  как  подгрупповой  функтор  τ  является  -радикальным  и  ,  то    и  .  Аналогично  рассуждая,  получаем,  что    для  любой  неабелевой  группы  .  Далее,  из  ,    и  τ-замкнутости  формации    имеем  .  Так  как  τ  —  Ω-радикальный  подгрупповой  функтор,  то    и  .  Таким  образом,  по  определению  Ω-биканонической  формации,  ,  и  значит,  формация    является  τ-замкнутой.  Согласно  определению  n-кратно  Ω-расслоенной  формации,    —  -биканоническая  формация.  Теорема  доказана.

Список  литературы:

1.Ведерников  В.А.,  Сорокина  М.М.  Ω-расслоенные  формации  и  классы  Фиттинга  конечных  групп  //  Дискретная  математика.  —  Т.  13.  —  Вып.  3,  —  2001.  —  С.  125—144.

2.Каморников  С.Ф.,  Селькин  М.В.  Подгрупповые  функторы  и  классы  конечных  групп.  Минск:  Беларуская  навука,  2003.  —  254  с.

3.Корпачева  М.А.,  Сорокина  М.М.  Критические  Ω-расслоенные  τ-замкнутые  формации  конечных  групп  //  Вестник  Брянского  государственного  университета.  №  4:  Точные  и  естественные  науки.  Выпуск  2.  —  Брянск:  РИО  БГУ,  2012.  —  С.  75—79.

4.Монахов  В.С.  Введение  в  теорию  конечных  групп  и  их  классов.  Минск:  Вышэйшая  школа,  2006.  —  207  с.

5.Скиба  А.Н.  Алгебра  формаций.  ‒  Минск:  Беларуская  навука,  1997.  —  240  с.

6.Сорокина  М.М.,  Петрушин  П.В.  О  спутниках  τ-замкнутых  n-кратно  Ω-расслоенных  формаций  конечных  групп  //  Молодой  ученый.  —  №  10  (90),  —  2015.  —  С.  24—30. 

7.Шеметков  Л.А.  Формации  конечных  групп.  М.:  Наука,  1978.  —  272  с.

8.Gaschütz  W.  Zur  Theorie  der  endlichen  auflösbaren  Gruppen.  Math.  Z.,  —  1963.  —  Vol.  80,  —  №  4.  —  S.  300—305.

9.Vedernikov  V.A.  Maximal  satellites  of  Ω-foliated  formations  and  Fitting  classes  //  Proc.  Steklov  Inst.  Math.  —  №  2,  —  2001.  —  P.  217—233.