Статья опубликована в рамках: XXX Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 06 мая 2015 г.)
Наука: Математика
Секция: Вещественный, комплексный и функциональный анализ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
О РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИОНАЛЬНЫХ РЯДОВ
Зикеева Марина Кареновна
студент Московского государственного университета информационных технологий, радиотехники и электроники, РФ, г. Серпухов
E -mail: zikeeva.marina@yandex.ru
Таперечкина Вера Алексеевна
канд. физ.-мат. наук, доцент Московского государственного университета информационных технологий, радиотехники и электроники, РФ, г. Серпухов
UNIFORM CONVERGENCE OF FUNCTIONAL SEQUENCES AND FUNCTIONAL SERIES
Marina Zikeeva
student of Moscow State University of Information Technologies, Radio Engineering and Electronics, Russia, Serpukhov
Vera Taperechkina
candidate of Physical and Mathematical Sciences, associate professor of Moscow State University of Information Technologies, Radio Engineering and Electronics, Russia, Serpukhov
АННОТАЦИЯ
В работе рассматриваются функциональные свойства равномерно сходящихся функциональных последовательностей и функциональных рядов. Подробно разобраны различные примеры и контрпримеры, демонстрирующие эти свойства.
ABSTRACT
The functional properties of uniformly convergent functional sequences and functional series are considered in this study. Various examples and counterexamples demonstrating these properties have been discussed in detail.
Ключевые слова: равномерная сходимость; функциональные последовательности; функциональные ряды.
Keywords: uniform convergent; functional sequences; functional series.
1. Поточечная сходимость функциональной последовательности
Функциональной последовательностью называется занумерованное множество функций {fn(x)}, имеющих одну и ту же область определения D∈R. При этом множество D называется областью определения функциональной последовательности {fn(x)}.
Пусть∀х0∈EÌD последовательность {fn(x0)} имеет конечный предел, f(x0), т. е. ∀ ε Ǝ номер N= N(ε,x0):∀n>N=>|fn(x0)![]() f(x0)|< ε.
f(x0)|< ε.
Определенная таким образом сходимость называется поточечной, и пишут ![]() fn(x0)= f(x0).
fn(x0)= f(x0).
Так как ∀x∈E (E-множество сходимости последовательности) определено число f(x), то ![]() fn(x) представляет собой функцию, которая называется предельной функцией последовательности {fn(x)}.
fn(x) представляет собой функцию, которая называется предельной функцией последовательности {fn(x)}.
Нас будут интересовать функциональные свойства предельной функции f(x) = ![]() fn(x) в зависимости от свойств fn(x) и от «качества» сходимости последовательности {fn(x)}. Например, следует ли из непрерывности в fn(x) непрерывность предельной функции.
fn(x) в зависимости от свойств fn(x) и от «качества» сходимости последовательности {fn(x)}. Например, следует ли из непрерывности в fn(x) непрерывность предельной функции.
Приведем несколько примеров.
Пример 1 [3]/
Пусть fn(x) = xn, n — натуральное, D= [0,1]. Найти предельную функцию.
Решение.
fn(0) = 0,![]() fn(0) = 0, fn(1) =1,
fn(0) = 0, fn(1) =1, ![]() fn(1) = 1,
fn(1) = 1,
При 0<x<1,fn(x) = xn. Покажем по определению, что ![]() fn(x) = 0.
fn(x) = 0.
Пусть дано ∀ε >0. Неравенство | xn– 0| <e выполняется при |x|n<ε,
![]() (причем
(причем![]() n>
n>![]() . Обозначим N = [
. Обозначим N = [![]() +1.
+1.
Таким образом, ∀ ε найдется номер N, такой, что ∀n>N выполняется неравенство |xn![]() 0 |< ε, а значит, что
0 |< ε, а значит, что ![]() fn(x) = 0
fn(x) = 0
Итого предельная функция f(x) =![]() E =[0,1] — множество сходимости.
E =[0,1] — множество сходимости.
Функции fn(x) = xn непрерывны на E, однако, предельная функция имеет в точке x = 1 разрыв первого рода со скачком.
Пример 2 [1].
fn(x) = ![]() ; D = [0,1]. Найти предельную функцию.
; D = [0,1]. Найти предельную функцию.
Решение.
fn(0) = 1; ![]() fn(0) = 1. Для ∀x∈ (0,1] имеем f(x) =
fn(0) = 1. Для ∀x∈ (0,1] имеем f(x) = ![]() .
.
Итого, предельная функция f(x) = ![]() ; E =[0,1] — множество поточечной сходимости.
; E =[0,1] — множество поточечной сходимости.
Функции fn(x) = ![]() непрерывны на [0,1], а предельная функция f(x) имеет в точке x = 0 разрыв первого рода со скачком.
непрерывны на [0,1], а предельная функция f(x) имеет в точке x = 0 разрыв первого рода со скачком.
Пример 3.
fn(x) = ![]() ; D = [0,1]. Найти предельную функцию.
; D = [0,1]. Найти предельную функцию.
Решение.
Если x = 0, то fn(0)= ![]() ,
, ![]() fn(0)=
fn(0)= ![]() .
.
Для x∈(0,1] предельную функцию найдем, используя правило Лопиталя.
f(x) = ![]() =
= ![]() ∀x ≠0).
∀x ≠0).
Итого, предельная функция f(x) = 0, ∀x∈[0,1]. E=[0,1] — множество поточечной сходимости.
Функции fn(x) = ![]() непрерывны на [0,1] и предельная функция f(x) =0 непрерывна на [0,1].
непрерывны на [0,1] и предельная функция f(x) =0 непрерывна на [0,1].
Пример 4.
fn(x) = ![]() ; D= [0,1]. Найти предельную функцию.
; D= [0,1]. Найти предельную функцию.
Решение.
f(x) = ![]() fn(x)=
fn(x)= ![]() = 0 ; ∀x∈[0,1].
= 0 ; ∀x∈[0,1].
Итого, предельная функция f(x)=0. E=[0,1] — множество поточечной сходимости.
Функции fn(x) = ![]() непрерывны на [0,1] и предельная функция f(x) =0 непрерывна на [0,1].
непрерывны на [0,1] и предельная функция f(x) =0 непрерывна на [0,1].
Пример 5.
fn(x) = 2![]() ; D = [0,1]. Найти предельную функцию.
; D = [0,1]. Найти предельную функцию.
Решение.
Для x∈[0,1] предельную функцию найдем, используя правило Лопиталя.
f(x) = ![]()
Итого, предельная функция f(x)=0 на [0,1].E=[0,1] – множество поточечной сходимости.
Функции fn(x) = ![]() непрерывны на [0,1] и предельная функция f(x)=0 непрерывна на [0,1].
непрерывны на [0,1] и предельная функция f(x)=0 непрерывна на [0,1].
2. Равномерная сходимость функциональной последовательности
Последовательность {fn(x)} называется равномерно сходящейся на множестве E, если
∀ ε > 0 Ǝ номер N = N(ε) :∀n>N => |fn(x)![]() f(x)|<ε .
f(x)|<ε .
Отличие этого определения от прежнего определения состоит в том, что для любого ε > 0 требуется существование номера N, зависящего только от ε, но не зависящего от x, то есть общего для всего множества Е.
Графически, равномерная сходимость последовательности {fn(x)} к предельной функции f(x) состоит в приближении графиков fn(x) с ростом номера n к графику f(x)на всем множестве E. Это заведомо справедливо, если потребовать, чтобы![]() |fn(x)
|fn(x)![]() f(x)|= 0, то есть, начиная с некоторого номера N
f(x)|= 0, то есть, начиная с некоторого номера N ![]() |fn(x)
|fn(x)![]() f(x)| <ε, а тогда, разумеется, ∀x
f(x)| <ε, а тогда, разумеется, ∀x![]() справедливо, что |fn(x)
справедливо, что |fn(x)![]() f(x)| <ε.
f(x)| <ε.
Исследование на равномерную сходимость напоминает решение задачи с параметром, если в качестве параметра принять x.
Рассмотрим детально приведенные выше примеры с точки зрения определения равномерной сходимости, используя полученные результаты.
К примеру 1.
fn(x) = xn; E = [0,1] ; Ранее было полученоf(x) = ![]()
∀![]() |fn(x)
|fn(x)![]() f(x)| <ε; при ∀n >N(ε, x) = [
f(x)| <ε; при ∀n >N(ε, x) = [![]() ] + 1.
] + 1.
Отметим, что N = N(ε, x), зависит от x. Причем, чем ближе х к 1, тем больше N(ε, x) и, тем самым, не существует такого N = N(ε), которое пригодно для ∀x∈[0,1].
Рисунок 2.1 иллюстрирует характер приближения графиков fn(x) к графику предельной функции f(x). Предельная функция изменяется в x=1 скачком и f(1) = 1, а максимумы всех функций fn(x) остаются неподвижными, fn(1) = 1.
На Рисунке 2.1 изображена поточечная сходимость при x0 =0,9 и ε = 0,1,
N = [![]() +1 = [
+1 = [![]() +1= 30, |f30(x0)
+1= 30, |f30(x0)![]() f(x0)| = |0,930
f(x0)| = |0,930 ![]() 0| = 0,0424<0,1.
0| = 0,0424<0,1.
Итак, функциональная последовательность непрерывных функций {xn} сходится к разрывной функции f(x) поточечно, но неравномерно. Отметим, что, если E = [0,r], где r<1, то сходимость равномерная, N(ε) = [![]() ] + 1.
] + 1.
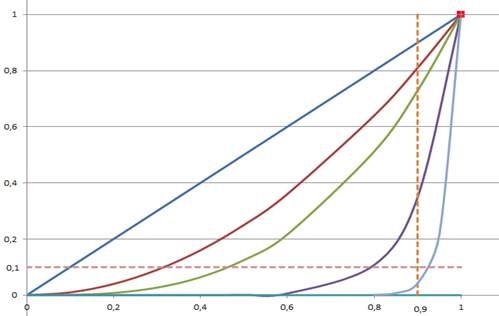
Рисунок 2.1. Пример неравномерной сходимости последовательности {xn }
К примеру 2.
fn(x) = ![]() ; E= [0,1]. Ранее было получено f(x) =
; E= [0,1]. Ранее было получено f(x) = ![]()
|fn(x)![]() f(x)| =
f(x)| = ![]() ,
, ![]() <ε,
<ε, ![]() >
>![]() , n>
, n>![]() N = N(ε, x) = [
N = N(ε, x) = [![]() .
.
Поточечная сходимость на E есть. Однако, при x![]() 0 получаем
0 получаем ![]() .
.
Следовательно, не существует единого N(ε), пригодного для всего отрезка [0,1].
Итак, сходимость неравномерная. Аналогично Примеру 1, если E = [r,1], где r>0, то сходимость равномерная, N(ε) = [![]() .
.
Приведем иллюстрацию к Примеру 2.
Графики функций fn(x) = ![]() на множестве действительных чисел представляют собой семейство гипербол с разрывом при 1 + nx = 0, то есть
на множестве действительных чисел представляют собой семейство гипербол с разрывом при 1 + nx = 0, то есть
x = - ![]() .
.
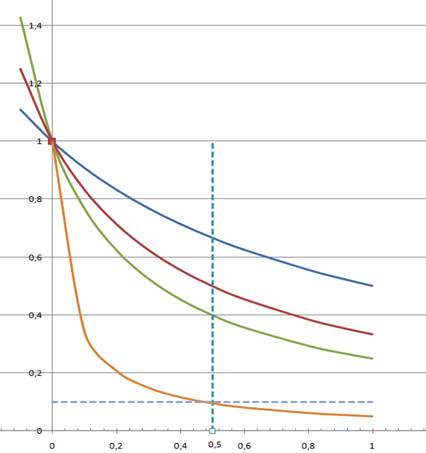
Рисунок 2.2. Пример неравномерной сходимости последовательности {![]() }
}
На Рисунке 2.2 представлены графики правой ветви четырех функций: f1(x), f2(x), f3(x), f19(x) и предельной функции f(x). Если, например, ε = 0,1 ,
x0 = 0,5, то срезом является монотонно убывающая последовательность {fn(0,5)}={![]() }и N(ε) = [
}и N(ε) = [![]() = 19,
= 19,
|f19(0,5)![]() f(0,5)| = |
f(0,5)| = |![]() | =
| = ![]() = 0,095 < 0,1.
= 0,095 < 0,1.
Все графики fn(x) при n≥ 19 в точке x0 = 0,5, расположены к графику предельной функции ближе, чем ε = 0,1.
Но, если, например, ε = 0,1 , x0 = 0,1, то получим N(ε) = 91, |f91(0,1)![]() f(0,1)| = |
f(0,1)| = |![]() | =
| = ![]() = 0,099 < 0,1 и чем ближе x0 к нулю, тем большее N следует взять в определении поточечной сходимости и невозможно указать N(ε) единого для всех x отрезка [0,1].
= 0,099 < 0,1 и чем ближе x0 к нулю, тем большее N следует взять в определении поточечной сходимости и невозможно указать N(ε) единого для всех x отрезка [0,1].
Итак, имеем неравномерную сходимость непрерывных функций fn(x) к разрывной функции f(x).
К примеру 3.
fn(x) = ![]() ; E = [0,1]. Ранее было полученоf(x) = 0.
; E = [0,1]. Ранее было полученоf(x) = 0.
Покажем, что сходимость {fn(x)} к f(x) не является равномерной.
Графики функций fn(x)= ![]() представляют собой семейство, получаемое сжатием к началу координат графика нечетной функции y =
представляют собой семейство, получаемое сжатием к началу координат графика нечетной функции y = ![]() , где t = nx.
, где t = nx.
Рассмотрим поведения экстремумов и точек перегиба.
yʹ = (fn(x)) ʹ = ![]() =
= ![]() ; yʹ = 0 приx = ±
; yʹ = 0 приx = ± ![]() , x =
, x = ![]() ,
,
y(![]() =
=  = 1,yʹʹ = (fn(x) ) ʹʹ =
= 1,yʹʹ = (fn(x) ) ʹʹ = ![]() ,
,
yʹʹ = 0 приx= 0, x = ± ![]() , f(
, f(![]() ) =
) =  =
= ![]()
Таким образом, на отрезке [0,1] имеем для всех функций семейства одинаковой высоты максимум ymax(![]() )=
)= ![]() и одинаковой высоты перегиб y =
и одинаковой высоты перегиб y = ![]() , но достигаются эти значения в разных точках для разных кривых: xmax =
, но достигаются эти значения в разных точках для разных кривых: xmax = ![]() , xперегиба
, xперегиба![]() .
.
На Рисунке 2.3 представлены графики f1(x),…,f6(x). На любом срезе x = x0 получаем числовую последовательность {fn(x0)}. Например, при x0 = 0,25
{fn(0,25)} = ![]() .
.
Последовательность {fn(![]() )} до n = 4 возрастает, а далее убывает и сходится к нулю.
)} до n = 4 возрастает, а далее убывает и сходится к нулю.
Для любого ε> 0 и любого фиксированного x0 неравенство
|fn(x0)![]() f(x0)| = |
f(x0)| = |![]() 0| < ε c учетом того, что
0| < ε c учетом того, что ![]() <
< ![]() =
= ![]() , заведомо выполнено, если
, заведомо выполнено, если ![]() < ε, то есть при n >
< ε, то есть при n > ![]() , N = N(
, N = N(![]() = [
= [![]() . В частности, при
. В частности, при ![]() =0,25,
=0,25, ![]() получим N(0,1;0,25)=[
получим N(0,1;0,25)=[![]() =81, |f81(0,25)
=81, |f81(0,25)![]() f(0,25)| = 0,0985 < 0,1
f(0,25)| = 0,0985 < 0,1
Однако, какого бы ни было N(ε,x0), всегда существует точка xmax = ![]() ,где n>N(ε,x0) и в этой точке |fn(
,где n>N(ε,x0) и в этой точке |fn(![]() )
)![]() f(
f(![]() )| = 1>ε (для любого ε<1).
)| = 1>ε (для любого ε<1).
Например, пусть ε = 0,1, x0 = 0,25, N = 81.Берем теперь x0 = 0,01. При
n = 100>81 имеем |f100(![]() )
)![]() f(
f(![]() )| = |1
)| = |1![]() 0| = 1 >ε.
0| = 1 >ε.
Таким образом, невозможнодля всех x, принадлежащих отрезку [0,1], при n>N(ε) обеспечить выполнение неравенства |fn(x)![]() f(x)|<ε. Последовательность сходится неравномерно.
f(x)|<ε. Последовательность сходится неравномерно.
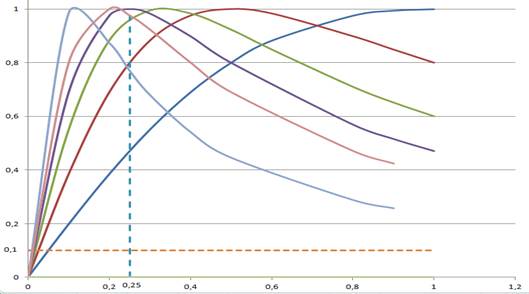
Рисунок 2.3. Пример неравномерной сходимости последовательности {![]() }
}
fn(х) = ![]() , E =[0,1].Ранее было получено f(х) = 0.
, E =[0,1].Ранее было получено f(х) = 0.
Рассмотрим функцию y = ![]() Так как, yʹ =
Так как, yʹ = ![]() , yʹ = 0 при х =
, yʹ = 0 при х = ![]() , x=
, x= ![]() ,y(
,y(![]() =
= 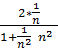 =
= ![]() , то функция имеет экстремум при х =
, то функция имеет экстремум при х = ![]() на [0,1] и этот экстремум равен y(
на [0,1] и этот экстремум равен y(![]() .
.
Далее yʹʹ = ![]() , yʹʹ = 0, x = ±
, yʹʹ = 0, x = ± ![]() , x =
, x = ![]() , y(
, y(![]() .
.
Таким образом, графики функций fn(х) = ![]() имеют на отрезке [0,1] максимумы, расположенные на прямой y = x и перегибы, расположенные на прямой y =
имеют на отрезке [0,1] максимумы, расположенные на прямой y = x и перегибы, расположенные на прямой y = ![]() . Так как fn(х) =
. Так как fn(х) = ![]() =
= ![]() , то графики функций fn(х) получаются из соответствующих графиков примера 3 сжатием в n раз вдоль оси ординат. При
, то графики функций fn(х) получаются из соответствующих графиков примера 3 сжатием в n раз вдоль оси ординат. При ![]() максимумы все ниже и график выравнивается, сглаживаясь к оси 0х. Это изменяет качество сходимости последовательности {fn(x)} и появляется возможность одновременного приближения графиков функций с ростом n к графику предельной функции f(x) = 0 на всем отрезке [0,1].
максимумы все ниже и график выравнивается, сглаживаясь к оси 0х. Это изменяет качество сходимости последовательности {fn(x)} и появляется возможность одновременного приближения графиков функций с ростом n к графику предельной функции f(x) = 0 на всем отрезке [0,1].
На Рисунке 2.4 показана динамика изменения графиков (сравнить с Рисунком 2.3). Возможность выбора единого N(ε) следует из оценки: |fn(x)![]() f(x)|<|fmax
f(x)|<|fmax![]() f(x)| =
f(x)| = ![]() <ε, n>
<ε, n>![]() .
.
Таким образом, ∀![]() существует N(ε) = [
существует N(ε) = [![]() +1, следовательно, сходимость равномерная.
+1, следовательно, сходимость равномерная.

Рисунок 2.4. Пример равномерной сходимости последовательности {![]() }
}
Пример 6.
Пусть fn(x) = ![]() +
+ ![]() , где D(x) – функция Дирихле.
, где D(x) – функция Дирихле.
D(x) = ![]() ;
;
Исследовать на равномерную сходимость на E = [0,1].
Решение.
fn(x) = 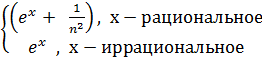
Каждая из функций fn(x) разрывна во всех точках E = [0,1].
f(x) = ![]() fn(x) =
fn(x) = ![]() , ∀
, ∀![]() .
.
Так как, |fn(x)![]() f(x)| =
f(x)| =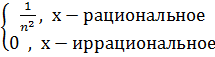 , |fn(x)-f(x)| =
, |fn(x)-f(x)| = ![]() <ε, n2>
<ε, n2>![]() , N(ε) = [
, N(ε) = [![]() +1, следовательно, ∀ε>0 существует N(ε), пригодное ∀
+1, следовательно, ∀ε>0 существует N(ε), пригодное ∀![]() и удовлетворяющее определению равномерной сходимости.
и удовлетворяющее определению равномерной сходимости.
Таким образом, сходимость последовательности разрывных функций {fn(x)} к непрерывной функции f(x) = ![]() является равномерной.
является равномерной.
Пример 7 [3].
fn(x) =  , E = [0,1]
, E = [0,1]
Исследовать на равномерную сходимость.
Решение.
Функции fn(x) всюду разрывные. f(x) = ![]() fn(x) =
fn(x) = ![]() ,
,
|fn(x)![]() f(x)| =
f(x)| = 
Неравенство |fn(x)![]() f(x)| <ε выполняется при
f(x)| <ε выполняется при ![]() <ε, n>
<ε, n>![]() .
.
Таким образом, ∀ε>0 существует N(ε) = [![]() +1, удовлетворяющее определению равномерной сходимости.
+1, удовлетворяющее определению равномерной сходимости.
Итого, сходимость последовательности всюду разрывных функций {fn(x)} к непрерывной функции f(x) = 0 является равномерной.
Пример 8.
fn(x) = 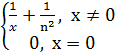
Исследовать на равномерную сходимость на отрезке [0,1].
Решение.
Функции fn(x) неограниченны на [0,1], при x =0 имеют разрыв второго рода. Для ∀x![]() имеем f(x) =
имеем f(x) = ![]() fn(x) =
fn(x) = ![]() . Для x = 0 имеем
. Для x = 0 имеем
fn(0) = 0 и![]() fn(0) =0.
fn(0) =0.
Таким образом, f(x) = 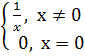 . Функция f(x) разрывна при x =0.
. Функция f(x) разрывна при x =0.
|fn(x)![]() f(x)|=
f(x)|= 
Для выполнения неравенства |fn(x)![]() f(x)|<ε необходимо, чтобы
f(x)|<ε необходимо, чтобы ![]() <ε. То есть n>
<ε. То есть n>![]() .
.
Положим N(ε) = [![]() +1. Таким образом, существует N(ε), пригодное ∀
+1. Таким образом, существует N(ε), пригодное ∀![]() и удовлетворяющее определению равномерной сходимости.
и удовлетворяющее определению равномерной сходимости.
Итого, наша последовательность разрывных функций сходится равномерно к разрывной функции.
Разобранные примеры дают возможность проанализировать, как влияет качество сходимости (равномерная или нет) на результат предельного перехода:
· пример 1 и 2 — последовательность непрерывных функций поточечно сходится к разрывной функции;
· пример 3 — последовательность непрерывных функций поточечно сходится к непрерывной функции;
· пример 4 — последовательность непрерывных функций равномерно сходится к непрерывной функции;
· пример 6 — последовательность разрывных функций равномерно сходится к непрерывной функции;
· пример 7 — последовательность разрывных функций сходится равномерно к непрерывной функции;
· пример 8 — последовательность разрывных функций равномерно сходится к разрывной функции;
· пример 5 — последовательность непрерывных функций неравномерно сходится к непрерывной функции (доказано далее в примере 9).
Справедлива следующая теорема о непрерывности предела последовательности [1].
Теорема 1 :
Если все члены последовательности непрерывны в точке х0![]() Е и последовательность сходится равномерно на Е, то предельная функция непрерывна в точке х0.
Е и последовательность сходится равномерно на Е, то предельная функция непрерывна в точке х0.
Из этой теоремы следует, что невозможно построить пример последовательности непрерывных функций, сходящихся равномерно к разрывной функции.
При исследовании последовательности на равномерную сходимость удобно пользоваться вышеупомянутой перефразировкой определения равномерной сходимости. Последовательность {fn(x)} равномерно сходится к f(x) тогда и только тогда, когда ![]() |fn(x)
|fn(x)![]() f(x)|= 0. Например, пусть fn(х) =
f(x)|= 0. Например, пусть fn(х) = ![]() , E =[0,1]. Ранее в примере 4 было получено f(х) = 0 и
, E =[0,1]. Ранее в примере 4 было получено f(х) = 0 и ![]() fn(х) =
fn(х) = ![]() , значит
, значит ![]() |fn(x)
|fn(x)![]() f(x)|=
f(x)|= ![]() =
=![]() =0. Сходимость равномерная.
=0. Сходимость равномерная.
Пример 9.
fn(x) ![]() , E = [0,1]. Исследовать на равномерную сходимость.
, E = [0,1]. Исследовать на равномерную сходимость.
Решение.
Ранее в примере 5 было получено, что f(x) = 0 на отрезке [0,1], поточечная сходимость есть.
Найдем максимум функции y = fn(x).
yʹ =![]() =
= ![]() , yʹ =0, x = ±
, yʹ =0, x = ± ![]() , x =
, x = ![]() [0,1],
[0,1],
y(![]() =
= ![]() =
=![]() .Итого, fn(x) ≤
.Итого, fn(x) ≤ ![]() , f(x) = 0.
, f(x) = 0.
![]() |fn(x)
|fn(x)![]() f(x)| =
f(x)| =![]() (
(![]() =
= ![]() ≠0. Равномерной сходимости нет.
≠0. Равномерной сходимости нет.
В примере 9 последовательность {fn(x)} непрерывных функций сходится неравномерно к непрерывной функции.
Рассмотрим далее, как связаны понятия равномерной сходимости с операциями дифференцирования и интегрирования. Справедливы следующие теоремы [1].
Теорема 2: если все члены последовательности {fn(x)} интегрируемы на [a, b] и последовательность {fn(x)} сходится равномерно на [a, b], то функция f(x)=![]() fn(x) интегрируема на [a,b] для любого x0 ∈[a,b] и
fn(x) интегрируема на [a,b] для любого x0 ∈[a,b] и ![]() на[a, b] .
на[a, b] .
Теорема 3: если функции fn(x) дифференцируемы на [a,b], последовательность {fnʹ(x)} сходится равномерно на [a, b] и последовательность {fn(x)} сходится хотя бы в одной точке x0 ∈[a, b], то последовательность {fn(x)} сходится равномерно на [a, b] к дифференцируемой функции и
(![]() fn(x)) ʹ =
fn(x)) ʹ = ![]() fnʹ(x) для ∀x ∈ [a, b].
fnʹ(x) для ∀x ∈ [a, b].
Отметим, что теоремы 1, 2, 3 о непрерывности, интегрируемости и дифференцируемости предела последовательности дают только достаточные условия того, что предельная функция обладает соответствующими свойствами.
Пример 10.
fn(x) = ![]() , E = [0,1]. Проверить возможность предельного перехода под знаком интеграла.
, E = [0,1]. Проверить возможность предельного перехода под знаком интеграла.
Решение.
Ранее в примере 3 найдено f(x) = 0 и сходимость неравномерная. Вычислим предел интеграла от ![]() .
.
![]() =
=![]() =
=![]() =
=
![]() ) =
) =![]() =
= ![]() =
= ![]() =0
=0
Далее
![]() =
=![]() =
=![]() = 0
= 0
Таким образом, несмотря на то, что сходимость не является равномерной, имеем ![]() =
= ![]() , а значит предельный переход под знаком интеграла возможен.
, а значит предельный переход под знаком интеграла возможен.
Пример 11 [3].
![]() . E = [0,1]. Проверить возможность предельного перехода под знаком интеграла.
. E = [0,1]. Проверить возможность предельного перехода под знаком интеграла.
Решение.
![]() =
= ![]() =
= ![]() =
=
= (-![]() +1),
+1),
![]() =
= ![]() (-
(-![]() +1) = 1
+1) = 1
Далее найдем предельную функцию.
f(x) = ![]() =
= ![]() =
= ![]() =
= ![]() = 0 ∀x∈ (0,1]. Так как
= 0 ∀x∈ (0,1]. Так как ![]() = 0, то f(x) = 0 ∀x∈ [0,1]. Вычислим интеграл от предельной функции.
= 0, то f(x) = 0 ∀x∈ [0,1]. Вычислим интеграл от предельной функции.
![]() dx =
dx = ![]() dx = 0.
dx = 0.
Таким образом, ![]() ≠
≠![]() , то есть предельный переход под знаком интеграла невозможен.
, то есть предельный переход под знаком интеграла невозможен.
Пример 12 [2].
![]() = n2x
= n2x![]() . E = [0,1].Проверить возможность предельного перехода под знаком интеграла.
. E = [0,1].Проверить возможность предельного перехода под знаком интеграла.
Решение.
Найдем предельную функцию.
Для любого x∈ (0,1] имеем
f(x) = ![]() =
=![]() =
= ![]() =
= ![]() =
= ![]() =0
=0
Для x=0 имеем ![]() ,
, ![]() = 0. Таким образом, f(x) = 0∀x∈ [0,1].
= 0. Таким образом, f(x) = 0∀x∈ [0,1].
![]() dx = 0.
dx = 0.
Далее интегрируем по частям.
![]() =
= ![]() = n2[(-
= n2[(-![]() +
+ ![]() ] = n2[ -
] = n2[ - ![]() -
- ![]() ] =
] =
|
x = U |
dU = dx |
|
|
V = |
![]() + 1
+ 1
![]() =
= ![]() (
(![]() + 1) = 1.
+ 1) = 1.
Таким образом, ![]() ≠
≠![]() , а, следовательно, предельный переход под знаком интеграла невозможен.
, а, следовательно, предельный переход под знаком интеграла невозможен.
Отметим, что из полученного результата по теореме 2 дополнительно следует, что сходимость {fn(x)} = {n2x![]() не является равномерной.
не является равномерной.
Примеры 10-12 демонстрируют, что условие равномерной сходимости интегрируемых функций на [a,b] существенно, но не является необходимым для возможности предельного перехода под знаком интеграла.
Пример 13.
![]() , E =[0,1]. Проверить будет ли справедливо равенство
, E =[0,1]. Проверить будет ли справедливо равенство ![]() =
=![]()
Решение.
Ранее в примере 4 показано, что последовательность непрерывных функций {fn(x)} равномерно сходится к непрерывной функции f(x)= 0. Находим производную от предельной функции на [0,1]. ![]() = (f(x))
= (f(x))![]() = 0
= 0![]()
Далее найдем последовательность из производных.
![]() =
=![]() =
= ![]() =
= ![]() .
.
Пусть x![]() , тогда
, тогда![]() =
= ![]() =
=  =
= 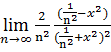 = 0.
= 0.
Если х = 0, то ![]() =
= ![]() = 2 ,
= 2 , ![]() 2 = 2.
2 = 2.
Итак, ![]() =
= ![]() . Таким образом,
. Таким образом, ![]() ≠
≠![]() .
.
Из полученного результата по теореме 3 следует, что последовательность {![]() не сходится равномерно на [0,1], так как в противном случае, все условия теоремы 3 выполнялись бы и нарушение последнего равенства было бы невозможно.
не сходится равномерно на [0,1], так как в противном случае, все условия теоремы 3 выполнялись бы и нарушение последнего равенства было бы невозможно.
Из определения равномерной сходимости следует, что, если последовательности {![]() и
и ![]() сходятся равномерно на E, то последовательность {α
сходятся равномерно на E, то последовательность {α![]() сходится равномерно на E. В частности, если
сходится равномерно на E. В частности, если ![]() — числовая сходящаяся последовательность, то {
— числовая сходящаяся последовательность, то {![]() — равномерно сходится на E. Если {
— равномерно сходится на E. Если {![]() сходится неравномерно, то
сходится неравномерно, то
{![]() сходится неравномерно.
сходится неравномерно.
Отметим также, что заменой переменной t = a+(b![]() a)x отрезок [0,1] можно преобразовать в отрезок [a,b].
a)x отрезок [0,1] можно преобразовать в отрезок [a,b].
Например, для последовательности {![]() , где
, где ![]() и E =[0,1] получим на отрезке [3,5] после замены t=3 +2x новую функциональную последовательность непрерывных функций {
и E =[0,1] получим на отрезке [3,5] после замены t=3 +2x новую функциональную последовательность непрерывных функций {![]() , где
, где ![]() , равномерно сходящуюся на [3,5] к предельной функции f(x) = 0.
, равномерно сходящуюся на [3,5] к предельной функции f(x) = 0.
Последовательность {![]() = {
= {![]() +
+ ![]() } сходится равномерно на [3,5] к функции (
} сходится равномерно на [3,5] к функции (![]() .
.
3. Равномерная сходимость функциональных рядов
Напомним, что ряд вида ![]() где
где ![]() — функции, определенные на общей области D, называются функциональным рядом.
— функции, определенные на общей области D, называются функциональным рядом.
Совокупность всех точек сходимости функционального ряда ![]() называется множеством сходимости.
называется множеством сходимости.
На множестве E сходимости ряда определена функция S(x) = ![]() ,S(x) — сумма ряда.
,S(x) — сумма ряда.
S(x) = ![]() , где{Sn(x)} — последовательность частичных сумм.
, где{Sn(x)} — последовательность частичных сумм.
Ряд ![]() называется равномерно сходящимся на множествеЕ, если последовательность {Sn(x)} его частичных сумм равномерно сходится на Е, то есть
называется равномерно сходящимся на множествеЕ, если последовательность {Sn(x)} его частичных сумм равномерно сходится на Е, то есть
![]() Sn(x)
Sn(x) ![]() S(x)| <
S(x)| <![]() .
.
Если обозначить rn(x) –n-ый остаток ряда,
rn(x) = S(x) ![]() Sn(x) =
Sn(x) = ![]() ,
,
то из определения следует, что ![]() <
<![]() ,
, ![]() , а, следовательно, равномерная сходимость ряда на E эквивалентна равномерной сходимости к нулю последовательности остатков
, а, следовательно, равномерная сходимость ряда на E эквивалентна равномерной сходимости к нулю последовательности остатков ![]() , то есть
, то есть ![]() =0.
=0.
Пример 14.
![]() на E = (
на E = (![]() ,
, ![]() ). Исследовать на равномерную сходимость.
). Исследовать на равномерную сходимость.
Решение.
Обозначим q = ![]() 0 <q<
0 <q<![]() <1, следовательно
<1, следовательно![]() сходится как бесконечно убывающая геометрическая прогрессия и его сумма равна S=
сходится как бесконечно убывающая геометрическая прогрессия и его сумма равна S= ![]() ,
,
Sn= ![]() , rn =
, rn = ![]() <
<![]() (так как
(так как ![]() <
<![]() , 1
, 1 ![]() ,
,
![]() <
<![]() ,
,![]() <
<![]() ). Таким образом,
). Таким образом, ![]() . Так как
. Так как ![]() ≥ 0 на E, то
≥ 0 на E, то ![]() =0 и ряд сходится равномерно.
=0 и ряд сходится равномерно.
Пример 15.
![]() Исследовать ряд на равномерную сходимостьна отрезке [0,1].
Исследовать ряд на равномерную сходимостьна отрезке [0,1].
Решение.
Ряд знакочередующийся и удовлетворяет всем условиям признака Лейбница. Из признака Лейбница имеем оценку остаточного члена
![]() . Отсюда,
. Отсюда, ![]() имеем
имеем
|![]() | < |
| < |![]() | =
| = ![]() <
<![]() ,
, ![]() . Ряд сходится равномерно.
. Ряд сходится равномерно.
Для функциональных рядов справедлив необходимый признак равномерной сходимости [1].
Теорема 4 (необходимое условие равномерной сходимости):
Если ряд ![]() сходится равномерно на множестве E, то последовательность
сходится равномерно на множестве E, то последовательность ![]() сходится к нулю.
сходится к нулю.
Теорема 4 является необходимым условием равномерной сходимости, ноне является достаточным. Однако, нарушение равномерной сходимости последовательности ![]() к нулю влечет за собой отсутствие равномерной сходимости функционального ряда.
к нулю влечет за собой отсутствие равномерной сходимости функционального ряда.
Если {![]() } неравномерно сходится к нулю, то ряд может или сходиться неравномерно или расходиться. Если
} неравномерно сходится к нулю, то ряд может или сходиться неравномерно или расходиться. Если ![]() ≠ 0, то ряд расходится.
≠ 0, то ряд расходится.
Пример 16.
![]() , E = [0,1]. Проверить выполнимость необходимого условия равномерной сходимости.
, E = [0,1]. Проверить выполнимость необходимого условия равномерной сходимости.
Решение.
Обозначим ![]() = {
= {![]() . Исследуем эту последовательность на равномерную сходимость. Найдем предельную функцию U(x):
. Исследуем эту последовательность на равномерную сходимость. Найдем предельную функцию U(x):
![]() ,
, ![]() U(x) = 0.
U(x) = 0.
Так как ![]() =
=![]() =
= ![]() то последовательность
то последовательность ![]() равномерно сходится к нулю.
равномерно сходится к нулю.
Покажем, что ряд ![]() расходится. Так как
расходится. Так как ![]() < n,
< n, ![]() >
> ![]() и гармонический ряд
и гармонический ряд ![]() расходится, то ряд
расходится, то ряд ![]() расходится (по теореме сравнения). Для любого x0
расходится (по теореме сравнения). Для любого x0![]() ряды
ряды ![]() и
и ![]() удовлетворяют предельной теореме сравнения, следовательно ряд
удовлетворяют предельной теореме сравнения, следовательно ряд ![]() расходится, несмотря на то, что последовательность
расходится, несмотря на то, что последовательность ![]() равномерно сходится к нулю.
равномерно сходится к нулю.
При исследовании функционального ряда удобно использовать достаточный признак Вейерштрасса.
Теорема 5 (признак Вейерштрасса) [1]:
Если для функционального ряда ![]() существует сходящийся положительный числовой ряд
существует сходящийся положительный числовой ряд ![]() такой, что |
такой, что |![]() | ≤
| ≤![]() то
то ![]() сходится абсолютно и равномерно на E.
сходится абсолютно и равномерно на E.
Ряд ![]() называется мажорантным. Оптимальным мажорантным рядом при использовании признака Вейерштрасса является ряд
называется мажорантным. Оптимальным мажорантным рядом при использовании признака Вейерштрасса является ряд ![]() На практике достаточно бывает и более грубой оценки.
На практике достаточно бывает и более грубой оценки.
Пример 17.
![]() , E = [0;2]. Исследовать на равномерную сходимость.
, E = [0;2]. Исследовать на равномерную сходимость.
Решение.
![]() | = |
| = |![]() | <
| <![]()
Рассмотрим ряд ![]() . Так как ряд Дирихле
. Так как ряд Дирихле ![]() сходится (p =
сходится (p = ![]() > 1), то ряд
> 1), то ряд ![]() сходится. По признаку Вейерштрасса ряд
сходится. По признаку Вейерштрасса ряд ![]() сходится равномерно и абсолютно.
сходится равномерно и абсолютно.
Пример 18 [1].
![]() , E = [0;1]. Исследовать ряд на равномерную сходимость.
, E = [0;1]. Исследовать ряд на равномерную сходимость.
Решение.
![]() =2
=2![]() =
= ![]()
![]() =0 при x=0 и x =
=0 при x=0 и x = ![]() . Так как
. Так как ![]() = 0 и
= 0 и ![]() (
(![]() =
= ![]() , то
, то![]() <
<![]() .
.
Рассмотрим мажорантный ряд:
![]() ̶ сходится; p=2 > 1 (ряд Дирихле).
̶ сходится; p=2 > 1 (ряд Дирихле).
По признаку Вейерштрасса ряд ![]() сходится равномерно.
сходится равномерно.
Пример 19.
![]() , E = [
, E = [![]() . Доказать равномерную сходимость на E
. Доказать равномерную сходимость на E![]()
Чтобы сделать оценку общего члена рассмотрим функцию ![]() на [
на [![]()
Первое слагаемое самое большое значение имеет в точке x =2 и равно ![]() , второе слагаемое самое большое в точке x=
, второе слагаемое самое большое в точке x= ![]() и равно 5*
и равно 5*![]() Значит сумма на всем отрезке [
Значит сумма на всем отрезке [![]() не более, чем сумма самых больших возможностей.
не более, чем сумма самых больших возможностей.
![]() <
<![]() Следовательно,
Следовательно,
![]() =
= ![]() (
(![]() .
.
Ряд ![]() сходится по признаку Даламбера так как
сходится по признаку Даламбера так как ![]() =
=![]() = 0 < 1. Следовательно,
= 0 < 1. Следовательно, ![]() сходится равномерно по признаку Вейерштрасса.
сходится равномерно по признаку Вейерштрасса.
Следующий пример показывает, что признак Вейерштрасса является достаточным для равномерной и абсолютной сходимости, но не является необходимым.
Пример 20.
![]() , E= [0,1]. Исследовать на равномерную и абсолютную сходимость.
, E= [0,1]. Исследовать на равномерную и абсолютную сходимость.
Решение.
Данный ряд является знакопеременным. Исследуем его на абсолютную сходимость. Так как ![]() =
=![]() ,
,![]() (при n
(при n![]() и ряд Дирихле
и ряд Дирихле ![]() расходится (p=
расходится (p=![]() < 1), то ряд
< 1), то ряд ![]() расходится
расходится ![]() , а следовательно, ряд
, а следовательно, ряд ![]() не сходится абсолютно. Исходный ряд является знакочередующимся и удовлетворяет всем условиям признака Лейбница, а значит данный ряд сходится условно. Оценка остаточного члена по признаку Лейбница дает |rn(x)| <
не сходится абсолютно. Исходный ряд является знакочередующимся и удовлетворяет всем условиям признака Лейбница, а значит данный ряд сходится условно. Оценка остаточного члена по признаку Лейбница дает |rn(x)| <![]() <
<![]() ,
, ![]() |rn(x)| <
|rn(x)| <![]() = 0.
= 0.
Таким образом,![]() rn(x) = 0 и исходный ряд
rn(x) = 0 и исходный ряд ![]() сходится равномерно, хотя и не сходится абсолютно, а лишь условно.
сходится равномерно, хотя и не сходится абсолютно, а лишь условно.
Покажем дополнительно, что необходимый признак равномерной сходимости выполнен.
Найдем предельную функцию последовательности {Un(x)}. Так как
U(x) =![]() =0, U(x) = 0 и
=0, U(x) = 0 и ![]() =
= ![]() ,
,
![]() |Un(x)–U(x)|=
|Un(x)–U(x)|=![]() |
|![]() |=
|=![]() =0. Таким образом последовательность
=0. Таким образом последовательность ![]() сходится к нулю равномерно.
сходится к нулю равномерно.
Этот пример также показывает, что необходимый признак равномерной сходимости не является достаточным.
Отметим, что из соотношения ![]() (x)при
(x)при ![]() , вообще говоря, не следует, что ряды
, вообще говоря, не следует, что ряды ![]() одновременно равномерно сходятся или одновременно неравномерно сходятся. Приведем пример, демонстрирующий это замечание.
одновременно равномерно сходятся или одновременно неравномерно сходятся. Приведем пример, демонстрирующий это замечание.
Пример 21 [1].
![]() и
и ![]() ,E = (
,E = (![]() . Исследовать ряды на равномерную сходимость.
. Исследовать ряды на равномерную сходимость.
Решение.
Заметим, что ![]() при n
при n![]() . Исследуем данные ряды на сходимость.
. Исследуем данные ряды на сходимость.
1) ![]() =
= ![]() ,
,
Так как (|x| – n)2 > 0; x2 +n2>![]() ,
, ![]() <
<![]() ;
; ![]() <
<![]() то
то
| ![]() | <
| <![]() . Итого: |
. Итого: |![]() | <
| <![]() .
.
Так как мажорантный ряд![]() сходится, то по признаку Вейерштрасса ряд
сходится, то по признаку Вейерштрасса ряд ![]() сходится равномерно.
сходится равномерно.
2) ![]() =
=![]() . Исследуем на абсолютную сходимость.
. Исследуем на абсолютную сходимость.
![]() = |x|
= |x| ![]() сходится как ряд Дирихле (p = 3>1). Таким образом, ряд
сходится как ряд Дирихле (p = 3>1). Таким образом, ряд ![]() сходится абсолютно.
сходится абсолютно.
Рассмотрим последовательность ![]() ={
={![]() }. Покажем, что последовательность {
}. Покажем, что последовательность {![]() не сходится равномерно. Найдем предельную функцию V(x).
не сходится равномерно. Найдем предельную функцию V(x).
V(x) =![]() =
= ![]() = 0,
= 0, ![]() |
|![]() V(x) | =
V(x) | = ![]() =
= ![]() =
= ![]() , E = (
, E = (![]() , следовательно, последовательность {
, следовательно, последовательность {![]() не сходится равномерно к нулю .
не сходится равномерно к нулю .
Ряд ![]() не сходится на E равномерно, так как не выполнено необходимое условие равномерной сходимости (см. теорему 4).
не сходится на E равномерно, так как не выполнено необходимое условие равномерной сходимости (см. теорему 4).
Ряд ![]() сходится на E неравномерно.
сходится на E неравномерно.
Таким образом получили ![]() (x) (
(x) (![]() , ряд
, ряд ![]() сходится равномерно, а ряд
сходится равномерно, а ряд ![]() сходится неравномерно.
сходится неравномерно.
Из разобранных нами примеров следует, что абсолютно сходящийся ряд может быть как равномерно сходящимся (пример 17; пример 21, п. 1), так и неравномерно (пример 21, п. 2). Условно сходящийся ряд также может быть равномерно сходящимся (пример 20).
Примеры рядов, сходящихся равномерно/неравномерно с соответствующими функциональными свойствами суммы ряда (непрерывность, интегрируемость, дифференцируемость) можно построить, например, используя рассмотренные функциональные последовательности ![]() , если положить Sn(x) = fn(x). Тогда U1(x) = f1(x),Un(x) = fn(x)
, если положить Sn(x) = fn(x). Тогда U1(x) = f1(x),Un(x) = fn(x) ![]() fn-1(x) (n=2;3…). Получим ряд
fn-1(x) (n=2;3…). Получим ряд ![]() =f1(x) +
=f1(x) +![]() ).
).
Например, если ![]() = {2xn2
= {2xn2![]() }, то ряд
}, то ряд ![]() сходится на [0,1] неравномерно к непрерывной сумме S=0 [3].
сходится на [0,1] неравномерно к непрерывной сумме S=0 [3].
Отметим, что степенной ряд равномерно сходится на всяком отрезке, целиком лежащем внутри интервала сходимости, имеет непрерывную суммуS(x) в интервале сходимости, его можно почленно дифференцировать и полученный ряд сходится в том же интервале к S![]() (x). Степенной ряд можно почленно интегрировать внутри интервала сходимости и полученный ряд сходится к интегралу от S(x) [3].
(x). Степенной ряд можно почленно интегрировать внутри интервала сходимости и полученный ряд сходится к интегралу от S(x) [3].
Список литературы:
1.Виноградова И.А., Олехник С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу, Ч2, М.: Дрофа, 2001.
2.Гелбаум Б., Олмстед Дж., Контрпримеры в анализе, М.: Мир, 1967.
3.Фихтенгольц Г.М. Курс дифференциального интегрального исчисления, т. I, М., 1960.
дипломов


Оставить комментарий