ПОСТРОЕНИЕ  ФУНКЦИЙ  НА  ПЛОСКОСТИ,  ЗАДАННЫХ  ПАРАМЕТРИЧЕСКИ

Билялова  Виктория  Мухамедовна

студент,  Волжский  политехнический  институт  (филиал)  ФГБОУ  ВПО  «Волгоградский  государственный  технический  университет»,  РФ,  г.  Волгоград

Е -mail: 

Матвеева  Татьяна  Александровна

доцент,  канд.  физ.-мат.  наук,  Волжский  политехнический  институт  (филиал)  ФГБОУ  ВПО  «Волгоградский  государственный  технический  университет»,  РФ,  г.  Волгоград

Е-mail: 

Агишева  Джамиля  Калимулловна

старший  преподаватель,  Волжский  политехнический  институт  (филиал)  ФГБОУ  ВПО  «Волгоградский  государственный  технический  университет»,  РФ,  г.  Волгоград

CREATION  OF  FUNCTIONS  ON  THE  PLANE,  SET  PARAMETRICALLY

Bilyalova  Viktoriya

student,  Volzhsky  Politechnical  Institute  (branch)  Volgograd  Technical  University,  Russia,  Volgograd

Matveeva  Tatyana

associate  professor,  candidate  of  physics  and  mathematics,  Volzhsky  Politechnical  Institute  (branch)  Volgograd  Technical  University,  Russia,  Volgograd

Agisheva  Dzhamilya

senior  teacher,  Volzhsky  Politechnical  Institute  (branch)  Volgograd  Technical  University,  Russia,  Volgograd

АННОТАЦИЯ

В  настоящее  время  существование  большого  числа  математических  пакетов  явно  упрощают  жизнь  человека:  построение  графиков  и  вычисление  расчетов  делаются  компьютером  автоматически.  Однако  математические  пакеты  не  дают  полного  истолкования  своих  действий.  Так,  мы  видим  просто  построенный  график.  Но  что  же  скрывается  за  ним?  Почему  он  выглядит  именно  так?  Ответы  на  эти  вопросы  даёт  знание  дифференциального  исчисления.  В  статье  рассматривается  исследование  и  построение  функций  на  плоскости,  заданных  параметрически. 

ABSTRACT

Now  existence  of  a  large  number  of  mathematical  packages  obviously  simplify  human  life:  computer  performs  plotting  and  implementation  of  calculations  automatically.  However,  mathematical  packages  don't  give  full  interpretation  of  the  actions.  So,  we  see  simply  constructed  graph.  But  what  is  behind  it?  Why  does  it  look  quite  so?  Answers  to  these  questions  are  given  by  knowledge  of  differential  calculus.  In  the  article  research  and  creation  of  the  functions  on  the  plane  set  parametrically  are  considered.

Ключевые  слова:   параметрические  функция;  дифференциальное  исчисление.

Keywords:   parametrical  function;  differential  calculus.

Довольно  часто  мы  сталкиваемся  с  тем,  что  привычные  для  нас  кривые  не  считаются  графиками  функций  заданных  уравнением  ,  так  как  в  декартовой  системе  координат  некоторым  абсциссам  соответствуют  несколько  ординат  этой  кривой.  Так,  например,  обычная  окружность  не  является  графиком  функции.  С  точки  зрения  графического  представления  у  явного  задания  функции  имеются  весьма  существенные  недостатки:  каждому  значению  х  соответствует  только  одно  значение  у;  кривая  не  может  быть  замкнутой.  В  результате  явный  способ  представления  функции  нельзя  применять  там,  где  требуется  описание  произвольных  кривых,  которые  размещаются  в  произвольных  местах  на  плоскости. 

Альтернативным  способом  является  определение  кривой  как  параметрической  функции.  У  этого  способа  задания  кривой  обе  координаты    имеют  равные  права.  Такая  зависимость  в  общем  случае  получает  вид  ,  где    и    —  функции  параметра  t. 

Сегодня,  для  решения  инженерных  задач,  построения  графиков,  проведения  математических  экспериментов  и  т.п.  существует  большое  множество  математических  пакетов,  таких  как  Mathcad,  Mathematica,  Maple.  Система  Mathcad  —  это  одна  из  популярных  систем  компьютерной  математики,  которая  предназначена  для  автоматизации  решения  математических  задач  в  массовом  применении  в  различных  областях  техники,  науки  и  образования.  Выбор  системы  Mathcad,  обусловлен  ее  распространенностью  и  возможностью  описать  математические  алгоритмы  в  естественной  математической  форме  с  применением  общепринятой  символики  для  математических  знаков.

Однако  любой  математический  пакет  не  предусматривает  полного  анализа  графика,  а  только  предоставляет  построенный  график,  значения  функции  от  разных  переменных,  оставляя  скрытыми  от  нас  вычисления  асимптот,  точек  экстремума,  перегиба  и  т.п. 

Для  примера  построим  график  функции,  заданной  в  параметрическом  виде  в  среде  Mathcad  (Рис.  1).

Рисунок  1  График  параметрической  функции,  построенный  в  математическом  пакете  Mathcad

По  получившемуся  графику  функции  можно  предположить,  что  он  имеет  горизонтальную,  вертикальную  и  наклонную  асимптоты,  также  наблюдаем  точки  экстремума  и  точку  возврата,  но  каким  значения  параметра  t  это  соответствует  «скрыто». 

Рассмотрим  полное  исследование  функции  с  помощью  дифференциального  исчисления  и  построение  графика  функции  заданной  параметрически: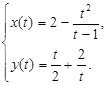 

Область  определения:  .

Найдем  асимптоты  данного  графика  функции.  Они  играют  важную  роль  при  анализе  и  построении  графиков.  Различают  вертикальные,  горизонтальные  и  наклонные  асимптоты. 

Вертикальные  асимптоты  определяются  точками  разрыва  функции  .  В  нашем  случае  функция    имеет  точку  разрыва  ,  также  она  является  точкой  поворота.  Тогда   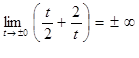 ,  т.  е.  получаем,  что    –  вертикальная  асимптота.

Горизонтальная  асимптота  в  свою  очередь  определяются  точками  разрыва  функции  .  Так  как    имеет  разрыв  в  точке  ,  то  получаем    .

Таким  образом,    является  горизонтальной  асимптотой.

Найдем  наклонную  асимптоту  вида  ,  где 

,

.

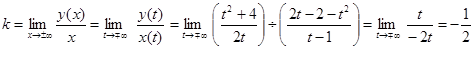Подставляя  полученные  значения    в  уравнение  наклонной  асимптоты,  имеем 

Найдем  точки  пересечения  графика  функции  с  осями  координат: 

а)  с  осью  Ox:    -  не  имеет  корней;

б)  с  осью  Oy:    не  имеет  корней.  Таким  образом,  график  функции  не  пересекает  оси  координат.

Вычислим  первую  производную,  определим  промежутки  монотонности  и  экстремумы  функции. 

  .

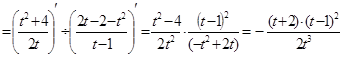При  имеем    –  точку  минимума.

При  имеем  –  вертикальную  асимптоту.

  Вычислим  вторую  производную,  определим  промежутки  выпуклости-вогнутости  графика  функции  и  точки  перегиба.

.

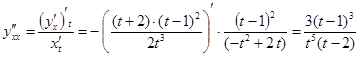При  имеем  при    имеем    точку  перегиба.

По  результатам  исследования,  заполним  таблицу  1.

Таблица  1. 

Сводная  таблица  исследования  графика  функции

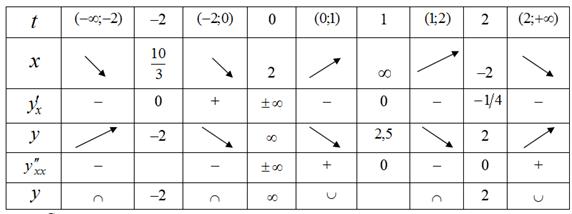
Сначала  строим  асимптоты,  наносим  точки  локальных  максимумов  и  минимумов  функции,  точки  перегиба  и  промежуточные  точки,  опираясь  на  сводную  таблицу  исследования  функции  (рис.  2).

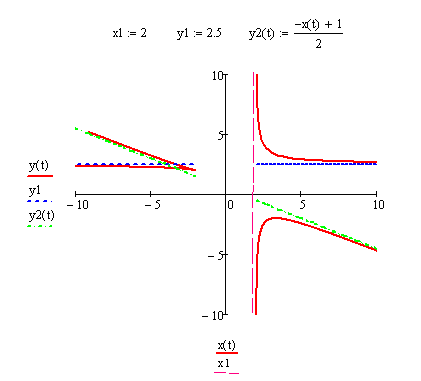
Рисунок  2.  График  функции

Таким  образом,  для  построения  графиков  параметрически  заданных  функций  необходимо  знание  дифференциального  исчисления.  Математические  пакеты  удобны  только  для  графической  визуализации,  но  не  подходят  при  поиске  значений  параметра  t  для  точек  экстремума,  перегиба  и  т.  п. 

Отметим  особенности  параметрических  кривых:  обе  координаты    вычисляются  как  функции  вспомогательного  параметра,  т.  е.  они  равноправны;  кривые  имеют  более  разнообразные  формы,  чем  это  позволяют  явные  уравнения;  параметрическое  представление  важно  для  пространственных  кривых;  применение  параметрических  функций  позволяет  применять  более  сложные  функции  при  аппроксимации  физических  процессов. 

Список  литературы:

1.Владимирский  Б.М.  Математика.  Общий  курс  /  Б.М.  Владимирский.  СПб:  Лань,  2006.  —  960  с.:  ил.

2.Письменный  Д.Т.  Конспект  лекций  по  высшей  математике:  полный  курс  6-е  изд.,  испр.  /  Д.Т.  Письменный.  М.:  Айрис-пресс,  2007.  —  608  с.

3.Матвеева  Т.А.  Математический  анализ  в  таблицах.  Часть  1  [Электронный  ресурс]:  учебное  пособие/Т.А.  Матвеева,  С.А.  Зотова,  Д.К.  Агишева,  В.Б.  Светличная  //Сборник  «Учебные  пособия».  Серия  «Технические  дисциплины».  Выпуск  1.  Волжский:  ВПИ  (филиал)  ВолгГТУ,  2013  г. 

4.Мустафина  Д.А.  Дифференциальное  исчисление  функции  одной  и  нескольких  переменных  с  приложениями:  учеб.  пособие  Д.А.  Мустафина,  И.В.  Ребро,  С.Ю.  Кузьмин,  Н.Н.  Короткова.  ВПИ  (филиал)  ВолгГТУ.  Волгоград,  2009.  —  118  с.