Статья опубликована в рамках: XXVII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 04 февраля 2015 г.)
Наука: Математика
Секция: Геометрия и топология
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ИНВОЛЮТИВНОЕ ПРЕОБРАЗОВАНИЕ ТРЕХСОСТАВНОГО РАСПРЕДЕЛЕНИЯ ПРОЕКТИВНОГО ПРОСТРАНСТВА
Попов Юрий Иванович
канд. ф-м. наук, профессор Балтийского федерального университета имени И. Канта, РФ, г. Калининград,
E -mail: AndreyBudylkin@rambler.ru
INVOLUTIVE CONVERSION THREEFOLD PROJECTIVE SPACE DISTRIBUTION
Popov Yuri
candidate of Science, professor of Baltic federal university of I.Kant, Russia, Kaliningrad
АННОТАЦИЯ
В данной работе доказано, что проективное преобразование ![]() :
:![]() структурных форм
структурных форм ![]() проективного пространства является иволютивным, то есть
проективного пространства является иволютивным, то есть ![]() =
= ![]() . Следуя работе [7] показано, что инволютивное преобразование
. Следуя работе [7] показано, что инволютивное преобразование ![]() переводит трехсоставное распределение
переводит трехсоставное распределение ![]() [4] в двойственный ему образ
[4] в двойственный ему образ ![]() , заданный относительно тангенциального репера
, заданный относительно тангенциального репера ![]() . Рассмотрены аналитические признаки двойственности
. Рассмотрены аналитические признаки двойственности ![]() и
и![]() — подрасслоений, ассоциированных с данным H-распределением, относительно преобразования
— подрасслоений, ассоциированных с данным H-распределением, относительно преобразования ![]() и дана их геометрическая интерпретация. Индексы принимают значения:
и дана их геометрическая интерпретация. Индексы принимают значения:
![]()
![]()
![]()
![]()
![]()
ABSTRACT
In this paper it is proved that a projective transformation ![]() :
:![]() structural forms
structural forms ![]() of projective space is ivolyutive —
of projective space is ivolyutive — ![]() =
= ![]() . The involutive transformation
. The involutive transformation ![]() transforms threefold distribution
transforms threefold distribution ![]() in its dual image
in its dual image ![]() specified with respect to the tangential frame
specified with respect to the tangential frame ![]() . Having considered the analytical features of dualty
. Having considered the analytical features of dualty ![]() and
and ![]() — subbundles associated with the H-distribution, the transformation
— subbundles associated with the H-distribution, the transformation ![]() and given their geometric interpretation. The indices take the values:
and given their geometric interpretation. The indices take the values:
![]()
![]()
![]()
![]()
![]()
Ключевые слова: распределения; инволютивное преобразование; двойственный образ.
Keywords: distribution; involutive transformation; dual image.
§ 1. Задание трехсоставного распределения
1. Тройку распределений, образованную соответственно распределениями r-плоскостей L (L-распределение), m-плоскостей М (М-распределение), гиперплоскостей Н (Н-распределение, r<m<n-1) проективного пространства Рn с отношением инцидентности Х ÎLÌMÌH их соответствующих элементов в каждом центре X назовем трехсоставным распределением проективного пространства Рn или H-распределением [4], при этом L-распределение назовем базисным распределением, а М-распределение и Н-распределение — оснащающими распределениями.
Обозначим через Фn-r-1![]() (Ф-плоскость) и
(Ф-плоскость) и![]() (E-плоскость) характеристики гиперплоскости, полученные при смещениях центра Х вдоль интегральных кривых соответственно L-распределения, М-распределения. Плоскость Ф(Х) пересекает плоскость М(Х)по s-мерной плоскости Ls(X):
(E-плоскость) характеристики гиперплоскости, полученные при смещениях центра Х вдоль интегральных кривых соответственно L-распределения, М-распределения. Плоскость Ф(Х) пересекает плоскость М(Х)по s-мерной плоскости Ls(X):
Ф(Х)ÇМ(Х) = Ls(Х), s = m-r.
Кроме того, введем в рассмотрение плоскость Y(X) = [L(X); E(X)].
Адаптируем подвижной репер![]() проективного пространства Pn с H-распределением следующим образом:
проективного пространства Pn с H-распределением следующим образом:
![]()
Выбранный таким образом репер R является репером 1-го порядка R1. Относительно репера R1 главные формы H-распределения имеют следующий вид:
![]() (a)
(a)
![]() (1)
(1)
![]()
где
![]() (2)
(2)
Геометрические объекты ![]() и
и ![]() являются соответственно фундаментальными объектами 1-го и 2-го порядка H-распре-деления. Компоненты фундаментального объекта Г2 удовлетворяют дифференциальным уравнениям
являются соответственно фундаментальными объектами 1-го и 2-го порядка H-распре-деления. Компоненты фундаментального объекта Г2 удовлетворяют дифференциальным уравнениям
![]() (а)
(а)
![]()
![]()
![]() (b)
(b)
![]() (3)
(3)
![]()
![]() (c)
(c)
![]()
![]()
Кроме того, компоненты фундаментального объекта Г2 связаны соотношениями:
![]()
![]() (4)
(4)
![]()
Таким образом, относительно репера R1трехсоставноеH-распределение задается уравнениями (1), (3) и соотношениями (2), (4).
§ 2. Инволютивность преобразования ![]() :
:![]()
Рассмотрим систему из (n+1)2форм Пфаффа ![]() :
:
![]()
![]() (a)
(a)
![]()
![]()
![]()
![]() (b)
(b)
![]() (I)
(I)
![]() (c)
(c)
![]()
![]()
![]()
Формы ![]() удовлетворяют структурным уравнениям проективного пространства и задают инфинитезимальные перемещения тангенциального репера
удовлетворяют структурным уравнениям проективного пространства и задают инфинитезимальные перемещения тангенциального репера![]() :
:
![]() (5)
(5)
где
![]()
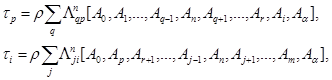 (6)
(6)
![]()
![]()
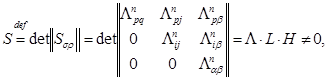
![]()
Докажем, что преобразование ![]() :
:![]() форм проективного пространства по закону (I) является инволютивным, т. е.
форм проективного пространства по закону (I) является инволютивным, т. е. ![]() =
= ![]() .
.
Прежде всего, из формул (1.а)
![]()
в силу соотношений (I.a) находим
![]() ; (7)
; (7)
![]()
![]() (8)
(8)
![]()
![]() (9)
(9)
Из формул ![]() и формул (7) получаем
и формул (7) получаем
![]() (10)
(10)
Дифференциальные уравнения (3.а), при K=q относительно тангенциального репера ![]() запишутся в виде
запишутся в виде
![]() (11)
(11)
Из уравнений (11), с использованием формул (I), (7), (3.а) находим
![]()
![]() (12)
(12)
![]()
![]()
Аналогично, из дифференциальных уравнений (3.b), при![]() и (3.с) при
и (3.с) при![]() , записанных относительно тангенциального репера (6), с учетом формул (1), (3.b), (3.с) соответственно получаем следующие соотношения:
, записанных относительно тангенциального репера (6), с учетом формул (1), (3.b), (3.с) соответственно получаем следующие соотношения:
![]()
![]() (13)
(13)
![]()
![]()
− − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
![]()
![]() (14)
(14)
![]()
![]()
Последние группы необходимых соотношений между объектами, отнесенными к различным реперам ![]() и
и ![]() , находим из соотношений
, находим из соотношений
![]()
с использованием формул (7)—(14):
![]()
![]() (15)
(15)
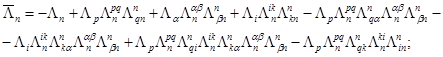
![]()
![]() (16)
(16)
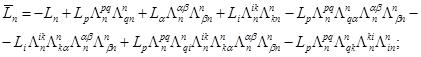
− − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
![]()
![]() (17)
(17)
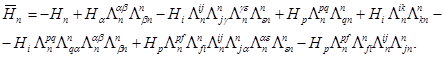
Наконец, разрешая формулы (I), с помощью соотношений (7)—(17), относительно ![]() , получаем формулы, определяющие преобразование
, получаем формулы, определяющие преобразование ![]()
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]() (II)
(II)
![]()
![]()
![]()
![]()
Теперь из (I) и (II) следует, что ![]() =
= ![]() . Дифференциальные уравнения регулярного -распределения, двойственного данному H-распределению, имеет вид, аналогичный уравнениям (1) (без соответствующих замыканий):
. Дифференциальные уравнения регулярного -распределения, двойственного данному H-распределению, имеет вид, аналогичный уравнениям (1) (без соответствующих замыканий):
![]()
![]() (18)
(18)
![]()
Таким образом справедлива
Теорема 1. Регулярное H-распределение проективного пространства Рn во второй дифференциальной окружности его образующего элемента индуцирует:
1. проективное пространство ![]() , двойственное исходному проективному пространству Рn относительно инволютивного преобразования
, двойственное исходному проективному пространству Рn относительно инволютивного преобразования ![]() форм
форм ![]() по закону (I),
по закону (I),
2. регулярное распределение ![]() , двойственное исходному, причем его дифференциальные уравнения в тангенциальном репере (5)-(6) имеют вид (18), аналогичный уровнениям (I) H-распределения проективного пространства Pn.
, двойственное исходному, причем его дифференциальные уравнения в тангенциальном репере (5)-(6) имеют вид (18), аналогичный уровнениям (I) H-распределения проективного пространства Pn.
Теорему 1 впервые доказал А.В. Столяров [6], [7] для гиперполосных распределений и для регулярных гиперполос, а также построил с помощью преобразования ![]() двойственные образы.
двойственные образы.
Отметим, что инволютивность преобразования ![]() (I) для частного класса трехсоставных распределений
(I) для частного класса трехсоставных распределений![]() доказана в работе [5], для скомпонованных S-распределений в работах [1], [2], для H-распределений в работе [3]. Двойственная теория имеет место и на оснащенном H-распределении в Pn.
доказана в работе [5], для скомпонованных S-распределений в работах [1], [2], для H-распределений в работе [3]. Двойственная теория имеет место и на оснащенном H-распределении в Pn.
Пусть основные структурные подрасслоения (L-подрасслоение, L-подрасслоение и Е-подрасслоение [4]) нормализованы в смысле Нордена соответственно полями квазитензоров![]() удовлетворяющими уравнениям
удовлетворяющими уравнениям
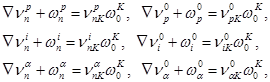 (19)
(19)
Легко убедиться, в силу соотношений (3), (I), (19), что функции
![]()
![]() (20)
(20)
![]()
удовлетворяют соответственно уравнениям
![]()
![]() (21)
(21)
![]()
где
![]()
![]()
![]()
Следовательно, всякая нормализация H–распределения индуцирует двойственную ей нормализацию. При этом оснащающие объекты связаны соотношениями (20), удовлетворяющими уравнениям (21).
Таким образом справедлива
Теорема 2 . Нормализация в смысле Нордена одного из регулярных трехсоставных распределений ![]() и
и ![]() равносильна нормализации другого, при этом компоненты полей оснащенных объектов связаны соотношениями (20).
равносильна нормализации другого, при этом компоненты полей оснащенных объектов связаны соотношениями (20).
В первых трех дифференциальных окрестностях в работе [4] построены (без применения теории двойственности) различные внутренние инвариантные нормализации H-распределения проективного пространства Pn. Таким образом, в силу теоремы 2 утверждаем: зная закон охвата объекта нормали первого (втрого) рода ![]() любого ассоциированного распределения с данным H-распределением, можно построить внутренним образом определенную соответствующую нормаль второго (первого) рода
любого ассоциированного распределения с данным H-распределением, можно построить внутренним образом определенную соответствующую нормаль второго (первого) рода ![]() данного ассоциированного распределения по следующей схеме [6],[7]. Построим охват квазитензора
данного ассоциированного распределения по следующей схеме [6],[7]. Построим охват квазитензора ![]() двойственного образа
двойственного образа![]() аналогичный охвату
аналогичный охвату![]() после чего, используя двойственные соотношения (например (7)—(17), (20)) находим соответствующую нормаль
после чего, используя двойственные соотношения (например (7)—(17), (20)) находим соответствующую нормаль![]() . В этом случае говорят [6], [7], что поля нормалей
. В этом случае говорят [6], [7], что поля нормалей![]() и
и![]() двойственны друг другу по отношению к инволютивному преобразованию
двойственны друг другу по отношению к инволютивному преобразованию ![]() (I).
(I).
§ 3. Аналитические признаки двойственности и H(L) и H(M) - подрасслоений,ассоциированных с H -распределением
Из формул (I.b) получаем соотношения:
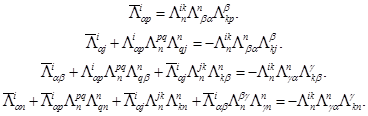 (III)
(III)
− − − − − − − − − − − − − − − − − − − − − − − − − − − − − −
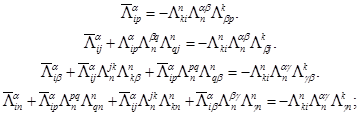 (IV)
(IV)
Известно [7], что инволютивное преобразование ![]()
![]() , заданное системой из
, заданное системой из ![]() форм Пфаффа
форм Пфаффа ![]() :
:
![]()
![]()
![]()
![]()
![]() (I*)
(I*)
![]()
![]()
![]()
преобразует гиперполосное распределение H(L) (H(L)-распределение) в двойственное ему гиперполосное распределение ![]() Если преобразование
Если преобразование ![]() (I) индуцирует преобразование
(I) индуцирует преобразование ![]() (I*), то выполняются условия
(I*), то выполняются условия
![]()
из которых согласно формулам (I) получим
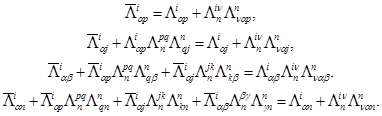 (V)
(V)
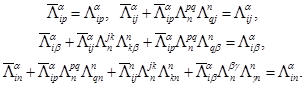 (VI)
(VI)
Нетрудно убедиться, что из соотношений (III) и (V) следуют условия
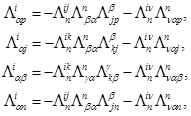 (VII)
(VII)
а из соотношений (IV) и (VI) соответственно условия
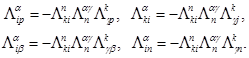 (VIII)
(VIII)
Условия (VII), (VIII) являются не только необходимым, но и достаточными, чтобы преобразование ![]() (I) порождало преобразование
(I) порождало преобразование ![]() (I*). Действительно, если выполняются соотношения (VII) и (VIII) для H-распределения, то из (VII) и (III) следуют (V), а из (VIII) и (IV) следуют (VI).
(I*). Действительно, если выполняются соотношения (VII) и (VIII) для H-распределения, то из (VII) и (III) следуют (V), а из (VIII) и (IV) следуют (VI).
Таким образом, доказана
Теорема 3.Для того, чтобы инволютивное преобразование ![]() (I) индуцировало инволютивное преобразование
(I) индуцировало инволютивное преобразование ![]() (I*) необходимо и достаточно, чтобы выполнялись условия (VII), (VIII).
(I*) необходимо и достаточно, чтобы выполнялись условия (VII), (VIII).
Геометрическая интерпретация теоремы 3 такова: инволютивное преобразование ![]() при условиях (VII), (VIII), не только преобразует трехсоставное распределение H в двойственный ему образ , но и ассоциированное с ним H(L)- распределение преобразует в двойственный ему образ
при условиях (VII), (VIII), не только преобразует трехсоставное распределение H в двойственный ему образ , но и ассоциированное с ним H(L)- распределение преобразует в двойственный ему образ ![]() .
.
3. Преобразуем формулы (I.c) соответственно следующим образом:
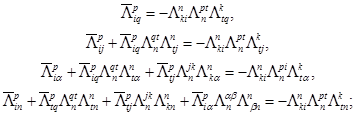 (IX)
(IX)
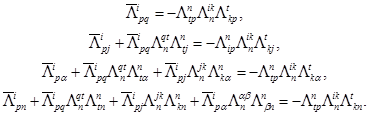 (X)
(X)
Аналогично, следуя работе [7], утверждаем, что инволютивное преобразование ![]()
![]() , заданное системой из форм Пфаффа
, заданное системой из форм Пфаффа
![]()
![]()
![]()
![]()
![]() (I*)
(I*)
![]()
![]()
![]()
преобразует гиперполосное распределение H(М) (H(М)-распределение) в
двойственное ему гиперполосное распределение ![]() . Пусть преобразование
. Пусть преобразование ![]() (I) индуцирует преобразование J(I*), тогда выполняются равенства
(I) индуцирует преобразование J(I*), тогда выполняются равенства
![]()
которые (в силу(I)) преобразуем, соответственно, в следующие соотношения:
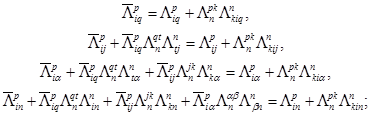 (XI)
(XI)
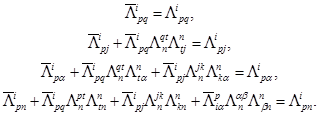 (XII)
(XII)
Теперь из соотношений (IX) и (XI) непосредственно получаем условия
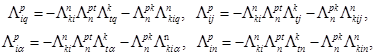 (XIII)
(XIII)
а из соотношений (X) и (XII) — условия
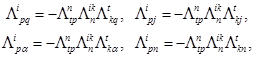 (XIV)
(XIV)
Соотношения (XIII), (XIV) являются не только необходимыми, но и достаточными условиями, чтобы преобразование ![]() (I) порождало инволютивное преобразование J(II*). Действительно, если выполняются соотношения (XIII), (XIV) для H-распределения, то из (XIII) и (IX) следуют соотношения (XI), а из (XIV) и (X) следуют соотношения (XII). Это означает, что преобразование
(I) порождало инволютивное преобразование J(II*). Действительно, если выполняются соотношения (XIII), (XIV) для H-распределения, то из (XIII) и (IX) следуют соотношения (XI), а из (XIV) и (X) следуют соотношения (XII). Это означает, что преобразование ![]() (I) порождает преобразование J(II*).
(I) порождает преобразование J(II*).
Итак, справедлива
Теорема 4. Для того, чтобы инволютивное преобразование ![]() (I) порождало инволютивное преобразование J(II*) необходимо и достаточно, чтобы выполнялись условия (XIII) и (XIV).
(I) порождало инволютивное преобразование J(II*) необходимо и достаточно, чтобы выполнялись условия (XIII) и (XIV).
Теорему 4 можно геометрически интерпретировать следующим образом: инволютивное преобразование ![]() при выполнении условий (XIII), (XIV) не только переводит трехсоставное распределение H в двойственный ему образ
при выполнении условий (XIII), (XIV) не только переводит трехсоставное распределение H в двойственный ему образ ![]() , но и ассоциированное с ним H(М)-распределение преобразует в двойственный образ
, но и ассоциированное с ним H(М)-распределение преобразует в двойственный образ ![]() .
.
Список литературы:
1.Волкова С.Ю. О двойственных проективных связностях H(L,L)- распределения. // Дифференциальная геометрия многообразий фигур. Калининград, Калинингр.ун-т, — 1993. — Вып. 24. — с. 28—37.
2.Волкова С.Ю. Двойственные аффинные и проективные связности S-распределения. /БВМИ. 2001. — 70 с. — Деп в ВИНИТИ РАН. — 15.08.01. — № 1871−В2001.
3.Елисеева А.В. H(П)-распределения проективного пространства // ВИНИТИ РАН. — 01.02.2002. — 49 с. — № 206-В2002Деп.
4.Попов Ю.И. Основы теории трехсоставных распределений проективного пространства. Монография. Санкт-Петербург. Из-во С-Петербургского ун-та, 1992. — 172 с.
5. Попов Ю.И. Трехсоставные регулярные распределения ![]() проективного пространства. Калининградский гос.ун-т. Калининград. 1982. — 126 с. — Деп в ВИНИТИ, № 6192-82Деп.
проективного пространства. Калининградский гос.ун-т. Калининград. 1982. — 126 с. — Деп в ВИНИТИ, № 6192-82Деп.
6.Столяров А.В. Двойственные нормальные связности на регулярной неголономной гиперполосе // Изв. НАНИ ЧР (физ.-мат. Науки). Чебоксары, — 1996. — № 6 — С. 9—14.
7.Столяров А.В. Двойственная теория оснащенных многообразий: Монография. 2-е изд. \ Чуваш.пед.ин-т. Чебоксары, 1994. — 290 с.
дипломов


Оставить комментарий